Основные элементы комбинаторики: перестановки, размещения, сочетания.

Основные элементы комбинаторики: перестановки, размещения, сочетания.

Пример 1. Набирая номер телефона, абонент забыл одну цифру и набрал ее наудачу. Найти вероятность того, что набрана нужная цифра.

Р е ш е н и е. Обозначим через А событие — набрана нужная цифра. Абонент мог набрать любую из 10 цифр, поэтому общее число возможных элементарных исходов равно 10. Эти исходы несовместны, равновозможны и образуют полную группу. Благоприятствует событию А лишь один исход (нужная цифра лишь одна). Искомая вероятность равна отношению числа исходов, благоприятствующих событию, к числу всех элементарных исходов:

Р (А) = 1 / 10.

Пример 2. Набирая номер телефона, абонент забыл последние две цифры и, помня лишь, что эти цифры различны, набрал их наудачу. Найти вероятность того, что набраны нужные цифры.

Р е ш е н и е. Обозначим через В событие — набраны две нужные цифры. Всего можно набрать столько различных цифр, сколько может быть составлено размещений из десяти цифр по две, т. е. A²₁₀ = 10 * 9 = 90. Таким образом, общее число возможных элементарных исходов равно 90. Эти исходы несовместны, равновозможны и образуют полную группу. Благоприятствует событию В лишь один исход. Искомая вероятность равна отношению числа исходов, благоприятствующих событию, к числу всех элементарных исходов:

Р (В) = 1 / 90.

Пример 3. Указать ошибку "решения" задачи: "Брошены две игральные кости. Найти вероятность того, что сумма выпавших очков равна 4 (событие A)".

Р е ш е н и е. Всего возможны 2 исхода испытания: сумма выпавших очков равна 4, сумма выпавших очков не равна 4. Событию А благоприятствует один исход: общее число исходов равно двум. Следовательно, искомая вероятность

P (A) = 1 / 2.

Ошибка этого решения состоит в том, что рассматриваемые исходы не являются равновозможными.

П р а в и л ь н о е р е ш е н и е. Общее число равновозможных исходов испытания равно 6 * 6 = 36 (каждое число выпавших очков на одной кости может сочетаться со всеми числами очков другой кости). Среди этих исходов благоприятствуют событию А только 3 исхода: (1; 3), (3; 1), (2; 2) (в скобках указаны числа выпавших очков). Следовательно, искомая вероятность

Р (A) = 3 / 36 = 1 / 12.

Пример 4. В партии из 10 деталей 7 стандартных. Найти вероятность того, что среди шести взятых наудачу деталей 4 стандартных.

Р е ш е н и е. Общее число возможных элементарных исходов испытания равно числу способов, которыми можно извлечь 6 деталей из 10, т.е. числу сочетаний из 10 элементов по 6 элементов (С⁶₁₀).

Определим число исходов, благоприятствующих интересующему нас событию А (среди шести взятых деталей 4 стандартных). Четыре стандартные детали можно взять из семи стандартных деталей C⁴₇ способами; при этом остальные 6 - 4 = 2 детали должны быть нестандартными; взять же 2 нестандартные детали из 10 - 7 = 3 нестандартных деталей можно С²₃ способами. Следовательно, число благоприятствующих исходов равно C⁴₇ * C²₃.

Искомая вероятность равна отношению числа исходов, благоприятствующих событию, к числу всех элементарных исходов:

P (A) = (C⁴₇ * C²₃) / C⁶₁₀ = 1 / 2.

Теорема сложения вероятностей для несовместных событий.

Вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий:

Р (А + В) = Р (А) + Р (В).

Пример 1. В урне 30 шаров: 10 красных, 5 синих и 15 белых. Найти вероятность появления цветного шара.

Р е ш е н и е. Появление цветного шара означает появление либо красного, либо синего шара.

Вероятность появления красного шара (событие А)

Р (А) = 10 / 30 = 1 / 3.

Вероятность появления синего шара (событие В)

Р (В) = 5 / 30 = 1 / 6.

События А и В несовместны (появление шара одного цвета исключает появление шара другого цвета), поэтому теорема сложения применима.

Искомая вероятность

P (A + B) = P (A) + P (B) = l / 3 + l / 6 = l / 2.

Пример 2. Стрелок стреляет по мишени, разделенной на 3 области. Вероятность попадания в первую область равна 0,45, во вторую — 0,35. Найти вероятность того, что стрелок при одном выстреле попадет либо в первую, либо во вторую область.

Р е ш е н и е. События А — "стрелок попал в первую область" и В — "стрелок попал во вторую область" — несовместны (попадание в одну область исключает попадание в другую), поэтому теорема сложения применима.

Искомая вероятность

Р (А + В) = Р (А) + Р (В) = 0,45 + 0,35 = 0,80.

Решение.

Пусть А – попадание первого стрелка, ;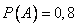

В – попадание второго стрелка, .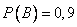

Тогда 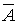- промах первого, ;

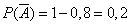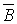- промах второго, .

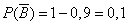Найдем нужные вероятности.

а) АВ – двойное попадание,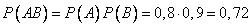

б) 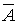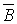– двойной промах, .

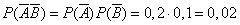в) А+В – хотя бы одно попадание,

.

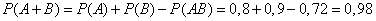г) 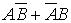– одно попадание,

.

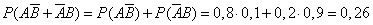Пример. Студент разыскивает нужную ему формулу в трех справочниках. Вероятности того, что формула содержится в первом, втором и третьем справочниках равны 0,6; 0,7 и 0,8. Найти вероятности того, что формула содержится 1) только в одном справочнике; 2) только в двух справочниках; 3) во всех трех справочниках.

Решение.

А – формула содержится в первом справочнике;

В – формула содержится во втором справочнике;

С – формула содержится в третьем справочнике.

Воспользуемся теоремами сложения и умножения вероятностей.

1.

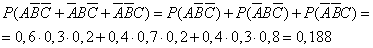
2. .

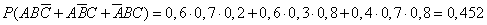3.

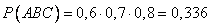
Пусть в результате испытания могут появиться n событий, независимых в совокупности, либо некоторые из них (в частности, только одно или ни одного), причем вероятности появления каждого из событий известны. Как найти вероятность того, что наступит хотя бы одно из этих событий? Например, если в результате испытания могут появиться три события, то появление хотя бы одного из этих событий означает наступление либо одного, либо двух, либо трех событий. Ответ на поставленный вопрос дает следующая теорема.

Теорема. Вероятность появления хотя бы одного из событий 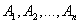, независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий

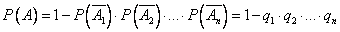
Если события 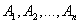имеют одинаковую вероятность 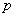, то формула принимает простой вид:

.

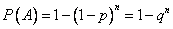Пример. Вероятности попадания в цель при стрельбе из трех орудий таковы: p1 = 0,8; p2 = 0,7; p3 = 0,9. Найти вероятность хотя бы одного попадания (событие А) при одном залпе из всех орудий.

Решение. Вероятность попадания в цель каждым из орудий не зависит от результатов стрельбы из других орудий, поэтому рассматриваемые события 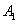(попадание первого орудия), 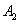(попадание второго орудия) и 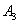(попадание третьего орудия) независимы в совокупности.

Вероятности событий, противоположных событиям 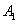, 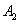и 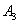(т. е. вероятности промахов), соответственно равны:

, ,

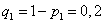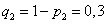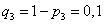
Искомая вероятность .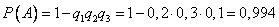

Пример. В типографии имеется 4 плоскопечатных машины. Для каждой машины вероятность того, что она работает в данный момент, равна 0,9. Найти вероятность того, что в данный момент работает хотя бы одна машина (событие А).

Решение. События "машина работает" и "машина не работает" (в данный момент) — противоположные, поэтому сумма их вероятностей равна единице: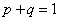

Отсюда вероятность того, что машина в данный момент не работает, равна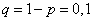

Искомая вероятность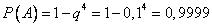

Так как полученная вероятность весьма близка к единице, то на основании следствия из принципа практической невозможности маловероятных событий мы вправе заключить, что в данный момент работает хотя бы одна из машин.

Пример. Вероятность того, что при одном выстреле стрелок попадает в цель, равна 0,4. Сколько выстрелов должен произвести стрелок, чтобы с вероятностью не менее 0,9 он попал в цель хотя бы один раз?

Решение. Обозначим через А событие "при n выстрелах стрелок попадает в цель хотя бы один раз". События, состоящие в попадании в цель при первом, втором выстрелах и т. д., независимы в совокупности, поэтому применима формула .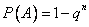

Приняв во внимание, что, по условию, 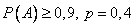(следовательно, 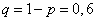), получим

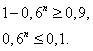
Прологарифмируем это неравенство по основанию 10:

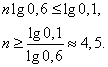
Итак, 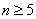, т.е. стрелок должен произвести не менее 5 выстрелов.

Формула полной вероятности.

События образуют полную группу, если они в совокупности описывают все возможные несовместные друг с другом исходы некоторого испытания; сумма вероятностей событий полной группы равна 1. Например, испытание - бросание игральной кости. Всего исходов испытания - шесть (число выпавших очков от 1 до 6), каждый может произойти с вероятностью 1/6, сумма вероятностей всех исходов равна 1.
Предположим, что событие A может наступить лишь при появлении одного из несовместных событий (гипотез) H₁, H₂, ..., H_n, образующих полную группу. Тогда вероятность события A определяется как сумма произведений вероятностей каждой из гипотез на соответствующую условную вероятность события A:

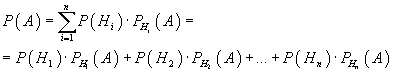
В каждой из двух урн находится 9 белых и 14 чёрных шаров. Из первой урны во вторую переложили наудачу один шар, а затем из второй урны вынули наудачу один шар. Найти вероятность того, что шар, вынутый из второй урны, окажется чёрным.

Решение
Событие А - шар, вынутый из второй урны, оказался чёрным.
Гипотеза Н₁ - из первой урны во вторую переложили белый шар. Р(Н₁) = 9/23.
Гипотеза Н₂ - из первой урны во вторую переложили чёрный шар. Р(Н₂) = 14/23.
После перекладывания во второй урне стало 24 шара. Условные вероятности события А:

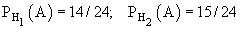
По формуле полной вероятности

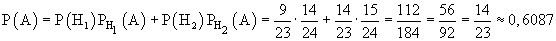
Пример. В магазин поступила новая продукция с трех предприятий. Процентный состав этой продукции следующий: 20% - продукция первого предприятия, 30% - продукция второго предприятия, 50% - продукция третьего предприятия; далее, 10% продукции первого предприятия высшего сорта, на втором предприятии - 5% и на третьем - 20% продукции высшего сорта. Найти вероятность того, что случайно купленная новая продукция окажется высшего сорта.

Решение. Обозначим через В событие, заключающееся в том, что будет куплена продукция высшего сорта, через 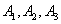обозначим события, заключающиеся в покупке продукции, принадлежащей соответственно первому, второму и третьему предприятиям.

Можно применить формулу полной вероятности, причем в наших обозначениях:

Подставляя эти значения в формулу полной вероятности, получим искомую вероятность:

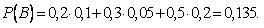
Теорема гипотез (формула Байеса).

Пример. Один из трех стрелков вызывается на линию огня и производит два выстрела. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,3, для второго - 0,5; для третьего - 0,8. Мишень не поражена. Найти вероятность того, что выстрелы произведены первым стрелком.

Решение. Возможны три гипотезы:

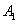- на линию огня вызван первый стрелок,

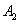- на линию огня вызван второй стрелок,

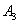- на линию огня вызван третий стрелок.

Так как вызов на линию огня любого стрелка равновозможен, то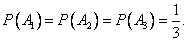

В результате опыта наблюдалось событие В - после произведенных выстрелов мишень не поражена. Условные вероятности этого события при сделанных гипотезах равны:

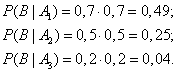
по формуле Байеса находим вероятность гипотезы 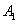после опыта:

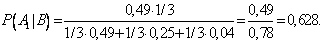
Два цеха штампуют однотипные детали. Первый цех дает 5% брака, второй - 4%. Для контроля отобрано 20 деталей с первого цеха и 10 деталей со второго. Эти детали смешаны в одну партию, и из нее наудачу извлекают одну деталь. Деталь оказалась бракованная. Какова вероятность того, что она из цеха №1?

Решение
Событие А – деталь оказалась бракованной.
Гипотеза Н₁ – деталь изготовлена в 1-м цехе; Р(Н₁) = 2/3
Гипотеза Н₂ – деталь изготовлена во 2-м цехе; Р(Н₂) = 1/3
Условные вероятности события А: P_H1(A)=0,05; P_H2(A)=0,04
Требуется найти вероятность первой гипотезы в предположении, что событие А уже произошло:
P_A(H₁) - ?
Используем формулу вероятности гипотез Бейеса, подставив в знаменатель формулу полной вероятности:

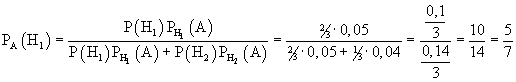
Основные элементы комбинаторики: перестановки, размещения, сочетания.

Пример 1. Набирая номер телефона, абонент забыл одну цифру и набрал ее наудачу. Найти вероятность того, что набрана нужная цифра.

Р е ш е н и е. Обозначим через А событие — набрана нужная цифра. Абонент мог набрать любую из 10 цифр, поэтому общее число возможных элементарных исходов равно 10. Эти исходы несовместны, равновозможны и образуют полную группу. Благоприятствует событию А лишь один исход (нужная цифра лишь одна). Искомая вероятность равна отношению числа исходов, благоприятствующих событию, к числу всех элементарных исходов:

Р (А) = 1 / 10.

Пример 2. Набирая номер телефона, абонент забыл последние две цифры и, помня лишь, что эти цифры различны, набрал их наудачу. Найти вероятность того, что набраны нужные цифры.

Р е ш е н и е. Обозначим через В событие — набраны две нужные цифры. Всего можно набрать столько различных цифр, сколько может быть составлено размещений из десяти цифр по две, т. е. A²₁₀ = 10 * 9 = 90. Таким образом, общее число возможных элементарных исходов равно 90. Эти исходы несовместны, равновозможны и образуют полную группу. Благоприятствует событию В лишь один исход. Искомая вероятность равна отношению числа исходов, благоприятствующих событию, к числу всех элементарных исходов:

Р (В) = 1 / 90.

Пример 3. Указать ошибку "решения" задачи: "Брошены две игральные кости. Найти вероятность того, что сумма выпавших очков равна 4 (событие A)".

Р е ш е н и е. Всего возможны 2 исхода испытания: сумма выпавших очков равна 4, сумма выпавших очков не равна 4. Событию А благоприятствует один исход: общее число исходов равно двум. Следовательно, искомая вероятность

P (A) = 1 / 2.

Ошибка этого решения состоит в том, что рассматриваемые исходы не являются равновозможными.

П р а в и л ь н о е р е ш е н и е. Общее число равновозможных исходов испытания равно 6 * 6 = 36 (каждое число выпавших очков на одной кости может сочетаться со всеми числами очков другой кости). Среди этих исходов благоприятствуют событию А только 3 исхода: (1; 3), (3; 1), (2; 2) (в скобках указаны числа выпавших очков). Следовательно, искомая вероятность

Р (A) = 3 / 36 = 1 / 12.

Пример 4. В партии из 10 деталей 7 стандартных. Найти вероятность того, что среди шести взятых наудачу деталей 4 стандартных.

Р е ш е н и е. Общее число возможных элементарных исходов испытания равно числу способов, которыми можно извлечь 6 деталей из 10, т.е. числу сочетаний из 10 элементов по 6 элементов (С⁶₁₀).

Определим число исходов, благоприятствующих интересующему нас событию А (среди шести взятых деталей 4 стандартных). Четыре стандартные детали можно взять из семи стандартных деталей C⁴₇ способами; при этом остальные 6 - 4 = 2 детали должны быть нестандартными; взять же 2 нестандартные детали из 10 - 7 = 3 нестандартных деталей можно С²₃ способами. Следовательно, число благоприятствующих исходов равно C⁴₇ * C²₃.

Искомая вероятность равна отношению числа исходов, благоприятствующих событию, к числу всех элементарных исходов:

P (A) = (C⁴₇ * C²₃) / C⁶₁₀ = 1 / 2.

Теорема сложения вероятностей для несовместных событий.

Вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий:

Р (А + В) = Р (А) + Р (В).

Пример 1. В урне 30 шаров: 10 красных, 5 синих и 15 белых. Найти вероятность появления цветного шара.

Р е ш е н и е. Появление цветного шара означает появление либо красного, либо синего шара.

Вероятность появления красного шара (событие А)

Р (А) = 10 / 30 = 1 / 3.

Вероятность появления синего шара (событие В)

Р (В) = 5 / 30 = 1 / 6.

События А и В несовместны (появление шара одного цвета исключает появление шара другого цвета), поэтому теорема сложения применима.

Искомая вероятность

P (A + B) = P (A) + P (B) = l / 3 + l / 6 = l / 2.

Пример 2. Стрелок стреляет по мишени, разделенной на 3 области. Вероятность попадания в первую область равна 0,45, во вторую — 0,35. Найти вероятность того, что стрелок при одном выстреле попадет либо в первую, либо во вторую область.

Р е ш е н и е. События А — "стрелок попал в первую область" и В — "стрелок попал во вторую область" — несовместны (попадание в одну область исключает попадание в другую), поэтому теорема сложения применима.

Искомая вероятность

Р (А + В) = Р (А) + Р (В) = 0,45 + 0,35 = 0,80.