Проверка сложной гипотезы об интерквантильном промежутке
Непрерывная случайная величина xобразует генеральную совокупностьX, на которой определены вероятностная мера и плотность распределения 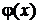 . Вид плотности распределения произвольный. Из генеральной совокупности извлечена выборка
. Вид плотности распределения произвольный. Из генеральной совокупности извлечена выборка  объема
объема 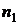 .
.
Заданы допускаемые пределы  , внутри которых должен находиться генеральный интерквантильный промежуток
, внутри которых должен находиться генеральный интерквантильный промежуток 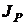 , содержащий не менее
, содержащий не менее  значений этой генеральной совокупности. Это означает, что в силу монотонности вероятностная мера интервала
значений этой генеральной совокупности. Это означает, что в силу монотонности вероятностная мера интервала  , которая определена на генеральной совокупности X, не должна быть меньше, чем
, которая определена на генеральной совокупности X, не должна быть меньше, чем  , поскольку предполагаемый интерквантильный промежуток вложен в этот интервал. Поэтому гипотеза об интерквантильном промежутке
, поскольку предполагаемый интерквантильный промежуток вложен в этот интервал. Поэтому гипотеза об интерквантильном промежутке
 :
:  против альтернативы
против альтернативы  :
: 
эквивалентна гипотезе
 :
:  против альтернативы
против альтернативы
 :
:  ,
,
то есть гипотезе о вероятности
 : p ³
: p ³  против альтернативы
против альтернативы  : p <
: p <  .
.
Заданы вероятности ошибок первого и второго рода a и b.
Гипотезы такого рода проверяются при испытаниях продукции, на характеристики которых установлены пределы допускаемых отклонений от номинальных значений, объявленных на этикетках, в документах или в рекламе.
Естественной статистикой для проверки этой гипотезы является оценка вероятности в соответствии с ее частотным определением:
 ,
,
где 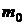 – количество выборочных значений, попавших в интервал
– количество выборочных значений, попавших в интервал  , n – объем выборки.
, n – объем выборки.
Излагаемый метод проверки сформулированной гипотезы относится к distribution-free методам, то есть к методам, которые в отличие от предыдущих, пригодных только при нормальном распределении, не зависят от вида плотности распределения.
Будем использовать подход, который применялся в предыдущих пунктах. Для этого необходимо определить границы доверительного интервала для вероятности. В соответствии с разд. 2.4.2 и заданными вероятностями ошибочных решений a и bграницы доверительного интервала для вероятности определяются из уравнений:
нижняя граница
 ;
;
верхняя граница
 .
.

На рис. 41 показаны варианты расположения доверительного интервала для вероятности относительно зон, соответствующих гипотезам  и
и  . В соответствии с формулировкой гипотезы и в связи с тем, что
. В соответствии с формулировкой гипотезы и в связи с тем, что  , положение верхней границы доверительного интервала в зоне, соответствующей гипотезе
, положение верхней границы доверительного интервала в зоне, соответствующей гипотезе  , безразлично. По указанным причинам для этого варианта строится доверительный интервал, верхняя граница которого равна 1, а нижняя граница определяется заданной вероятностью b ошибки второго рода:
, безразлично. По указанным причинам для этого варианта строится доверительный интервал, верхняя граница которого равна 1, а нижняя граница определяется заданной вероятностью b ошибки второго рода:
 .
.
Таким образом, решение о справедливости гипотезы  принимается, когда нижняя граница доверительного интервала для вероятности оказывается больше заданного значения
принимается, когда нижняя граница доверительного интервала для вероятности оказывается больше заданного значения  , то есть когда
, то есть когда
 .
.
В данной ситуации вероятность того, что истинное значение вероятности находится в зоне, соответствующей гипотезе  , не превышает b, поскольку в данной ситуации
, не превышает b, поскольку в данной ситуации  , значит, в силу монотонности вероятностной меры
, значит, в силу монотонности вероятностной меры  .
.
Из этого следует, что вероятность ошибки второго рода  .
.
В соответствии с формулировкой гипотезы и поскольку  положение нижней границы доверительного интервала в зоне, соответствующей гипотезе
положение нижней границы доверительного интервала в зоне, соответствующей гипотезе  , безразлично. В связи с этим здесь строится доверительный интервал, нижняя граница которого равна 0, а верхняя граница определяется заданной вероятностью a ошибки первого рода:
, безразлично. В связи с этим здесь строится доверительный интервал, нижняя граница которого равна 0, а верхняя граница определяется заданной вероятностью a ошибки первого рода:
 .
.
Решение об отклонении нулевой гипотезы принимается, когда верхняя граница доверительного интервала для вероятности меньше заданного значения  , то есть когда
, то есть когда
 <
<  .
.
Вероятность ошибки в этом решении не превышает заданного значения a, поскольку в данной ситуации  ; значит, в силу монотонности вероятностной меры
; значит, в силу монотонности вероятностной меры  .
.
Из этого следует, что вероятность ошибки первого рода  .
.
В третьем варианте, показанном на рис. 41, в), не имеется достаточных оснований для принятия никакого иного решения, кроме решения продолжить испытания с целью увеличения объема выборки. Надежда здесь возлагается на то, что с увеличением объема выборки ширина доверительного интервала уменьшается.
После увеличения объема выборки до  снова строятся доверительные интервалы при тех же заданных значениях вероятностей a и b, и на втором этапе вновь возможны три варианта расположения нового, более узкого доверительного интервала относительно значения
снова строятся доверительные интервалы при тех же заданных значениях вероятностей a и b, и на втором этапе вновь возможны три варианта расположения нового, более узкого доверительного интервала относительно значения  . Все описанные рассуждения и действия повторяются.
. Все описанные рассуждения и действия повторяются.
В конечном итоге описанная последовательная процедура проверки сложной гипотезы о вероятности должна завершиться выходом доверительного интервала целиком в одну из зон и принятием соответствующей гипотезы. Когда по экономическим, техническим и иным причинам дальнейшее продолжение испытаний (экспериментов) оказывается невозможным, придется принимать произвольное (так называемое волевое) решение об отклонении той или иной гипотезы в зависимости от того, какого рода риск (первого или второго) более оправдан.
Удобным для практического применения может быть иной метод проверки сложной гипотезы о вероятности, а именно, метод статистического последовательного анализа А. Вальда [8,9], которому посвящен отдельный раздел 2.7.6.
