Проверка сложной гипотезы о дисперсии

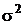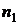Плотность распределения генеральной совокупности X нормальна, дисперсия неизвестна. Из генеральной совокупности извлечена выборка объема . Проверяется сложная гипотеза:

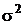: £ d против альтернативы : 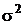> d.

Заданы вероятности ошибок первого и второго рода a и b.

Естественной статистикой для проверки гипотезы о дисперсии является ее несмещенная оценка:

.

Доверительный интервал для дисперсии определен в разд. 2.4.5 следующим образом:

.

На рис. 40 показаны варианты расположения доверительного интервала для дисперсии относительно зон, соответствующих гипотезам и . В соответствии с формулировкой гипотезы и в связи с тем, что , положение нижней границы доверительного интервала в зоне, соответствующей гипотезе , безразлично. По указанным причинам для этого варианта строится доверительный интервал, нижняя граница которого равна 0, а верхняя граница определяется заданной вероятностью b ошибки второго рода:

где – -процентная квантиль плотности распределения хи-квадрат.

Таким образом, решение о принятии гипотезы принимается, когда верхняя граница доверительного интервала для дисперсии оказывается меньше заданного значения d, то есть когда

.

В данной ситуации вероятность того, что истинное значение дисперсии находится в зоне, соответствующей гипотезе , не превышает b, поскольку в данной ситуации

,

значит, в силу монотонности вероятностной меры

.

Из этого следует, что вероятность ошибки второго рода .

В соответствии с формулировкой гипотезы положение верхней границы доверительного интервала в зоне, соответствующей гипотезе , безразлично. В связи с этим здесь строится доверительный интервал, верхняя граница которого равна ¥, а нижняя граница определяется заданной вероятностью a ошибки первого рода:

где – -процентная квантиль плотности распределения хи-квадрат.

Решение об отклонении нулевой гипотезы принимается, когда нижняя граница доверительного интервала для дисперсии превышает заданное значение d, то есть когда

.

Вероятность ошибки в этом решении не превышает заданного значения a, поскольку в данной ситуации

,

значит, в силу монотонности вероятностной меры

.

Из этого следует, что вероятность ошибки первого рода .

В третьем варианте, показанном на рис. 40, в), не имеется достаточных оснований для принятия никакого иного решения, кроме решения продолжить испытания с целью увеличения объема выборки. Надежда здесь возлагается на то, что с увеличением объема выборки ширина доверительного интервала уменьшается.

После увеличения объема выборки до 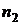снова строится доверительный интервал при тех же заданных значениях вероятностей a и b, и на втором этапе вновь возможны три варианта расположения нового, более узкого доверительного интервала относительно значения d. Все описанные рассуждения и действия повторяются.

В конечном итоге описанная последовательная процедура проверки сложной гипотезы о дисперсии должна завершиться выходом доверительного интервала целиком в одну из зон и принятием соответствующей гипотезы. Когда по экономическим, техническим и иным причинам дальнейшее продолжение испытаний (экспериментов) оказывается невозможным, придется принимать решение об отклонении той или иной гипотезы в зависимости от того, какого рода риск (первого или второго) более оправдан.