Критические значения критерия Колмогорова – Смирнова

α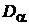
0,2	0,208	0,148	0,118	0,106
0,1	0,238	0,169	0,135	0,121
0,05	0,264	0,188	0,150	0,134

Если n > 10 и вероятность a выражена в относительных единицах, для расчета критических значений можно пользоваться приближенной формулой

.

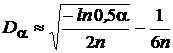П р о ц е д у р а п р о в е р к и г и п о т е з ы о в и д е ф у н к ц и и р а с п р е д е л е н и я по критерию Колмогорова-Смирнова.

1. Задается уровень значимости a.

2. По выборочным данным строят выборочную функцию распределения в соответствии с указаниями разд. 2.2.

3. Вычисляют точечные оценки моментов.

4. Из теоретических соображений, по виду выборочной функции распределения, по соотношениям между моментами, по значениям асимметрии и эксцесса, по результатам анализа других данных выдвигается гипотеза о виде функции распределения 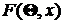и тем самым – о виде плотности распределения .

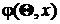5. Вычисляют r параметров предполагаемой функции распределения и ее значения 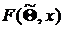при .

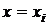6. Вычисляют статистику критерия .

7. Полученное значение сравнивают с критическим значением .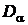

8. Если 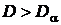делают вывод о том, что экспериментальные данные не подтверждают справедливость выдвинутой гипотезы или о том, что отсутствуют достаточные основания для того, чтобы считать нулевую гипотезу справедливой. Гипотезу пересматривают, выдвигают новую нулевую гипотезу и переходят на п. 4 данной процедуры.

9. Если 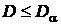делают вывод о том, что экспериментальные данные не противоречат выдвинутой гипотезе или о том, что имеются достаточные основания для того, чтобы считать нулевую гипотезу справедливой.

Условие корректного применения критерия Колмогорова – Смирнова: исходная выборка 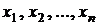делится на две части. По одной из них определяют параметры 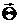, по другой – строят выборочную функцию распределения и вычисляют статистику критерия. Это позволяет избавиться от необходимости учета зависимости между выборочными значениями, которая появляется в результате вычисления параметров предполагаемой плотности распределения и соответствующего уменьшения числа степеней свободы, как это было при использовании критерия .

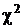2.5.5.3. Критерий 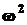Мизеса

Из генеральной совокупности X,образованной случайной величиной x, извлечена выборка 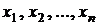. Выдвигается предположение о том, что функция распределения случайной величины есть 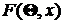, где 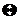– вектор параметров. По выборочным данным вычисляют оценки параметров 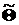и проверяют сложную гипотезу

: функция распределения случайной величины x есть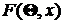

против альтернативы

: функция распределения случайной величины xне .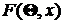

Поскольку эта гипотеза сложная, задают только вероятность ошибки первого рода a, которая в подобных случаях именуется уровнем значимости.

В соответствии с формулировкой гипотезы сравнивают две функции распределения: выборочную (разд. 2.2) и предполагаемую. Различие между ними определено, как

,

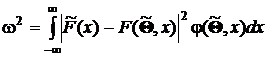где 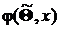– предполагаемая плотность распределения.

Этот интеграл вычисляется как сумма интегралов по интервалам между соседними членами вариационного ряда. Если на этих интервалах предполагаемая функция распределения интерполируется прямой линией, то этот интеграл выражается суммой

.

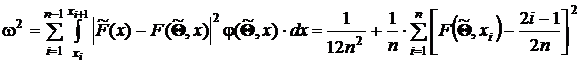В качестве статистики критерия используется

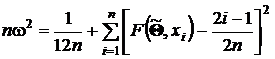
Критические значения 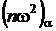приведены в таблицах математической статистики (см., например, [13,14]). В табл. 7 представлены некоторые часто употребляемые критические значения.

Таблица 7

Критические значения критерия 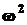Мизеса

a	0,03	0,05	0,1	0,2
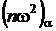	0,55	0,4614	0,3473	0,2415

П р о ц е д у р а п р о в е р к и г и п о т е з ы о в и д е ф у н к ц и и р а с п р е д е л е н и я по критерию 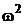Мизеса.

1. Задают уровень значимости a

2. По выборочным данным строят выборочную функцию распределения в соответствии с указаниями разд. 2.2

3. Вычисляют точечные оценки моментов.

4. Из теоретических соображений, по виду выборочной функции распределения, по соотношениям между моментами, по значениям асимметрии и эксцесса, по результатам анализа других данных выдвигается гипотеза о виде функции распределения 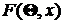и тем самым – о виде плотности распределения .

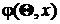5. Вычисляют r параметров предполагаемой функции распределения и ее значения 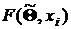при ,.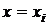

6. Вычисляют статистику критерия

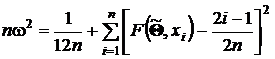
7. Полученное значение сравнивают с критическим значением .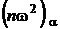

8. Если 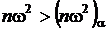делают вывод о том, что экспериментальные данные не подтверждают справедливость выдвинутой гипотезы, или о том, что отсутствуют достаточные основания для того, чтобы считать нулевую гипотезу справедливой. Гипотеза пересматривается, выдвигается новая нулевая гипотеза и выполняется переход на п. 4 данной процедуры.

9. Если 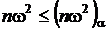, делают вывод о том, что экспериментальные данные подтверждают справедливость выдвинутой гипотезы, или о том, что имеются достаточные основания для того, чтобы считать нулевую гипотезу справедливой.

Критерий 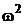Мизеса – равномерно наиболее мощный критерий проверки гипотезы о виде функции распределения.