Дифференциальная (относительная) энтропия

Пусть 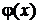– плотность распределения непрерывной случайной величины x. Воспользуемся выражением для энтропии, введенное выше в разд. 1.5:

,

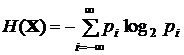где в качестве 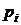будем использовать вероятностные меры интервалов одинаковой ширины .

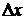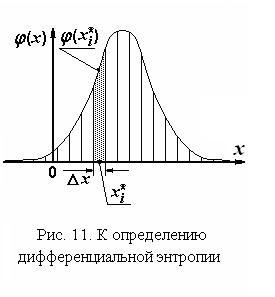
Каждая из этих вероятностных мер численно равна площади полосы шириной 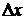, вырезанной из фигуры, ограниченной плотностью распределения и осью абсцисс, как это показано на рис. 11.

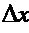По теореме о среднем, эта вероятностная мера равна площади прямоугольника, равновеликого заштрихованной криволинейной трапеции. Основание этого прямоугольника , высота его равна 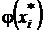, то есть плотности распределения в некоторой средней точке 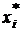. Тогда

,

.

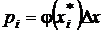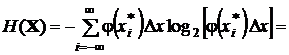
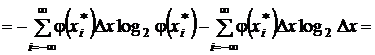
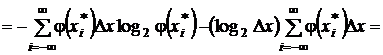
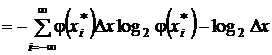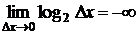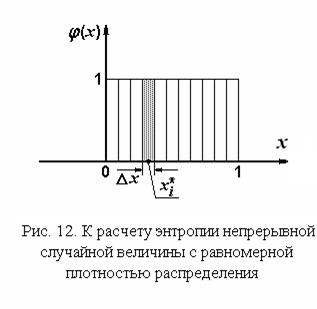
Теперь для получения окончательного решения необходимо совершить предельный переход при Dx ® 0. Однако из-за того, что , предел 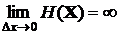. Этого следовало ожидать, поскольку непрерывная случайная величина на любом сколь угодно малом отрезке может принимать бесчисленное множество значений, и в отличие от дискретной величины все ее значения образуют более чем счетное множество. Мера неопределенности такого ансамбля не может быть меньше бесконечности вне зависимости от вида плотности распределения. Для того чтобы, несмотря на это обстоятельство, получить возможность сопоставления непрерывных случайных величин по значению энтропии, условились отсчитывать энтропию непрерывной случайной величины от некоторого уровня, который принимается за нуль. В качестве такого нулевого отсчета энтропии непрерывной случайной величины используется энтропия другой непрерывной случайной величины, плотность распределения которой равномерна на интервале (0, 1). График этой плотности распределения представлен на рис. 12. Ее аналитическая запись имеет вид

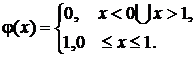
Как и ранее, ,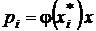

,

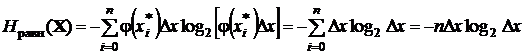где 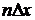= 1. С учетом этого равенства

.

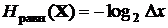Энтропия этой случайной величины в пределе при Dx ® 0 также стремится к бесконечности, но принимая эту энтропию за начало отсчета, определим относительную (дифференциальную) энтропию непрерывной случайной величины, как предел разности:

.

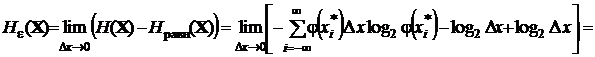
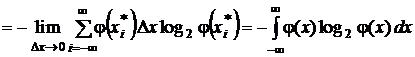Итак, относительная, или дифференциальная энтропия отсчитывается от энтропии случайной величины, распределенной равномерно на интервале (0, 1], поэтому она может быть отрицательной. Выпишем отдельно формулу, которая определяет относительную энтропию:

.

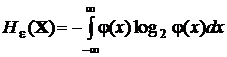Характеристическая функция непрерывной

Случайной величины

Характеристической функцией непрерывной случайной величины x называется математическое ожидание случайной функции 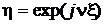(см., например, [3, 4]):

.

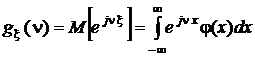Иными словами, характеристическая функция случайной величины есть интегральное преобразование плотности распределения этой случайной величины. Это преобразование – частный случай применения обратного преобразования Фурье к функциям, обладающим специфическими свойствами, присущими плотности распределения, а именно к неотрицательным функциям, интеграл от которых по всему множеству их определения равен 1. Отсюда следует, что характеристическая функция и плотность распределения связаны взаимно однозначно, то есть

.

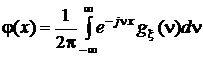Приведем несколько полезных свойств характеристической функции, первое из которых порождено спецификой плотности распределения случайной величины.

a) При n = 0

,

,

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

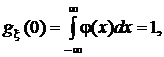
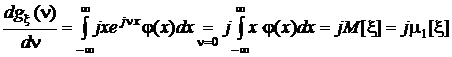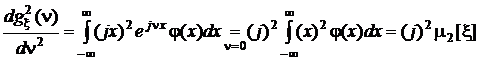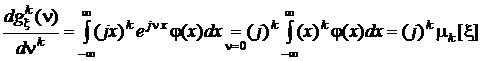Эти равенства означают, что для определения начальных моментов всех порядков достаточно знать выражение для характеристической функции, продифференцировать его k раз по аргументу n, подставить в полученную производную значение n = 0и разделить результат на 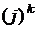. В частности, если необходимо определить дисперсию, то придется найти первый и второй начальные моменты и затем воспользоваться соотношением, которое было получено в разд. 1.3.3:

.

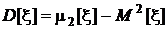б) Если задана случайная величина h, которая является линейной функцией случайной величины x:h = ax + b, то характеристическая функция случайной величины h есть

.

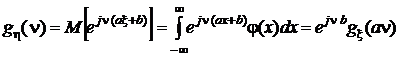Это свойство, в частности, означает, что при простом смещении значений случайной величины по оси абсцисс на величину b характеристическая функция умножается на экспоненту в степени jnb : если h = x + b,то .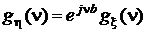

в) Пусть имеется последовательность 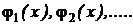плотностей распределения непрерывных случайных величин. Пусть 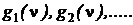– характеристические функции этих случайных величин. Если последовательность плотностей распределения сходится и предельная плотность распределения j(x),то последовательность характеристических функций также сходится и имеет предельную функцию g(n), которая есть характеристическая функция случайной величины с предельной плотностью распределения j(x). Иными словами, из сходимости плотностей распределения случайных величин следует сходимость их характеристических функций. Справедливо и обратное утверждение: из сходимости характеристических функций случайных величин следует сходимость их плотностей распределений.

Это свойство очевидным образом следует из взаимно однозначной связи между характеристическими функциями и плотностями распределения.

Необходимые условия того, чтобы некоторая функция g(n)была характеристической функцией:

g(n)непрерывна поn;

g(n) определена на каждом конечном интервалеn;

g(0) = 1;

|g(n)| £ 1.