П.2. Теоремы умножения вероятностей
Определение 1.Событие А называется независимым от события В, если вероятность события А не зависит от того, произошло событие В или нет.
Определение 2.Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет.
Примеры: 1) А = {появление решки на первой монете}, В = {появление решки на второй монете}. А и В – независимы.
2) А = {рождение мальчика у Тани}, В = {Рождение мальчика у Лены}. А и В – независимы.
3) В урне 2 белых и 1 черный шар. Двое Таня и Ваня вынимают из урны по одному шару. Зависимы или независимы события: А = {появление белого шара у Тани}, В = {появление белого шара у Вани}?
Решение.
Найдем вероятности событий. Р(А) = 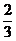 до известия о событии В. После известия о событии В данная вероятность Р(А) =
до известия о событии В. После известия о событии В данная вероятность Р(А) = 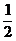 . Следовательно, А и В зависимые.
. Следовательно, А и В зависимые.
Определение 3.Два события называются независимыми, если появление одного из них не изменяет вероятности появления другого.
Определение 4.Несколько событий называются независимыми, если любое из них не зависит от любой совокупности остальных.
Определение 5.Вероятность события А, вычисленная при условии, что имело место другое событие В, называется условной вероятностью события А и обозначается 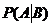 .
.
В примере 3): Р(А) = 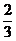 ,
, 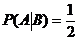 .
.
Условие независимости события А от события В: 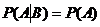 .
.
Условие зависимости события А от события В: 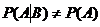 .
.
Теорема 3.Вероятность произведения двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое имело место.
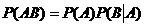
Доказательство.
Докажем для схемы урн истинность тождества формулы.
Пусть всевозможные исходы опыта сводятся к n случаям, которые изобразим в виде точек:
 Пусть событию А благоприятствует m случаев, событию В – k случаев, а т.к. события А и В совместны (мы не предполагали их несовместность), то событиям А и В одновременно благоприятствует l случаев.
Пусть событию А благоприятствует m случаев, событию В – k случаев, а т.к. события А и В совместны (мы не предполагали их несовместность), то событиям А и В одновременно благоприятствует l случаев.
Тогда, вероятности данных событий равны: 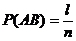 ,
, 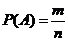 .
.
Вычислим условную вероятность 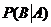 , т.е. условную вероятность события В в предположении, что А имело место. Если известно, что А произошло, то из ранее возможных n случаев остаются возможными только те, которые благоприятствовали событию А. Из них l случаев благоприятны событию В, следовательно,
, т.е. условную вероятность события В в предположении, что А имело место. Если известно, что А произошло, то из ранее возможных n случаев остаются возможными только те, которые благоприятствовали событию А. Из них l случаев благоприятны событию В, следовательно, 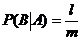 , т.е.
, т.е.
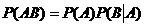 – истинно, т.к.
– истинно, т.к. 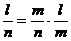 – истинное тождество. (что и треб. доказать).
– истинное тождество. (что и треб. доказать).
Замечание 1.При применении теоремы вполне безразлично, какое из событий А или В считать первым, а какое вторым, т.е. теорему можно записать в виде:
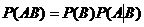
Замечание 2.В общем случае при Р(А) > 0, Р(В) > 0 условная вероятность выражается формулой: 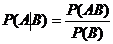 ,
, 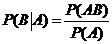 .
.
Следствие 1. Если событие А не зависит от события В, то и событие В не зависит от события А.
Замечание 3.Зависимость и независимость событий всегда взаимны.
Замечание 4.Условные вероятности обладают всеми свойствами, присущими обычным вероятностям:
1. 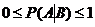 ,
,
2. если наступление события В исключает возможность осуществления А, т.е. 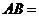 Ø, то
Ø, то
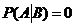 , если событие В ведет к обязательному осуществлению А, т.е.
, если событие В ведет к обязательному осуществлению А, т.е. 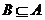 , то
, то 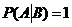 .
.
3. Если Ak – несовместные события, т.е. А = А1 + А2 +…+Аn, то 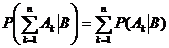 .
.
4. 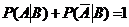 .
.
Замечание 5.Если А и В независимы, то независимы также события А и 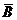 ,
, 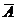 и В,
и В, 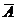 и
и 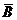 .
.
Теорема3/. ( Обобщенная теорема умножения зависимых событий).
Вероятность произведения нескольких зависимых событий равна произведению вероятностей этих событий, причем вероятность каждого следующего по порядку события вычисляется при условии, что все предыдущие имели место:
Р(А1 ∙ А2∙ А3 ∙….∙Аn) = Р(А1)∙ 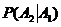 ∙
∙ 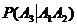 ∙…∙
∙…∙ 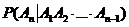 .
.
Теорема 4. (теорема умножения независимых событий).
Вероятность произведения двух независимых событий равна произведению вероятностей этих событий: 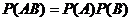 . (
. (
Теорема 4/. ( Обобщенная теорема умножения независимых событий).
Вероятность произведения нескольких независимых событий равна произведению вероятностей этих событий:
Р(А1 ∙ А2∙ А3 ∙….∙Аn) = Р(А1)∙ 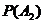 ∙
∙ 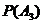 ∙…∙
∙…∙ 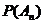 .
.
Примеры.
1. Из колоды карт последовательно вынуты две карты. Найти: а) вероятность того, что вторая карта окажется тузом (неизвестно, какая карта была вынута вначале), б) вероятность того, что вторая карта будет тузом, если первоначально тоже был вынут туз.
Решение.
Обозначим А = {появление туза вторым}, В = {появление туза первым}.
а) 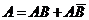 , где
, где 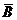 = {появление первым не туза}.
= {появление первым не туза}.
События 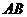 и
и 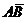 – несовместны, тогда по теореме 1 следует, что
– несовместны, тогда по теореме 1 следует, что
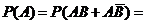
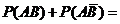 (события А и В, А и
(события А и В, А и 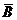 – зависимые, применим теорему 3) =
– зависимые, применим теорему 3) = 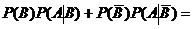
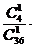
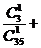
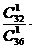
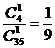 .
.
б) Если вынутая первая карта – туз , то в колоде осталось 35 карт и среди них только три туза, следовательно, 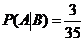 .
.
Или можно было найти эту вероятность, используя формулу условной вероятности:
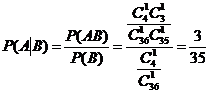 .
.
2.В урне 2 белых и 3 черных шара. Из урны вынимают подряд 2 шара. Найти вероятность того, что а) оба белые, б) оба белые, если после первого вынимания шар возвращают обратно в урну, и шары перемешиваются.
Решение.
Обозначим: А = {появление двух белых шаров}, В = {появление белого шара при первом вынимании}, С = {появление белого шара при втором вынимании}.
а) А = В∙С. События В и С – зависимы, тогда по теореме 3 следует, что
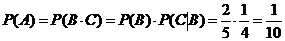 .
.
б) А = В∙С. События В и С – независимы, тогда по теореме 4 следует, что
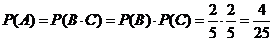 .
.
Теорема 5.Вероятность наступления события А, состоящего в появлении хотя бы одного из событий А1,А2, А3,…, Аn , независимых в совокупности, равна разности между 1 и произведением вероятностей противоположных событий:
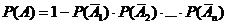 .
.
Если все 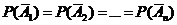 , то
, то 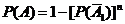 .
.
Пример.
Производится три выстрела по одной и той же мишени. Вероятности попадания при первом, втором и третьем выстрелах равны соответственно р1 = 0,4; р2 = 0,5; р3 = 0,7. Найти вероятность того, что в результате этих трех выстрелов в мишени будет хотя бы одна пробоина.
Решение.
Обозначим А = {хотя бы одно падание в цель}.
А1 = { падание в цель при первом выстреле}, А2 = { падание в цель при втором выстреле}, А3 = { падание в цель при третьем выстреле}.
Р(А1) = р1, Р(А2) = р2, Р(А3) = р3.
Можно расписать в алгебре событий данное событие в виде суммы произведений:
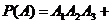
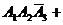
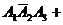
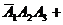
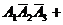
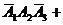
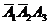 и найти вероятности слагаемых, где множители – независимые события. Но это нецелесообразно.
и найти вероятности слагаемых, где множители – независимые события. Но это нецелесообразно.
Перейдем от прямого события к противоположному: 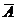 = { ни одного падания в цель}:
= { ни одного падания в цель}:
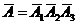 ,
,
где 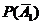 = 1– р1 =0,6,
= 1– р1 =0,6, 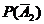 = 1 – р2 = 0,5,
= 1 – р2 = 0,5, 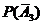 = 1 – р3 =0,3.
= 1 – р3 =0,3.
Тогда по теореме 5:
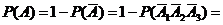 (т.к. события независимые, то по теореме 4) = =
(т.к. события независимые, то по теореме 4) = = 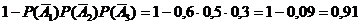 .
.
