Ковариация и коэффициент корреляции случайных величин. Связь между некоррелированностью и независимостью случайных величин.

Для кол-енного описания связи между двум.с.в.,вводят ковариацию и коэф.корреляции.

Опр. Ковариация Kxy с.в.X и Y;наз-ся м.о.произведения отклонения этих с.в.от своих м.о.

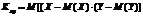
Т.ф-ля д/выч.ковариации

Ковариация XY равна м.о.их произведения минус произ.их м.о.

Kxy=M(XY)- M(X)M(Y)

Док. Пусть M((X)=a M(Y)=b тогда

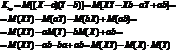
Следствие.сли X Y назависимы, то их ковариация равна нулю

К недостаткам ковариации относят то,что это размерная величина и поэтому харак-ет не только степень связи между компонентами, но и разброс значений компонентов. Поэтому вводят коэф.кор.

Опр.Коэф.кор.двух.с.в.(X,Y) наз-ся отношение их ковариации к произведению средних квадратических отклонений этих с.в.

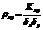
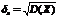
Св-ва:1. [-1,1] -1≤ρxy≤1

2. Если X Y независ. То ρxy=0

3. Если 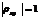, то между вел.X Y сущ.функциональная зависимость

При ρ=1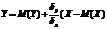

При ρ=1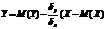

Для того что бы найти коэф.кор.по табл.распр.двум.с.в.надо:

1.

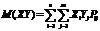
2. найти одномер.распр.X Y

3. по одномер распр найти: M(X),M(Y),D(X),D(Y)

4.Найти коэф.кор.по ф-ле:

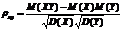
Заменяя в последнем выражении входящие величины на их выборочные оценки, получаем формулу для вычисления выборочного коэфф-нта корреляции r:

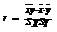
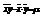
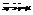-выбо-

рочная ковариация, т.к. , ; ;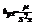

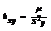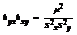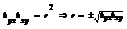, «+»,если 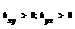; «-» если

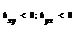.Если r>0,то связь между переменной называется прямой.Если r<0- связь называется обратной. Связь между переменными признается тесной, если |r|³0,7; умеренной если 0,4£|r|£0,7; слабой если |r|<0,4. Основное св-во коэфф-та корреляции: |r|£1.; Предельное значение коэфф-та корреляции: 1) |r|=1,т.и т.т.к. byx*bxy=1 => прямые регрессии совпадают. 2) r=0 т.и т.т.к. µ=0 ó byx=0 и bxy=0 => прямые регрессии перпендикулярны.; Если r=0 то говорят, что между переменными х и у отсутствует линейная корреляционная зависимость.

28. Неравенство Маркова (лемма Чебышева) (с выводом). Пример.

Пусть с.в.Х принимает только неотриц.знач.и имеет м.о.. Тогда для любого положит.А, верно неравенство:

А›0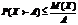

След.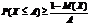

Неравенство Чебышева (с выводом) и его частные случаи для случайной величины, распределенной по биномиальному закону, и для частости события.

Т. Для любойс.в.,имеющей м.о.и дисперсию, справедливо нер.Чебышево:

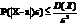где a=M(X),ε›0

Док. Обознач. a=M(X), рассмотрим Y=(X-a)²

Она прин.только не отриц. знач. M(Y)=M(X-a)²=D(X),т.е. у неё есть м.о.,след.к Y можно прим.нер-во Маркова

P(Y>)≤M(Y)/A

Возьмём A=ε², P(Y>ε²)≤D(X)/ε²

Y>ε²след. (X-a)²>ε²

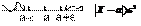
Т.о. (А) примет вид

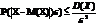
1.с.в.Х-бинум.зак.

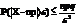
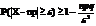
2.Пусть W-частота соб.в n незав.повтор.исп.

W=X_n/n X_n-сколько раз произош.соб

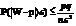
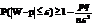
3.Пусть X1..Xn-незав.с.в., M(X)=a_i D(X)≤C

Тогда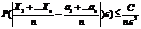

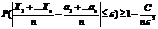
Неравенство Чебышева для средней арифметической случайных величин (с выводом).

Т.Бенулли Частость события в n независимых испытаниях, в каждом из которых оно может произойти с одной и тойже вер-ю p,при неограниченном увеличении числа n сходится к вер-ти p этого соб-я в отдельном исп-и

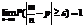
Или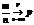

Вытекает из нер-ва Чебышева для частости собятия:

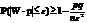
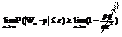
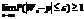
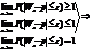
Теорема Чебышева (с доказательством), ее значение и следствие. Пример.

Пусть с.в.Х1..Хn имеют одинаковое м.о. а и дисперсия ограниченна одной и той же постоянной С,тогда верно:

M(Xi)=a D(Xi)≤C тогда

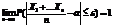
Вытекает из нер-ва Чебышева для частости собятия:

Смысл: При большом числе Х с.в. Х1…Хn практически достоверно, что их сред.ариф., которая явл.с.в.сколь мало отличается от конкретного числа a, т.е.практически перестаёт быть с.в..

Т.Чеб.принято наз.законом больших чисел. –это общ. принцип согласно кот.действия большого числа случ.факторов при весьма общих условиях приводит к результату почти независищяму от случая.

Закон больших чисел. Теорема Бернулли (с доказательством) и ее значение. Пример.

Т.Бенулли Частость события в n независимых испытаниях, в каждом из которых оно может произойти с одной и тойже вер-ю p,при неограниченном увеличении числа n сходится к вер-ти p этого соб-я в отдельном исп-и

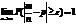
Или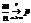

Вытекает из нер-ва Чебышева для частости собятия:

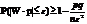
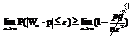
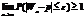
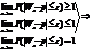
Смысл: При большом числе n практически достоверно, что частость собятия m/n величина случайная ,как угодно мало отличается от неслуч.вел. p-вер-ти соб-я,т.е.практически перестаёт быть слууч.

Т..принято наз.законом больших чисел. –это общ. принцип согласно кот.действия большого числа случ.факторов при весьма общих условиях приводит к результату почти независищяму от случая.