Функция распределения двумерной случайной величины

Функцией распределения двумерной случайной величины (X, Y), называется функция F(x, y), определяющая вероятность того, что компонента X примет значение, меньшее чем x, а компонента Y – меньшее, чем y.

F(x, y)=P(X <x, Y<y)

В одномерном случае функция распределения

F(x)=P(X <x)

равна вероятности того, что точка, соответствующая значению случайной величины X окажется правее x. В двумерном случае функция распределения равна вероятности того, что значение величины (X, Y) попадет в бесконечный квадрант расположенный левее и ниже точки (x, y), являющейся его вершиной (рис.10).

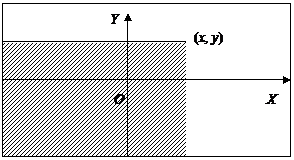
Рис. 10. Область X <x, Y<y

Когда «двумерная» функция распределения строится для дискретной случайной величины, вместо отрезков с постоянным значением функции распределения (как в одномерном случае) появляются участки плоскостей, образующие “ступенчатую” поверхность (каждая плоскость параллельна плоскости XOY)

Рассмотрим упрощенный случай, когда случайная величина распределена в соответствии с законом

	x1=0	x2=10
y1=10	p1	p2

Легко можно проверить, что значения функции для различных областей плоскости XOY будут такими, как показано на рис.11.

При x£0, y£10 F(x, y)=P(X <x, Y<y)=0

При x£0, y>10 F(x, y)=P(X <x, Y<y)=0

Если 0<x£10, y£10 F(x, y)=P(X <x, Y<y)=0

и при 0<x£10, y>10 F(x, y)=P(X <x, Y<y)= p₁

Наконец, при x>10, y£10 F(x, y)=P(X <x, Y<y)=0

и при x>10, y>10 F(x, y)=P(X <x, Y<y)= p₁+ p₂=1

Наша двумерная случайная величина принимает всего два значения (0, 10) и (10, 10), и для тех точек плоскости XOY, для которых квадрант с вершиной (x, y) не захватывает ни одного значения случайной величины, функция распределения равна 0. В области, где захватывается только точка (0, 10) функция распределения равна вероятности p₁, в области, где квадрант с вершиной (x, y) захватывает обе точки – единице.

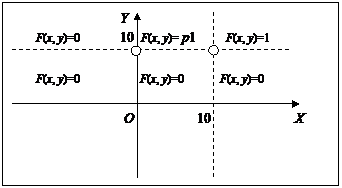
Рис. 11. Пример функции распределения для дискретной двумерной величины

Как и в одномерном случае, с помощью функции распределения можно задавать закон распределения непрерывной двумерной случайной величины. Для непрерывной двумерной случайной величины поверхность, отвечающая функции распределения, будет иметь более сложную форму. Рассмотрим в качестве примера функцию

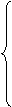0, x<0 или y<0

x×y/100, 0< x£10 и 0< y£10,

F(x, y)= y/10, 0< y£10 и x>10

x/10, 0< x£10 и y>10

1, или y>10

Области, на которых функция распределения принимает различные значения, показаны на рис.12

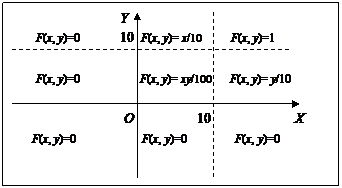Рис.12. Области различных значений функции распределения непрерывной двумерной случайной величины.

Пусть необходимо найти вероятность попадания случайной величины (X, Y) в квадрант (5, 6). В соответствии с приведенным выше законом распределения

P(X <5, Y<6)=5×6/100=0.3

Вероятность попадания в квадрант (5, 11)

P(X <5, Y<11)=5/10=0.5