Центральная предельная теорема в форме Ляпунова
Пусть у случайных величин в схеме серий существует математическое ожидание 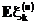 , дисперсия
, дисперсия 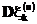 и третий абсолютный момент
и третий абсолютный момент  .
.
Предположим, без ограничения общности, что
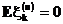
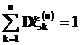
Пусть
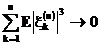
Тогда
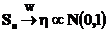
Доказательство.
Для доказательства используем следующие две леммы.
Лемма 1.
Если 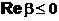 , то
, то
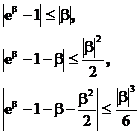
Доказательство леммы 1.
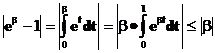
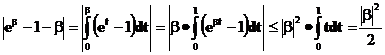
Третье неравенство доказывается аналогично.
Доказательство леммы 1 завершено.
Лемма 2.
Если 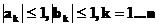 , то
, то
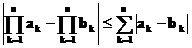
Доказательство леммы 2.
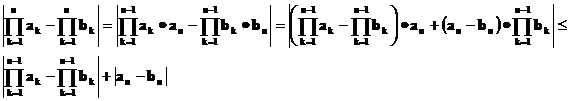 Доказательство леммы 2 завершено.
Доказательство леммы 2 завершено.
Доказательство теоремы.
Используя леммы 1 и 2 и равенство
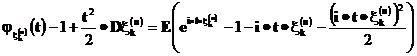
получаем
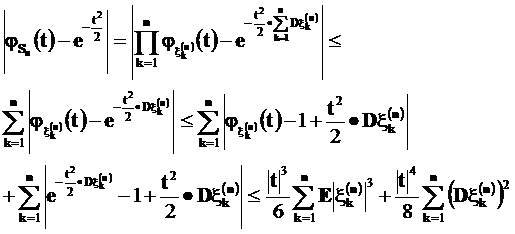 Первая сумма стремится к нулю по условиям теоремы, а вторая потому, что
Первая сумма стремится к нулю по условиям теоремы, а вторая потому, что
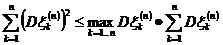
и по неравенству Ляпунова для моментов и условиям теоремы
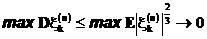
Теорема доказана.
Условное математическое ожидание, условная вероятность и условное распределение
Условное математическое ожидание является одним из основных понятий современной теории вероятностей. Оно позволяет дать корректное определение условной вероятности относительно возможных (непустых) событий, имеющих нулевую вероятность. Необходимость такого определения становится ясной из следующего примера.
Пусть 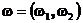 - случайная равномерно распределенная точка на единичном квадрате. Тогда случайные величины
- случайная равномерно распределенная точка на единичном квадрате. Тогда случайные величины 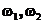 независимы, равномерно распределены на единичном отрезке и
независимы, равномерно распределены на единичном отрезке и
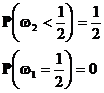
С одной стороны в силу независимости случайных величин 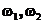 условная вероятность события
условная вероятность события 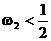 при условии
при условии 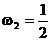 должна совпадать с его безусловной вероятностью
должна совпадать с его безусловной вероятностью
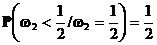
с другой стороны формальное вычисление этой условной вероятности по формуле условной вероятности
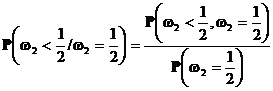
невозможно. Понятие условного математического ожидания позволяет дать новые, более общие, определения для условной вероятности и условного распределения.
Определение и основные свойства условного математического ожидания
Формальное определение условного математического ожидания является очень простым.
Пусть 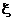 - случайная величина с конечным математическим ожиданием, заданная на
- случайная величина с конечным математическим ожиданием, заданная на
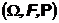
и 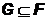 - некоторая сигма-алгебра.
- некоторая сигма-алгебра.
Случайная величина 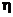 называется условным математическим ожиданием случайной величины
называется условным математическим ожиданием случайной величины 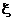 относительно
относительно 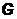 , если
, если
1. Случайная величина 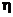
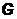 - измерима
- измерима
2. Для любого события 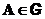
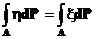
·
Условное математическое ожидание обозначается так
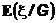
Напомним, что измеримость 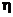 относительно
относительно 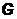 означает, что
означает, что
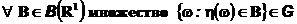
Заметим, что условие 2) в определении условного математического ожидания можно рассматривать как систему уравнений (количество уравнений равно количеству множеств в 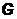 , при заданной
, при заданной 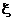 правая часть к важдом уравнении известна) на функцию
правая часть к важдом уравнении известна) на функцию 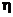 , а условие 1) как описание класса функций, в котором ищется решение уравнения 2).
, а условие 1) как описание класса функций, в котором ищется решение уравнения 2).
Прежде, чем исследовать вопросы существования и единственности условного математического ожидания в общей ситуации, приведем примеры вычисления условных математических ожиданий исходя из этого определения.
ПРИМЕР 1.
Пусть 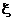 - случайная величина с конечным математическим ожиданием, заданная на
- случайная величина с конечным математическим ожиданием, заданная на
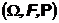
и 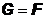
Тогда класс функций, в котором ищется решение уравнения 2), совпадает с классом всех случайных величин заданных на
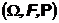
и, следовательно, можно положить 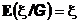
Таким образом, сама случайная величина 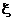 является частным случаем условного математического ожидания, если положить
является частным случаем условного математического ожидания, если положить 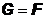
ПРИМЕР 2.
Пусть 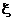 - случайная величина с конечным математическим ожиданием, заданная на
- случайная величина с конечным математическим ожиданием, заданная на
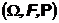
и 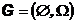
Тогда класс функций, в котором ищется решение уравнения 2), совпадает с классом измеримых относительно тривиальной сигма-алгебры функции т.е. всех констант и уравнений всего 2
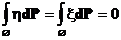 ,
,
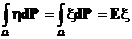 ,
,
следовательно, можно положить 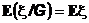
Таким образом, математическое ожидание является частным случаем условного математического ожидания, если положить 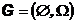
ПРИМЕР 3.
Пусть 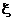 - случайная величина с конечным математическим ожиданием, заданная на
- случайная величина с конечным математическим ожиданием, заданная на
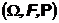
и сигма-алгебра 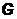 порождена некоторым событием A
порождена некоторым событием A 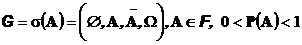
Тогда класс функций, в котором ищется решение уравнения 2), совпадает с классом простых функций , принимающих два значения, соответственно, на множествах 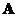 и
и 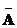 . Обозначим их , например,
. Обозначим их , например, 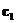 и
и 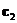
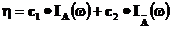
Уравнений всего 4
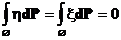 ,
,
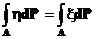
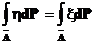
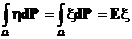 ,
,
причем первое из них не накладывает никаких ограничений на функцию 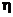 , а четвертое следует из второго и третьего.
, а четвертое следует из второго и третьего.
Так как случайная величина 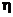 постоянна на множествах
постоянна на множествах 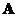 и
и 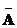 то, из второго и третьего уравнений можно определить значения
то, из второго и третьего уравнений можно определить значения 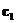 и
и 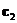
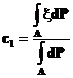
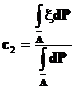
Нетрудно обобщить этот пример на случай сигма-алгебры , порожденной некоторым конечным разбиением пространства элементарных исходов.
ПРИМЕР 4.
Пусть 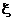 - случайно выбранная на единичном отрезке точка
- случайно выбранная на единичном отрезке точка
| Покажите, что набор всех симметричных относительно ½ борелевских подмножеств единичного отрезка является сигма-алгеброй. Множество симметрично относительно ½, если вместе с точкой х оно содержит точку 1-х. | и сигма-алгебра 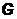 является сигма-алгеброй всех симметричных относительно точки ½ борелевских множеств единичного отрезка. Тогда класс функций, в котором ищется решение уравнения 2), совпадает с классом функций , графики которых симметричны относительно прямой х=1/2 . Выбирая, в качестве множества A, симметричное при х<1/2 множество является сигма-алгеброй всех симметричных относительно точки ½ борелевских множеств единичного отрезка. Тогда класс функций, в котором ищется решение уравнения 2), совпадает с классом функций , графики которых симметричны относительно прямой х=1/2 . Выбирая, в качестве множества A, симметричное при х<1/2 множество 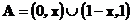 получим получим |
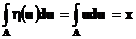
Так как график 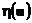 симметричен относительно центра единичного отрезка, получаем
симметричен относительно центра единичного отрезка, получаем
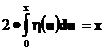
откуда следует, что