Нормальное (гауссовское) распределение.

Рассмотрим положительную функцию

Докажите это, переходя к полярным координатам в интеграле , который , очевидно, равен квадрату исходного.

Так как то функция

является плотностью и задает так называемое стандартное нормальное (гауссовское) распределение.

График этой плотности приведен на рисунке

Общее нормальное распределение задается плотностью

где

параметры распределения.

Покажите, что если ,то

Нормальное распределение обладает большим количеством замечательных свойств, многие из которых мы рассмотрим в дальнейшем. Это распределение использовал Гаусс Карл Фридрих в модели случайных ошибок измерения. Случайная величина, имеющая нормальное распределение, называется нормальная или гауссовская случайная величина. Для этого распределения используют обозначение

.

Графики плотности

Экспоненциальное (показательное) распределение.

Рассмотрим плотность

где

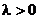
параметр распределения. Распределение с такой плотностью называется экспоненциальное или показательное распределение. Приведем график плотности этого распределения при

Для доказательства достаточно воспользоваться формулой условной вероятности. Можно показать, что экспоненциальное распределение это единственное распределение, из распределений имеющих плотность, с таким свойством.

Экспоненциальное распределение применяется при моделировании различных временных интервалов - времени жизни технических устройств, интервалов между моментами регистрации радиоактивных частиц датчиками радиации, интервалов между последовательными звонками в телефонной сети и т.п. Это распределение обладает замечательным свойством, которое называется отсутствие последействия. Именно, если имеет экспоненциальное распределение, то

Покажите, что, если 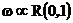,то

С точки зрения теории надежности это распределение описывает нестареющий элемент, т.е. в любой момент времени элемент имеет то же распределение остаточного времени жизни, что и новый элемент. Случайная величина, имеющая такое распределение называется экспоненциальная или показательная случайная величина. Это распределение обозначается

Гамма-распределение.

Рассмотрим плотность

где

параметры распределения. Распределение с такой плотностью называется гамма распределение. Приведем график плотности этого распределения при

Величина

рассматриваемая как функция переменной

называется гамма-функцией и имеет следующие, легко доказываемые свойства

Это распределение обозначается

Гамма распределение обобщает экспоненциальное распределение и превращается в него при

Гамма распределение с целым параметром

называется распределение Эрланга порядка и обозначается

Распределение

где n – целое, называется распределение хи-квадрат и обозначается