Множество рациональных чисел
Множество рациональных чисел – Qпринадлежит борелевской сигма-алгебре как объединение счетного числа одноточечных множеств.
Множество иррациональных чисел
Принадлежит борелевской сигма-алгебре как дополнение множества рациональных чисел.
Множество положительности непрерывной функции
Пусть
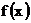
непрерывная функция. Тогда множество
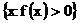
является борелевским.
Действительно, для любой точки x, в которой непрерывная функция положительна, найдется интервал, окружающий точку x, в котором эта функция также положительна. Для доказательства достаточно представить множество
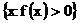
в виде объединения всех таких интервалов с рациональными центрами.
Другие множества
Пусть
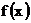
непрерывная функция.
Тогда множества
, 
, 
,….
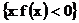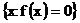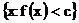являются борелевскими.
Неборелевские множества
Таким образом, можно привести массу примеров практически важных борелевских множеств. Возникает вопрос: может быть все множества на прямой борелевские?
Обозначим
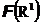
наибольшую сигма-алгебру, т.е. сигма-алгебру, включающую в себя все подмножества действительных чисел
Тогда, очевидно, что
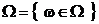
Но, оказывается, что
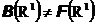
Доказательство этого утверждения (пример неборелевского множества на действительной прямой) содержится в курсе функционального анализа.
Варианты определения борелевской сигма-алгебры
Борелевская сигма-алгебра определена как минимальная сигма-алгебра, содержащая все интервалы вида
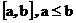
т.е.
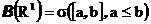
Ясно, теперь, что
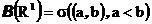
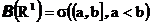
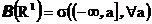
и т.д.
Определение случайной величины
Пусть
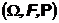
основное вероятностное пространство
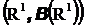
действительная прямая с борелевской сигма-алгеброй
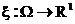
поточечное измеримое отображение, ставящее в соответствие каждому элементарному исходу основного пространства действительное число. Это отображение называется случайная величина.
Вероятностная мера, определенная на борелевской сигма-алгебре по формуле
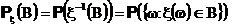
называется распределением случайной величины.
Необходимые и достаточные условия измеримости
Пусть D – некоторый набор подмножеств действительной прямой, такой что
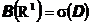
Для того, чтобы отображение
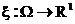
было случайной величиной, необходимо и достаточно, чтобы для любого множества
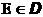
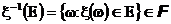
Доказательство.
Необходимость очевидна.
Множества E такие, что
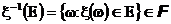
образуют сигма-алгебру, которая содержит в себе D. Следовательно, она совпадает с борелевской.
Доказательство закончено.
Борелевская функция
| Заметим, что в определении случайной величины не участвует вероятность. Поэтому в этом определении не требуется указывать, какая вероятность действует на основном пространстве. | Случайная величина, заданная на основном пространстве, которое является действительной прямой с борелевской сигма-алгеброй, называется борелевская функция.  |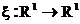
Примеры борелевских функций
Любая непрерывная функция является борелевской, т.к. любое множество вида
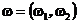
является борелевским
и
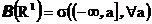
Функции
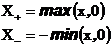
поэтому тоже являются борелевскими.
Если f и g – две борелевские функции, то
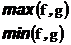
тоже борелевские, т.к.
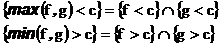
Аналогично, если
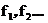- последовательность борелевских функций, то
и
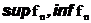
-борелевские функции (может быть принимающие значения
)
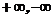Заметим, что множество значений x, для которых существует предел последовательности 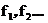также явялется борелевским.
Примеры случайных величин
Индикатор события
Пусть A – случайное событие. Тогда функция
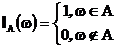
является случайной величиной и называется индикатор события A
Верно и обратное – любая случайная величина принимающая значения 0 или 1 является индикатором некоторого события A.
Часто, для краткости, будем пользоваться обозначением
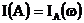
Простая случайная величина
Пусть
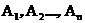
полная группа событий.
Случайная величина
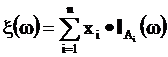
называется простая случайная величина.
Верно и обратное – любая случайная величина принимающая конечное число значений
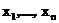
является простой .