Расчет неразрезной (статически неопределимой) балки

Расчет неразрезной (статически неопределимой) балки с помощью уравнений трех моментов и метода фокусных отношений.

Уравнение трех моментов

1) Ставятся шарниры над всеми промежуточными опорами.

2) Если одна из опор является жесткой заделкой, то вместо нее добавляется пролетL=0:

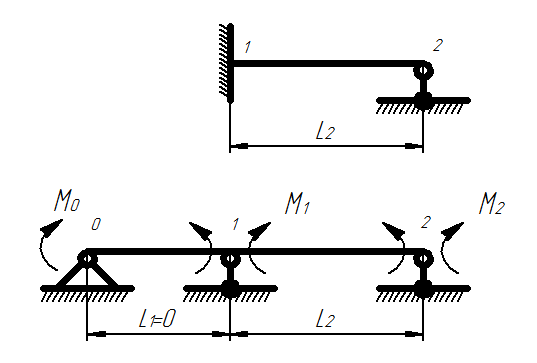
Неразрезная балка

3) Консольные части балки удаляются, а их влияние заменяется изгибающими моментами:

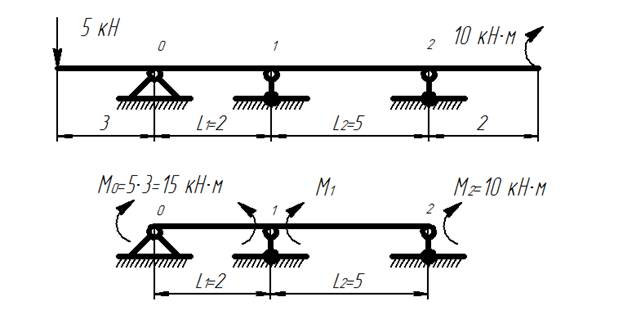
Неразрезная балка

4) Нумеруются пролеты (пролет нумеруется последующей за ней опорой) и опоры (начиная с 1).

5) Строятся эпюры изгибающих моментов для отдельных балок, на которые действуют внешние нагрузки.

6) Составляются уравнения трех моментов:

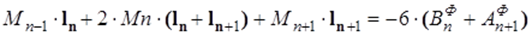
где М_n-1, M_n, M_n+1 – моменты в опорах n-1, n, n+1.

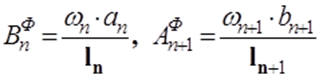
где ω_n, ω_n+1 – площади фигур, ораниченных эпюрами изгибающих моментов для отдельных (простых) балок;

a_n, b_n+1 – расстояние от центра тяжести соответствующей эпюры изгибающих моментов простой балки до левой опоры n и правой опоры n+1.

7) Определяются площади и центры тяжести соответствующих эпюр изгибающих моментов простых балок.

Для прямоугольного треугольника:

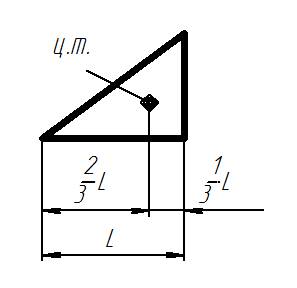
Центр тяжести для треугольника

7) Решаются уравнения трех моментов:

8) Строится эпюра моментов в опорах М_оп.

9) Строится итоговая эпюра моментов М, равная сумме эпюр моментов в опорах М_опи всех эпюр M_р, построенных для отдельных балок.

10) Проверка – произведение единичной эпюры от действия единичной силы в крайней правой опоре на итоговую эпюру должно равняться нулю.

Метод фокусных отношений

1) Если есть заделка, то по аналогии с уравнением трех моментов вместо заделки добавляется пролет L=0.

2) Определяются фокусные расстояния (левые и правые).

Левые фокусные отношения определяются по формуле:

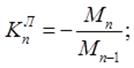
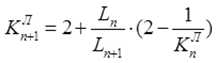
Правые фокусные отношения определяются по формуле:

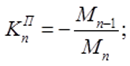
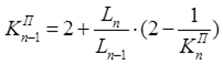
При шарнирномопирании крайнего левого (правого) пролета фокусное расстояние для следующего номера опоры (крайней опоры) равно бесконечности (∞).3) Строятся эпюры изгибающих моментов для балки от действия заданной временной нагрузки.

Моменты в опорах определяются по формулам:

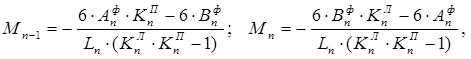
где A_n^ф, В_n^ф – левая и правая фиктивные опоры соответственно (n – номер пролета) – определяются как в способе трех моментов.

Моменты в остальных пролетах определяются по формулам:

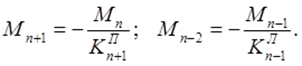
4) Строится объемлющаю эпюра. Она строится при одновременном действии временной нагрузки во всех пролетах и постоянной нагрузки.

Максимальные значения определяем сложением значений из эпюры изгибающего момента от действия постоянной нагрузки с положительными значениями эпюр изгибающего момента от действия временной нагрузки в рассматриваемых точках.

Минимальные значения определяем сложением значений из эпюры изгибающего момента от действия постоянной нагрузки с отрицательными значениями эпюр изгибающего момента от действия временной нагрузки в рассматриваемых точках.

С. Задача 1

Построить эпюру изгибающих моментов для неразрезной балки с помощью уравнения трех моментов.

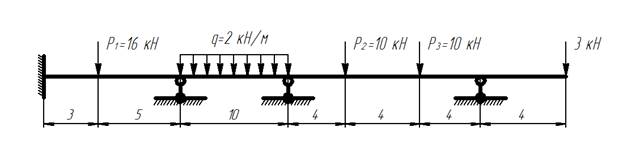
Неразрезная балка

1) Составляется основная система неразрезной балки:

Основная система для способа уравнений трех моментов

2) Строятся эпюры изгибающих моментов для отдельных балок, на которые действуют внешние нагрузки:

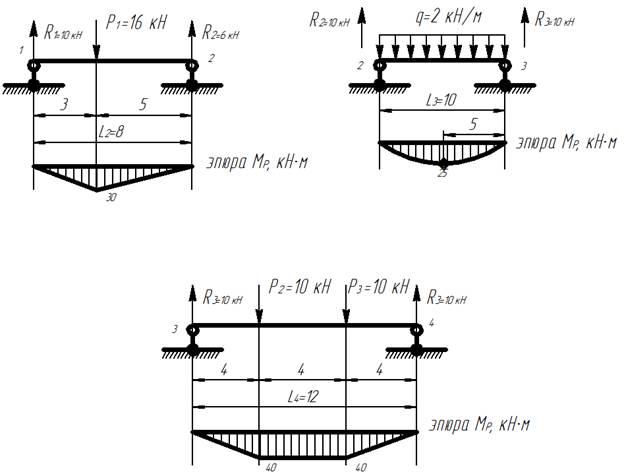
Эпюры изгибающих моментов для отдельных балок

Распишем построение эпюры для пролета L₂:

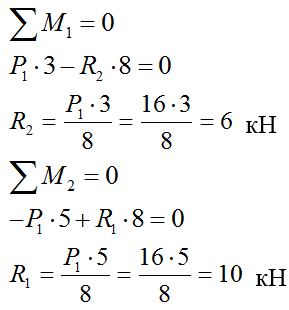
и т.д. для остальных пролетов.

3) Составляются уравнения трех моментов:

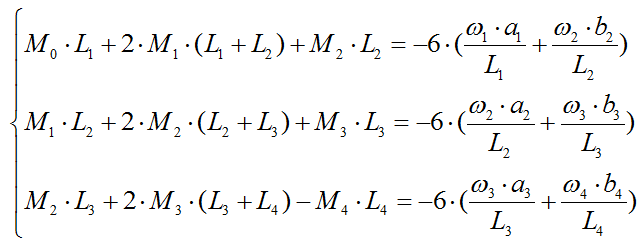
4) Определяются площади и центры тяжести соответствующих эпюр изгибающих моментов простых балок:

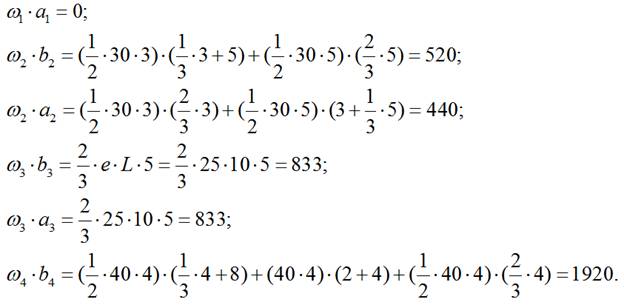
5) Преобразуем уравнения трех моментов:

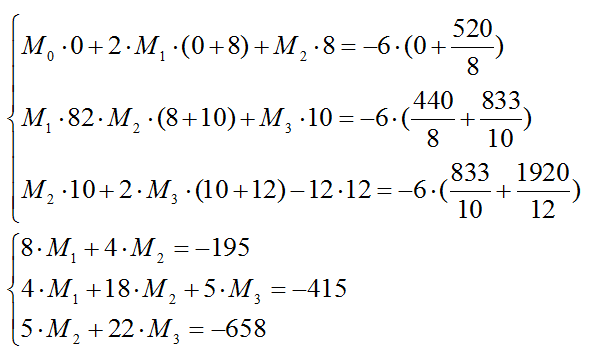
6) Решаем уравнения трех моментов:

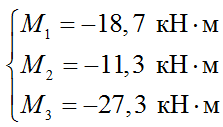
7) Строим эпюру моментов в опорах М_оп.

8) Строим итоговую эпюру моментов М, равную сумме эпюр моментов в опорах М_опи всех эпюр M_р, построенных для отдельных балок.

9) Выполняем проверку. Строим единичную эпюру от действия единичной силы в крайней правой опоре. Если произведение единичной эпюры на итоговую эпюру равно нулю, то расчет выполнен верно.

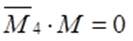
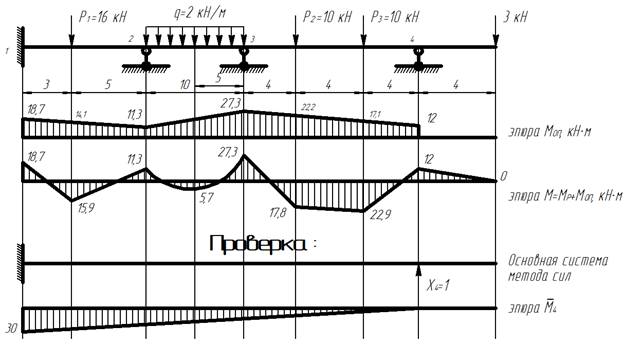
Расчет неразрезной балки с помощью уравнений трех моментов

С. Задача 2

Построим для заданной балки эпюры изгибающих моментов способом фокусных отношений в результате последовательного загружения всех пролетов временной нагрузкой (например, q_вр=1,5 кН/м). Для пролета L₃ построим объемлющую эпюру для точек 2, 3, 0,5·L₃.

По аналогии с методом уравнений трех моментов, если есть заделка, то вместо нее добавляется пролет L=0 (на схеме балке не указан, т.к. схема аналогична задаче для метода трех моментов).

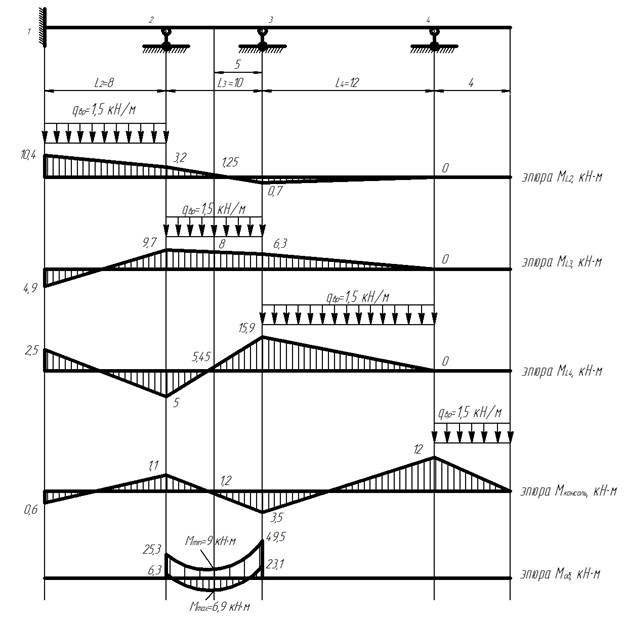
Расчет неразрезной балки способом фокусных отношений

1) Определяем фокусные расстояния (левые и правые):

1.1) левые:

При шарнирном опирании крайнего левого пролета фокусное расстояние для следующего номера опоры равно бесконечности (∞) в соответствии с формулой:

М_n-1 =0, т.к. крайняя опора n-1 является шарнирной, т.е.:

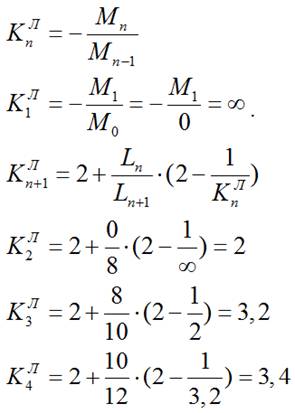
1.2) правые:

При шарнирном опирании крайнего правого пролета фокусное расстояние для номера крайней опоры равно бесконечности (∞) в соответствии с формулой:

М_n =0, т.к. крайняя опора n является шарнирной, т.е.:

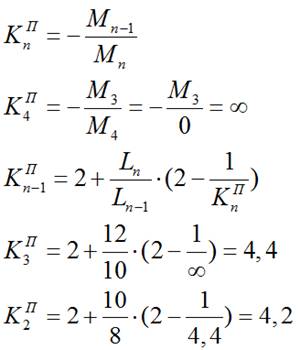
2) Строим эпюру изгибающих моментов для балки от действия временной нагрузкиq_вр в пролете L₂:

2.1) Определяем фиктивные опорные реакции от q_{вр (по формуле для способа уравнений трех моментов)}:

Для распределенной нагрузки может применяться следующая формула:

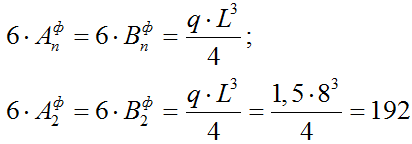
2.2) Определяем моменты в опорах:

Моменты в опорах определяются по формулам:

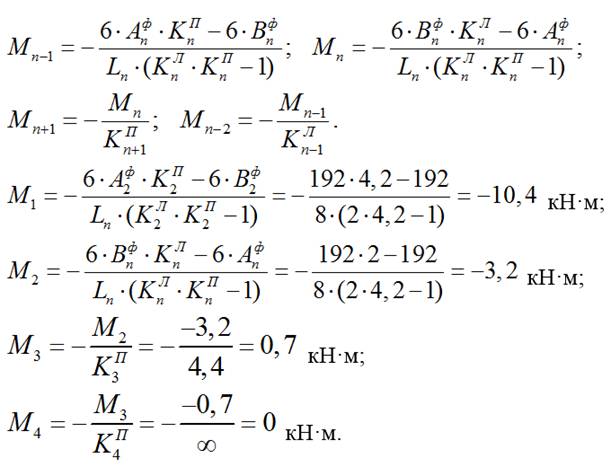
3) Строим эпюру изгибающих моментов для балки от действия временной нагрузкиq_вр в пролете L₃:

3.1) Определяем фиктивные опорные реакции от q_вр:

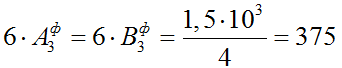
3.2) Определяем моменты в опорах:

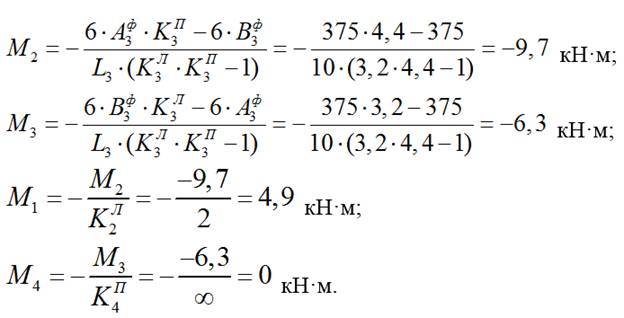
4) Строим эпюру изгибающих моментов для балки от действия временной нагрузкиq_вр в пролете L₄:

4.1) Определяем фиктивные опорные реакции от q_вр:

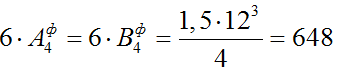
4.2) Определяем моменты в опорах:

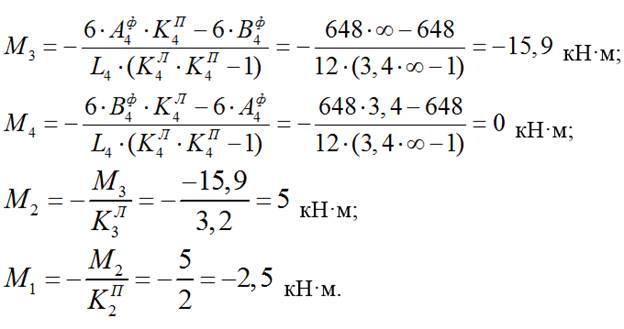
5) Строим эпюру изгибающих моментов для балки от действия временной нагрузкиq_вр, действующей на консоли:

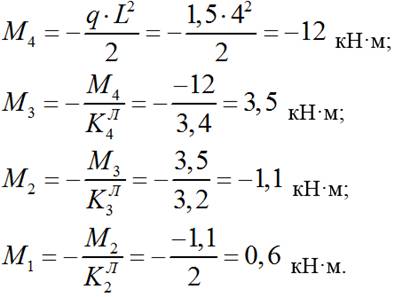
6) Строим объемлющую эпюру для пролета L₃ (точек 2, 3, 0,5·L₃). Она строится при одновременном действии временной нагрузки во всех пролетах и постоянной нагрузки.

Значения эпюры изгибающего момента от действия постоянной нагрузки берем из решения задачи 1 с помощью уравнения трех моментов.

Максимальные значения определяем сложением значений из эпюры изгибающего момента от действия постоянной нагрузки с положительными значениями эпюр изгибающего момента от действия временной нагрузки в рассматриваемых точках.

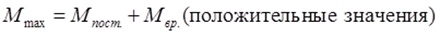
Минимальные значения определяем сложением значений из эпюры изгибающего момента от действия постоянной нагрузки с отрицательными значениями эпюр изгибающего момента от действия временной нагрузки в рассматриваемых точках.

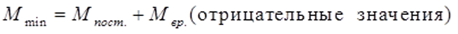
Полученные значения для удобства записи заносим в таблицу 1:

Таблица 1