Внутренние и внешние (опоры) связи

Внутренние и внешние (опоры) связи

Связи в расчетных схемах инженерных конструкций строительной механики, которые соединяют друг с другом отдельные ее части (стержни, пластины и т.д.) называютсявнутренними.

Виды внутренних связей:

- шарнирные (лишают двух степеней свободы) (рис. 1, а);

- шарнирно-подвижные (лишают одной степени свободы) (рис. 1, б).

Рисунок 1. Внутренние связи

Взаимодействие между рассматриваемым сооружением и другими инженерными конструкциями или фундаментом в расчетных схемах учитывается с помощью внешних связей – опор.

Виды внешних связей (опор):

- шарнирно-подвижная;

- шарнирно-неподвижная;

- жесткое защемление (заделка).

Расчет однопролетных балок

Задачи по определению внутренних усилий в однопролетных балках входят в курс предметов "Строительная механика" и "Сопротивление материалов".

Количество степеней свободы для плоской стержневой системы определяется по формуле, называемой основной формулой кинематического анализа:

W = 3Д – 2Ш – С₀

При W=0 –система неизменяема и статически определима (т.е. может быть решена путем составления уравнений равновесия).

Для определения реакций в опорах применяется принцип освобождения от связей – систему можно освободить от связей, если эти связи (например, опоры) заменить реакциями. Далее составив уравнения равновесия для новой полученной системы определяют величины введенных реакций.

Уравнения равновесия для плоской системы можно составить в следующих видах:

В элементах стержневой системы на плоскости могут возникать три вида внутренних усилий: продольная сила N, поперечная сила Q, изгибающий момент M. Положительные значения указанных усилий в зависимости от направления внутренних усилий определяются как на рис. 1:

Рисунок 1. Правило знаков для внутренних усилий

Методы определения усилий в статически определимых системах

Для определения усилий в строительной механике применяются различные методы: простых сечений, совместных сечений, вырезания узла и замены связей.

Метод простых сечений

При расчете этим метод внутреннее усилие рассматривают как внешнюю нагрузку и определяют его путем составления и решения уравнения равновесия.

Например, внутренние усилия балки (рис. 1, а).

Рисунок 1. Метод простых сечений

Алгоритм расчета данным методом:

1) провести через любую точку стержня разрез;

2) отбросить более сложную часть (где больше сил) и для дальнейшего расчета используют более простую часть стержня;

3) составить уравнения равновесия;

4) решая полученные уравнения, определить внутренние усилия M, Q, N;

5) построить эпюры M, Q, N по найденным значениям внутренних усилий.

Метод совместных сечений

Данный метод применяется при расчете составных систем.

Например, при расчете трехдисковой рамы (рис. 2, а) проводятся три совместных сечения I, II, III. В точках рассечения междисковых связей появляются 9 реакций (рис. 2, б): реакции в опорах R₁, R₂, H и реакции X₁, X₂, X₃,Y₁, Y₂, Y₃. Величины данных реакций определяются посредством составления уравнений равновесия.

Рисунок 2. Метод совметсных сечений

Алгоритм расчета данным методом:

1) провести через несколько точкек для рассматриваемой системы разрезы, деля данную конструкцию на составные части;

2) отметить возникшие реакции в рассеченных связях;

3) для каждой полученной составной части диска составить уравнения равновесия;

4) рассчитать систему полученных уравнений;

5) построить эпюры для каждой составной части заданной конструкции;

6) построить совместные эпюры для всей системы.

Метод вырезания узла

Данный метод применяется при расчете внутренних усилий в простых системах.

Алгоритм расчета данным методом:

1) можно вырезать узел только с двумя стержнями, сходящимися в нем, внутренние усилия в которых неизвестны;

2) продольные силы, действующие в узле, проецируются на соответствующие оси (для плоской системы x и y);

3) решая составленные уравнения, определяют неизвестные внутренние усилия.

Метод замены связей

Данный метод применяется при определении внутренних усилий в сложных статически определимых систем, для расчета которых использовать выше перечисленные способы трудно.

Алгоритм расчета данным методом:

1) сложная система преобразуется в более простую посредством перемещения связей;

2) из условия равенства изначально заданной и заменяющей систем определяется внутреннее усилие в переставленной связи;

3) полученная система рассчитывается одним из выше описанных способов.

Примеры задач с решениями.

С. Задача 1

Построить эпюры внутренних усилий для балки.

Подробнее: С. Задача 1

С. Задача 2

Построить эпюры внутренних усилий для балки.

Подробнее: С. Задача 2

С. Задача 3

Построить эпюры внутренних усилий для однопролетной ломаной балки.

Подробнее: С. Задача 3

С. Задача 4

Построить эпюры внутренних усилий для консольной ломаной балки.

Подробнее: С. Задача 4

Примеры с решениями.

С. Задача 1

Построить эпюры внутренних усилий для балки.

Однопролетная балка

1) Определяем реакции в опорах:

Т.к., значение реакции R_A получилось отрицательным, то меняем ее направление на расчетной схеме (новое направление обозначаем пунктирной линией), учитывая в дальнейшем новое направление и положительное значение этой реакции.

Проверка:

2) Строим эпюру изгибающих моментов М (построение эпюры ведется с любого "свободного" конца балки):

3) Строим эпюру поперечных сил Q. Производим построение эпюры поперечных сил (Q), используя формулу Журавского:

где М_пр, М_лев – ординаты изгибающего момента на правом и левом концах рассматриваемого участка балки;

l – длина рассматриваемого участка балки;

q – величина распределенной нагрузки на рассматриваемом участке.

Знак «±» в формуле ставится в соответствии с правилом знаков поперечных сил, рассмотренным выше (рисунок 1).

С. Задача 2

Построить эпюры внутренних усилий для составной рамы.

Разделяем составную раму на две части: вспомогательную и основную (статически определимую и геометрически неизменяемую).

Расчет начинаем со вспомогательной рамы.

Составная рама

Вспомогательная часть рамы

1) Определяем реакции в опорах:

Проверка:

2) Строим эпюру изгибающих моментов М:

3) Строим эпюру поперечных сил Q:

Эпюры внутренних усилий для вспомогательной рамы

4) Строим эпюру продольных сил N:

Рассматриваем узел G:

Вырезание узла дляпостроение эпюры продольных сил

Рассматриваем основную часть. Число степеней свободы для основной рамы должно равняться 0 (статически определимая и геометрически неизменяемая):

Переносим реакции в шарнире Ш₁ со вспомогательной части на основную, меняя направление.

Основная часть составной рамы

1.1) Определяем реакции в опорах:

Проверка:

1.2) Определяем реакции в опорах:

Проверка:

2) Строим эпюру изгибающих моментов М:

Определим значение изгибающего момента в шарнире Ш₂:

Т.к., значение изгибающего момента в шарнире должно равняться нулю.

3) Строим эпюру поперечных сил Q:

Эпюры внутренних усилий для основной части составной рамы

4) Строим эпюру продольных сил N:

Рассматриваем узел K:

Поскольку на балке BK в точке Ш₁ находится сила, действующая вдоль балки (т.е. продольная), то в этом месте должен быть скачок на ее величину на эпюре продольных сил (N). Методом вырезания узла K определено значение продольной силы на балке BK возле узла K. Поскольку усилие RШ₁ направлено к узлу, то скачок в точке Ш₁ будет в «−».

Рассматриваем узел N (на балке правее узла N не возникает продольной силы, т.к. на ней нет внешних нагрузок, действующих вдоль балки):

Вырезание узлов дляпостроение эпюры продольных сил

С. Задача 2

Построить эпюры внутренних усилий для балки.

Консольная балка

1) Определяем реакции в опорах:

2) Строим эпюру изгибающих моментов М:

3) Строим эпюру поперечных сил Q:

С. Задача 3

Построить эпюры внутренних усилий для однопролетной ломаной балки.

Ломаный стержень

1) Определяем реакции в опорах:

Проверка:

2) Строим эпюру изгибающих моментов М:

3) Строим эпюру поперечных сил Q:

4) Строим эпюру продольных сил N:

С. Задача 4

Построить эпюры внутренних усилий для консольной ломаной балки.

Ломаная балка

1) Определяем реакции в опорах:

2) Строим эпюру изгибающих моментов М:

3) Строим эпюру поперечных сил Q:

4) Строим эпюру продольных сил N:

Расчет многопролетных балок

Расчет статически определимой многопролетной балки при расчете сооруженийнеобходимо начинать с анализа взаимодействия отдельных ее элементов и построения «поэтажной схемы» многопролетной балки.

Поэтажные схемы для многопролетных балок

Проверку на геометрическую неизменяемость и статическую определимость для многопролетной балки выполняют по основной формуле кинематического анализа.

При построении поэтажной схемы в многопролетной балке выделяют основные и вспомогательные балки.

Виды основных балок:

Виды основных балок

Вспомогательную балку можно удалить из многопролетной балки без нарушения неизменяемости оставшейся части, поэтому вспомогательную балку можно рассчитать независимо от оставшейся части, причем ее опорные реакции будут служить внешними силами для оставшейся. Вспомогательные балки опираются на основные и поэтому при построении поэтажной схемы их располагают над основными, т.е. все вышерасположенные балки являются вспомогательными по отношению к нижерасположенным. Соответственно, расчет многопролетной балки начинают с самой верхней вспомогательной балки, представляя ее как статически определимую и геометрически неизменяемую систему.

С. Задача 1

Построить эпюры внутренних усилий для многопролетной балки.

Строим поэтажную схему для многопролетной балки.

Подробнее: С. Задача 1

С. Задача 2

Построить эпюры внутренних усилий для многопролетной балки.

Строим поэтажную схему для многопролетной балки.

Подробнее: С. Задача 2

С. Задача. Метод матриц

Построить эпюры внутренних усилий и линии влияния для указанного сеченияметодом матриц.

С. Задача 1

Построить эпюры внутренних усилий для многопролетной балки.

Строим поэтажную схему для многопролетной балки.

Многопролетная балка

Рассчитываем балку Ш₂С:

Балка Ш₂С

Определяем реакции в опорах:

Проверка:

Построение эпюр выполняется как для простой однопролетной балки.

Рассчитываем балку Ш₁Ш₂:

Балка Ш₁Ш₂

Определяем реакции в опорах:

Проверка:

Рассчитываем балку АШ₁:

Балка АШ₁

Определяем реакции в опорах:

С. Задача 2

Построить эпюры внутренних усилий для многопролетной балки.

Строим поэтажную схему для многопролетной балки.

Многопролетная балка

Рассчитываем балку АШ₁:

Балка АШ₁

Определяем реакции в опорах:

Проверка:

Рассчитываем балку Ш₂D:

Балка Ш₂D

Определяем реакции в опорах:

Проверка:

Рассчитываем балку BC:

Балка BC

Определяем реакции в опорах:

Проверка:

Примеры с решениями.

Линии влияния изгибающих моментов для шарнирно-опертых балок

Линии влияния поперечных сил для шарнирно-опертых балок

Линии влияния изгибающих моментов и поперечных сил для консольных балок

С. Задача 1

Построить линии влияния реакций и внутренних усилий для простой однопролетной балки.

Линии влияния для простой однопролетной балки

1) Определяем реакции в опорах. Силу Р=1 "привязываем" к одной из опор (введенная система координат имеет положительные значения в направлении x):

2) Рассматриваем случай расположения силы Р=1 справа от сечения k:

Рассматриваем характерные точки: x=0; 4; -5.

При этом рассматриваем действие сил, лежащих левее сечения k.

3) Рассматриваем случай расположения силы Р=1 слева от сечения k:

Рассматриваем характерные точки: x=4; 6; 9.

При этом рассматриваем действие сил, лежащих правее сечения k.

С. Задача 2

Построить линии влияния реакций и внутренних усилий для простой консольной балки.

Линии влияния для консольной балки

1) Определяем реакции в опорах:

2) Рассматриваем случай расположения силы Р=1 справа от сечения k:

Рассматриваем характерные точки: x=0; 4.

При этом рассматриваем действие сил, лежащих левее сечения k.

3) Рассматриваем случай расположения силы Р=1 слева от сечения k:

Рассматриваем характерные точки: x=4; 6.

При этом рассматриваем действие сил, лежащих правее сечения k.

С. Задача 3

Построить линии влияния внутренних усилий для простой однопролетной балки.

Линии влияния для простой однопролетной балки

1) Определяем реакции в опорах:

2) Рассматриваем случай расположения силы Р=1 справа от сечения k:

Рассматриваем характерные точки: x=0; -2.

При этом рассматриваем действие сил, лежащих левее сечения k.

3) Рассматриваем случай расположения силы Р=1 слева от сечения k:

Рассматриваем характерные точки: x=0; 4; 6.

При этом рассматриваем действие сил, лежащих правее сечения k.

С. Задача 4

Построить линии влияния внутренних усилий для простой однопролетной балки и рассчитать по ним усилия в сечении.

Линии влияния для простой однопролетной балки

1) Определяем реакции в опорах:

2) Рассматриваем случай расположения силы Р=1 справа от сечения k:

Рассматриваем характерные точки: x=0; 5; -2.

При этом рассматриваем действие сил, лежащих левее сечения k.

3) Рассматриваем случай расположения силы Р=1 слева от сечения k:

Рассматриваем характерные точки: x=5; 8.

При этом рассматриваем действие сил, лежащих правее сечения k.

4) Определяем усилие в сечении k:

- для изгибающего момента М_k:

- для поперечной силы Q_k:

Полученные значения соответствуют значениям на эпюрах в сечении.

\

Пример задачи с решением.

С. Задача 5

Построить линии влияния внутренних усилий для многопролетной балки.

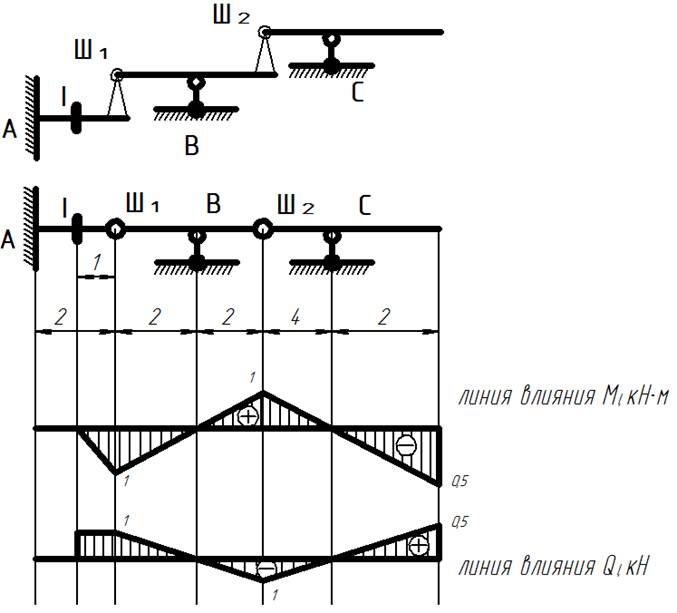
Линии влияния для многопролетной балки

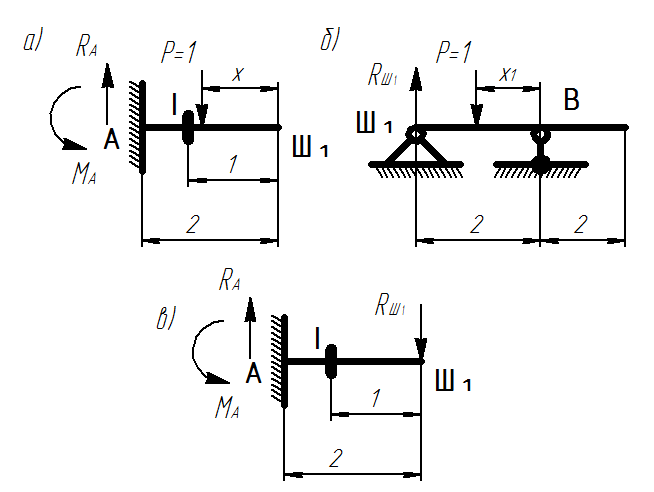
Схемы для построения линий влияния

1) Определяем реакции в опорах балки с сечением I (рис. а):

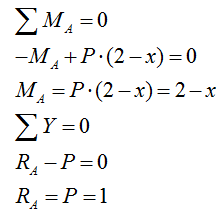
2) Рассматриваем случай расположения силы Р=1 справа от сечения I:

Рассматриваем характерные точки: x=0; 1.

При этом рассматриваем действие сил, лежащих левее сечения I.

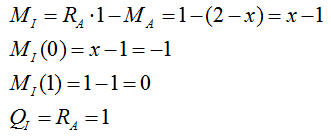
3) Рассматриваем случай расположения силы Р=1 слева от сечения I:

Рассматриваем характерные точки: x=1; 2.

При этом рассматриваем действие сил, лежащих правее сечения I.

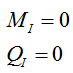
4) Определяем реакцию в шарнире вспомогательной балки Ш₁B, примыкающем к балке с сечением (рис. б):

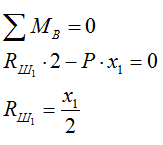
5) Определяем реакции в опорах балки с сечением I с учетом реакции Rш₁ (которую переносим на балку с сечением, меняя направление) (рис. в):

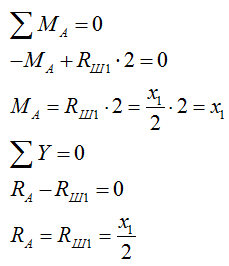
6) Рассматриваем случай расположения силы Р=1 на вспомогательной балке (справа от сечения I):

Рассматриваем характерные точки: x₁=0; 2; -2.

При этом рассматриваем действие сил, лежащих левее сечения I.

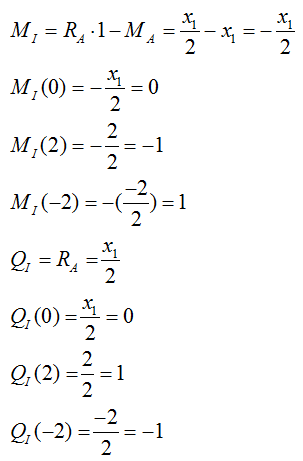
Далее расчет ведется по аналогии на базе пунктов 4-6 (рассматриваем расположение силы Р=1 на вспомогательной балке Ш₂С).

С. Задача 6

Построить линии влияния внутренних усилий для многопролетной балки.

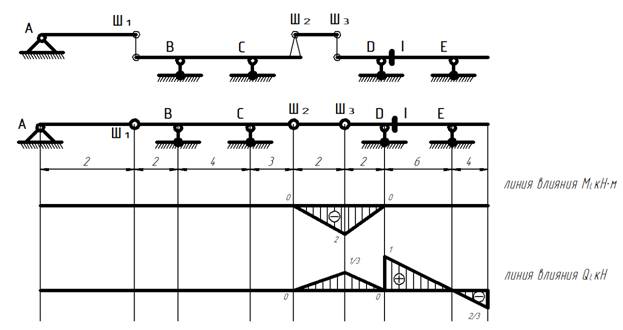
Линии влияния для многопролетной балки

Линия влияния для балки с сечением строится как показано в примерах выше.

Линии влияния для вспомогательных балок имеют значение 0 в опорах. И могут быть построены графически. Значения на линиях влияния определяются из условия подобия треугольников:

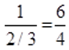
С. Задача. Метод матриц

Построить эпюры внутренних усилий и линии влияния для указанного сеченияметодом матриц.

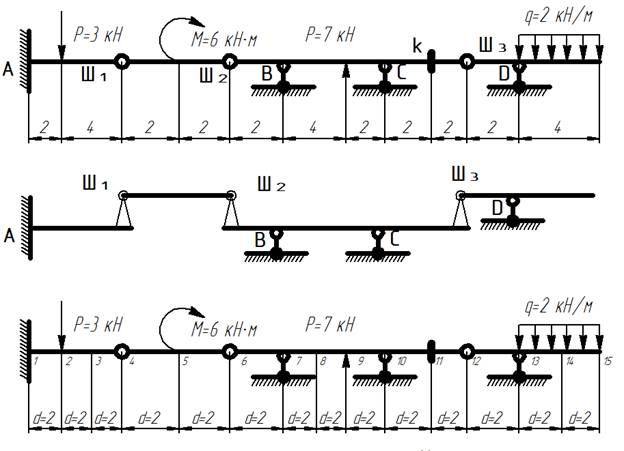
Расчет многопролетной балки методом матриц

1) Разбиваем балку на равные участки и пронумеруем их границы. При этом точки разбиения балки должны приходится на точки приложения внешних нагрузок, связей в балке.

2) Рассчитываем сосредоточенные силы в каждой точке. Для этого каждый участок рассматриваем как отдельную балку и определяем для нее реакции от внешних нагрузок. На границе двух участков суммируем реакции, направляя полученный результат в противоположную сторону, и определяем сосредоточенную силу в точке на границе двух участков.

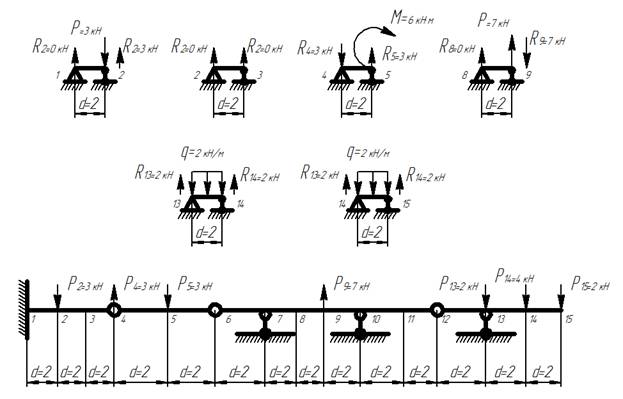
Расчет сосредоточенных сил

3) Составляем матрицу нагрузки Р (положительное направление принимаем для силы, направленной вниз):

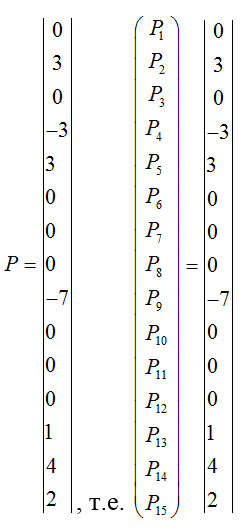
4) Построим эпюры изгибающих моментов для многопролетной балки для случаев нахождения силы Р=1 в каждой введенной точке.

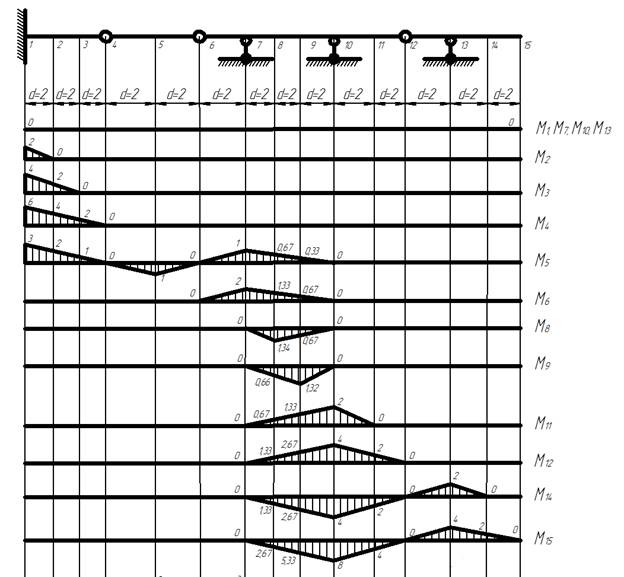
Эпюры изгибающих моментов от силы Р=1

5) Составляем матрицу влияния моментов L_M, каждый столбец которой представляет собой ординаты построенных эпюр изгибающих моментов в введенных точках:

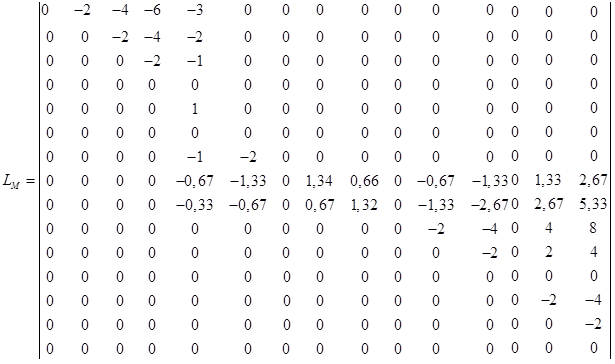
, т.е.:

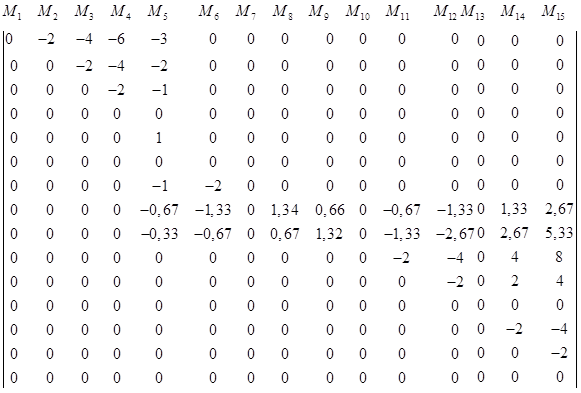
6) Составляем матрицу влияния поперечных сил L_Q. Для этого воспользуемся матрицей перехода K_QM от матрицы L_M к L_Q.

Матрица K_QM имеет туже размерность, что и матрица L_M (в данном примере 15×15).

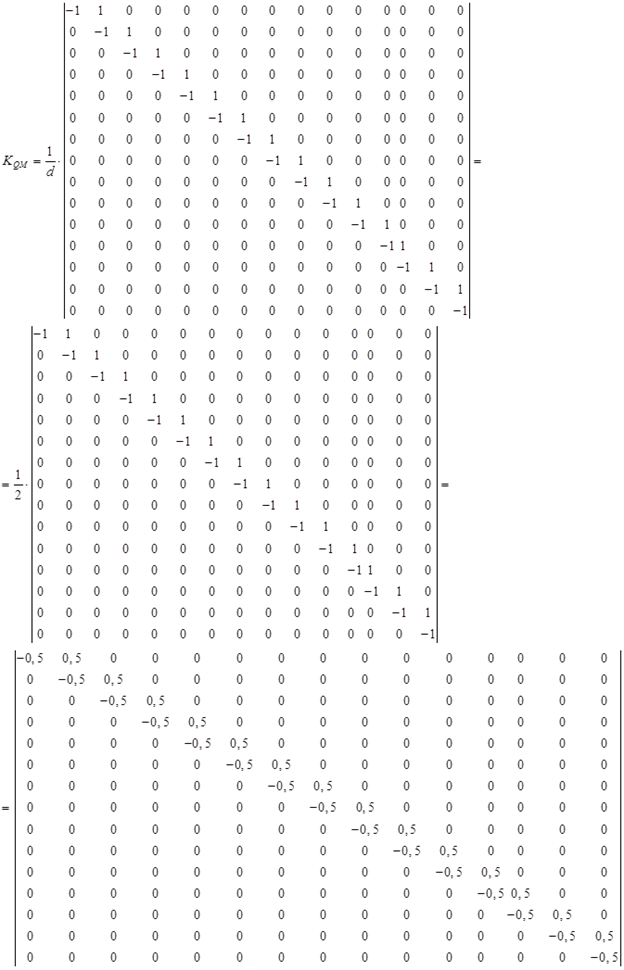
где d – длина участков, на которые разбита многопролетная балка.

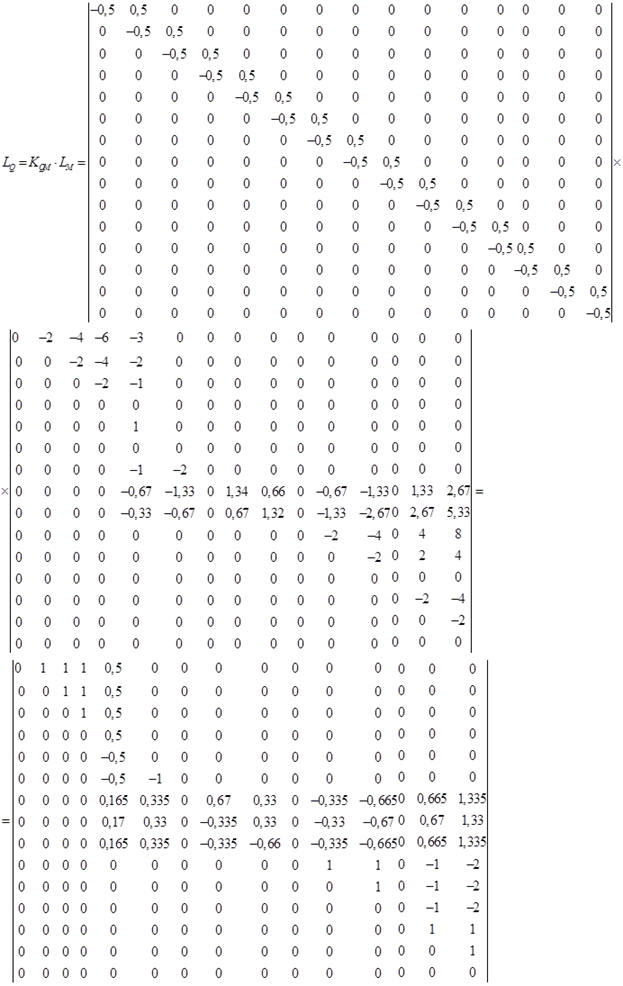
7) Составляем матрицу изгибающих моментов М:

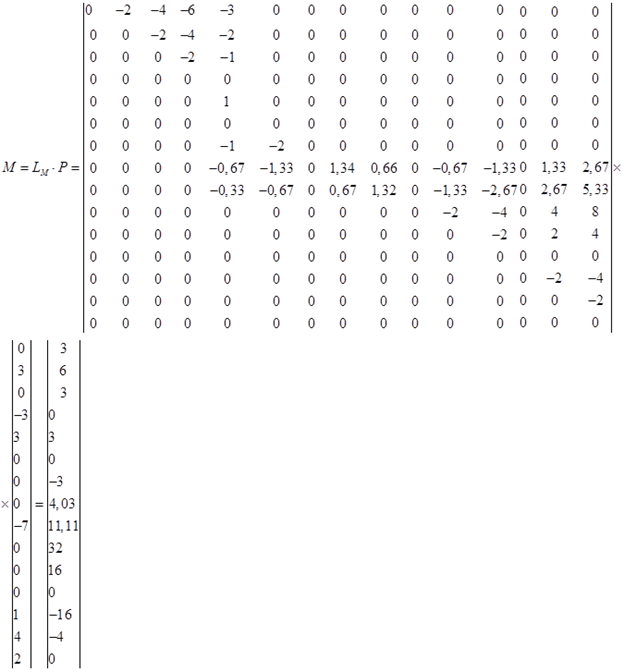
8) Составляем матрицу поперечных сил Q:

9) Строим эпюры изгибающих моментов М и поперечных сил Q. Для этого полученные величины матриц М и Q откладываем в введенных точках. При этом для участка с распределенного нагрузкой необходимо значения эпюры, построенной из матрицы, сложить с эпюрой от распределенной нагрузки в пределах каждого участка с распределенного нагрузкой, рассматривая этот участок как самостоятельную балку на опорах (рисунок 1). При построении эпюр учитываем, что под сосредоточенным моментом должен быть скачок на его величину на эпюре изгибающих моментов, а на эпюре поперечных сил его быть не должно.

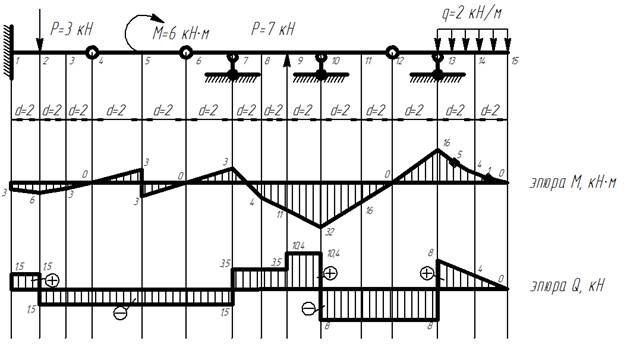
Эпюры внутренних усилий

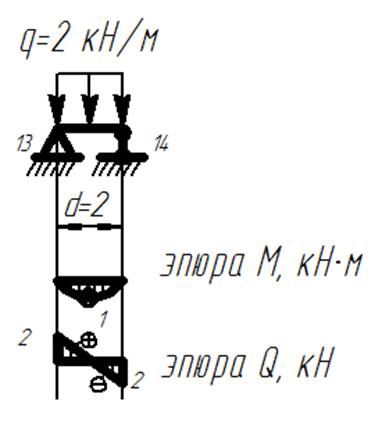
Рисунок 1. Эпюры внутренних усилий для участка с распределенной нагрузкой

10) Построение линий влияния изгибающего момента М и поперечной силы Q.

Каждая строка матриц L_M и L_Q содержит ординаты линии влияния для соответствующего сечения, проходящего через введенную точку.

Заданному сечению, находящемуся в 11 введенной точке соответствуют 11 строки матриц L_M и L_Q.

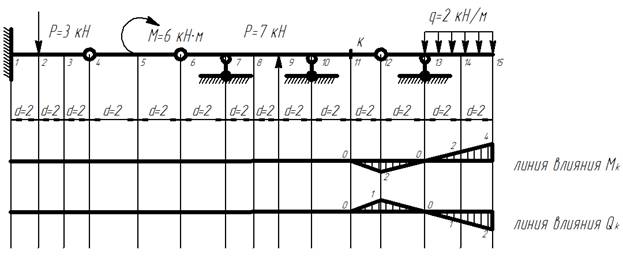
Линии влияния для сечения k

11) Определяем изгибающий момент М и поперечную силу Q в сечении k по линиям влияния:

- изгибающий момент М_k:

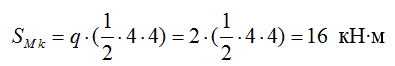
- поперечная сила Q_k:

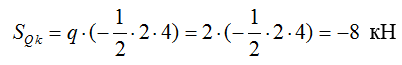
Полученные значения соответствуют значениям на эпюрах в сечении.

Расчет рам

Принципы расчет простой рамы аналогичен расчету простой балки. Единственным отличием является появление горизонтальных реакций в опорах даже от вертикальных нагрузок.

Количество степеней свободы плоской стержневой системы определяется по формуле, называемой основной формулой кинематического анализа:

W = 3Д – 2Ш – С₀

При W=0–система неизменяема и статически определима (т.е. может быть решена путем составления уравнений равновесия).

Для определения реакций в опорах применяетсяпринцип освобождения от связей – систему можно освободить от связей, если эти связи (например, опоры) заменить реакциями. Далее составив уравнения равновесия для новой полученной системы определяют величины введенных реакций.

Уравнения равновесия для плоской системы можно составить в следующих видах:

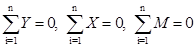
В элементах стержневой системы на плоскости могут возникать три вида внутренних усилий: продольная сила N,поперечная сила Q, изгибающий момент M. Положительные значения указанных усилий в зависимости от направления внутренних усилий определяются как на рис. 1:

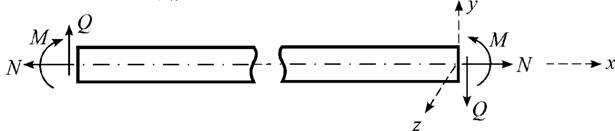
Рисунок 1. Правило знаков для внутренних усилий

Правила для проверки правильности построения эпюр:

1. На участках стержня, на которые действует равномерно распределенная нагрузка q эпюра изгибающих моментов М имеет вид выпуклой (вогнутой) кривой (выпуклость это кривой направлена в ту сторону, куда и направлена распределенная нагрузка), эпюра Q – наклонной прямой.

2. В местах расположения на стержне сосредоточенной силы P на эпюре поперечной силы Q всегда будет перепад на величину этой сосредоточенной силы. В месте расположениясосредоточенного момента на эпюре изгибающих моментов М также всегда будет перепад на величину этого сосредоточенного момента.

Расчет составной рамы

Составные рамы представляют собой статически определимые геометрически неизменяемые распорные системы. Характерной особенностью распорных систем является наличие горизонтальных составляющих опорных реакций при действии вертикальной нагрузки. Для определения реакций в таких системах составляют два уравнения моментов относительно опорных шарниров и два – относительно ключевого шарнира. Проверкой правильности нахождения реакций служат уравнения равновесия – сумма проекций всех сил на оси X и Y.

При составлении уравнений относительно ключевого шарнира рассматриваются отдельно левая и правая части рама, разделенные ключевым шарниром.

Если составную раму можно разделить на основную – статически определимую геометрически неизменяемую раму, и вспомогательную (приставную) раму, прикрепленную к основной при помощи шарнира, то ее расчленяют на отдельные рамы по шарниру, вместо которого прикладывают два неизвестных усилия (горизонтальное и вертикальное), причем расчет начинают вести со вспомогательной (приставной) рамы.

С. Задача 1

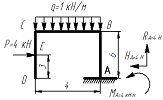
Построить эпюры внутренних усилий для простой рамы.

Подробнее: С. Задача 1

С. Задача 2

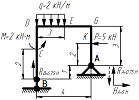
Построить эпюры внутренних усилий для простой рамы.

С. Задача 1

Построить эпюры внутренних усилий для составной рамы.

Данную раму разделить на основную (статически определимую и геометрически неизменяемую) и вспомогательную нельзя. Поэтому рассчитываем ее как неделимую систему.

Подробнее: С. Задача 1

С. Задача 1

Построить эпюры внутренних усилий для простой рамы.

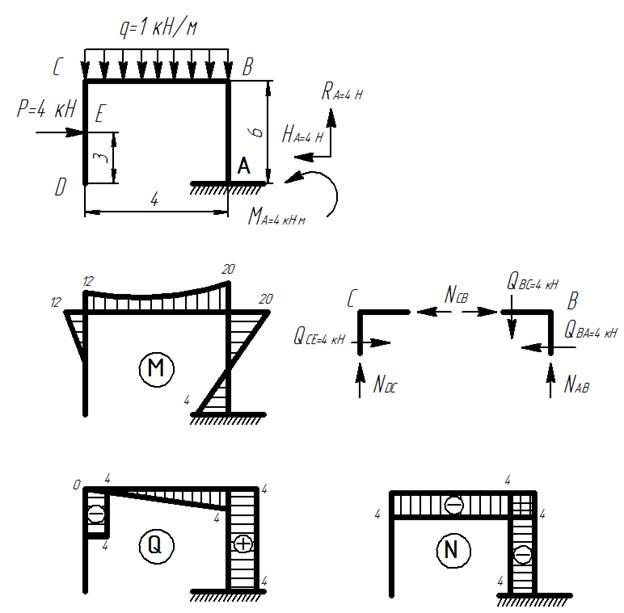
Простая рама

1) Определяем реакции в опорах:

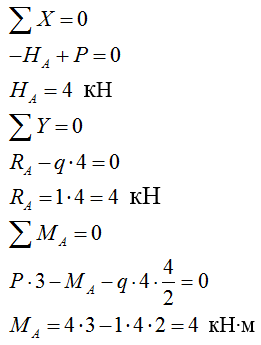
2) Строим эпюру изгибающих моментов М (построение ведем с любого "свободного" конца рамы):

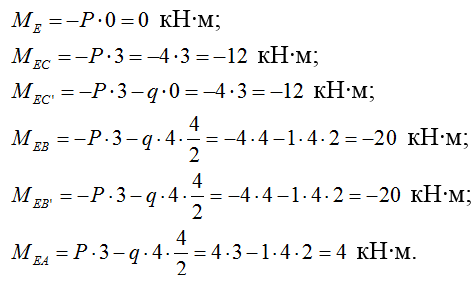
3) Строим эпюру поперечных сил Q (формула Журавского):

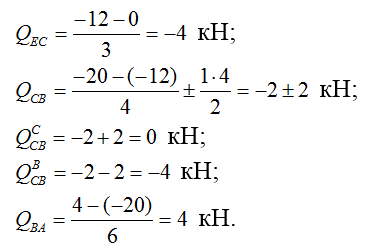
4) Строим эпюру продольных сил N методом вырезания узлов:

Рассматриваем узел С:

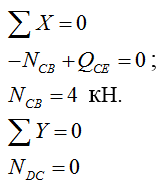
Рассматриваем узел B:

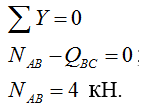
С. Задача 2

Построить эпюры внутренних усилий для простой рамы.

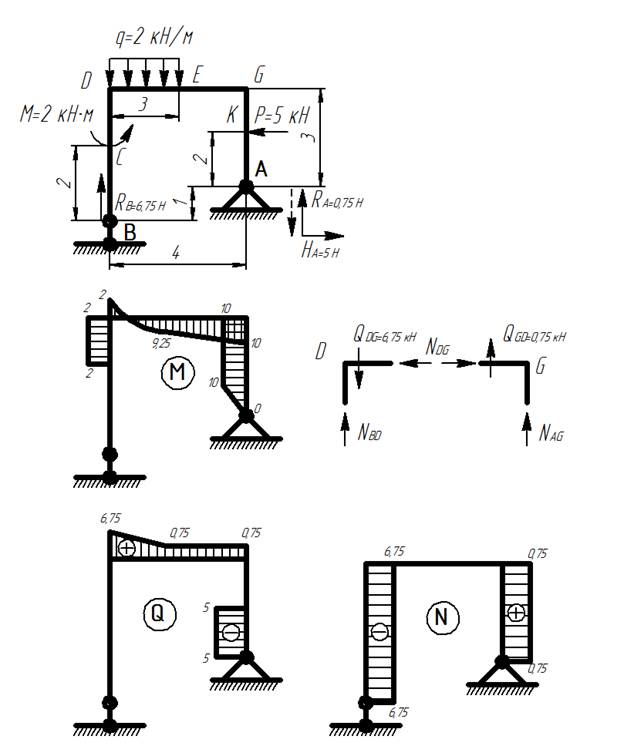
Простая рама

1) Определяем реакции в опорах:

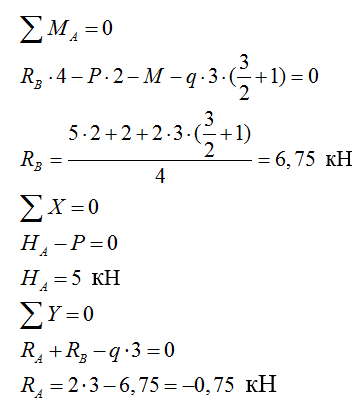
2) Строим эпюру изгибающих моментов М:

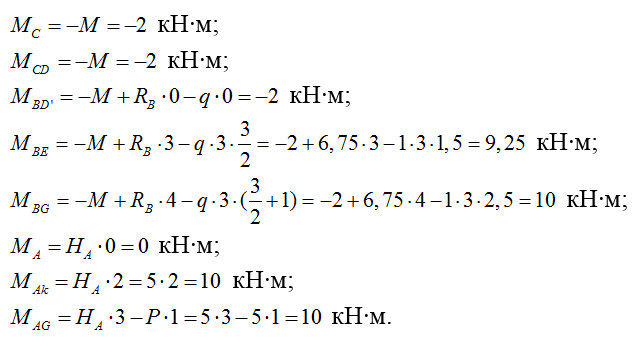
3) Строим эпюру поперечных сил Q:

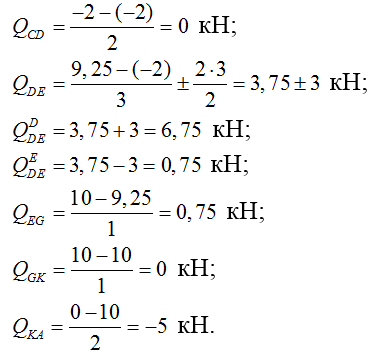
4) Строим эпюру продольных сил N:

Рассматриваем узел D:

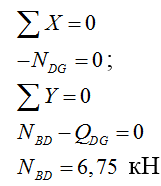
Рассматриваем узел G:

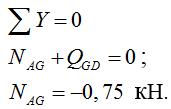
С. Задача 3

Построить эпюры внутренних усилий для простой рамы.

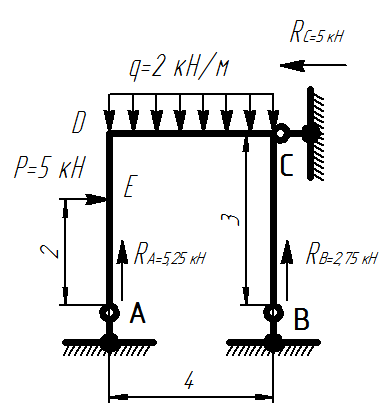
Простая рама

1) Определяем реакции в опорах:

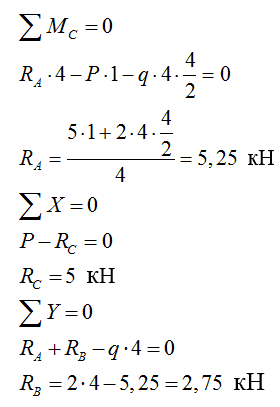
Проверка:

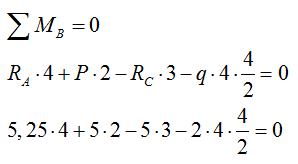
2) Строим эпюру изгибающих моментов М:

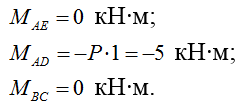
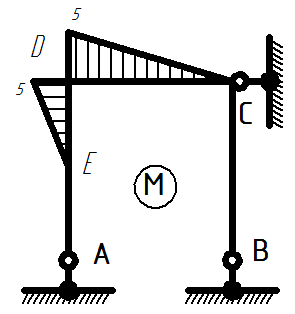
Эпюра изгибающих моментов

3) Строим эпюру поперечных сил Q:

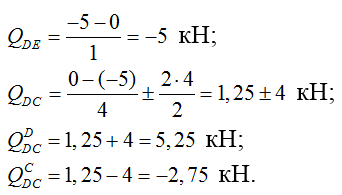
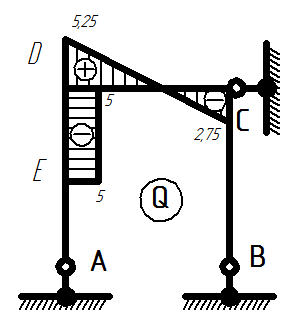
Эпюра поперечных сил

4) Строим эпюру продольных сил N:

Рассматриваем узел D:

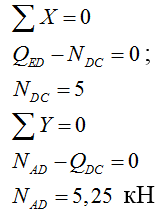
Рассматриваем узел G:

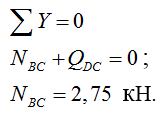
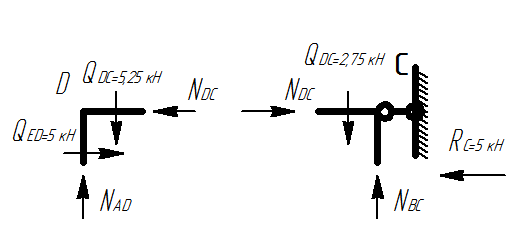
Метод вырезания узлов

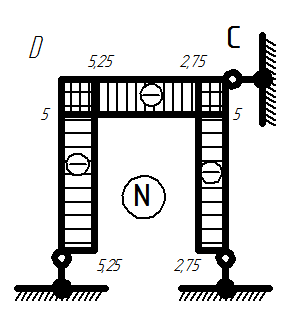
Эпюра продольных сил

С. Задача 4

Построить эпюры внутренних усилий для простой рамы.

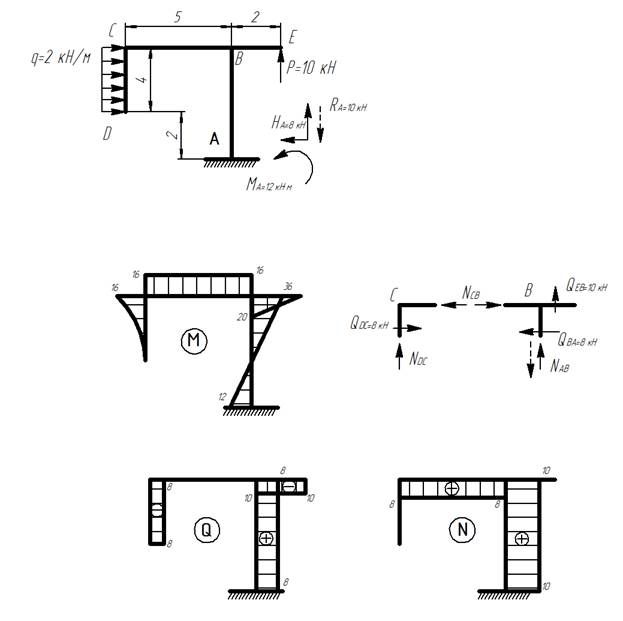
Простая рама

1) Определяем реакции в опорах:

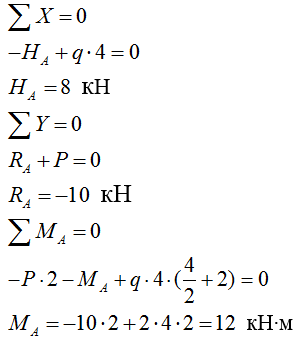
2) Строим эпюру изгибающих моментов М:

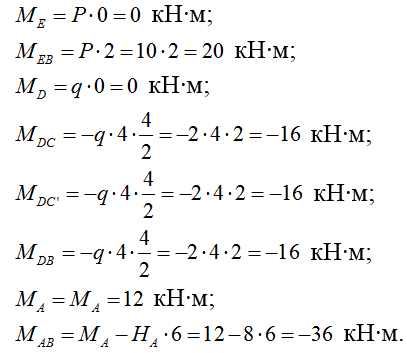
3) Строим эпюру поперечных сил Q:

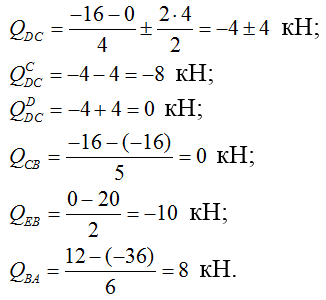
4) Строим эпюру продольных сил N:

Рассматриваем узел D:

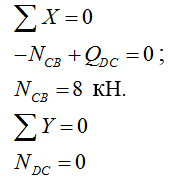
Рассматриваем узел G: