Скорость точки при сложном движении

Докажем теорему о сложении скоростей для сложного движения точки, состоящегоиз относительного движения по отношению к под­вижной системе отсчета Охуz и переносного движения вместе с этой системой в случае, когда подвижная система отсчета связана с твер­дым телом, совершающим произвольное движение в пространстве (рис. 13.4).

Это произвольное движение в механике принято называть общим случаем движения, которое можно разложить на поступательное движение вместе с некоторым полюсом и вращательное движение вокруг этого полюса. В процессе вращения неподвижной остается только одна точка, поэтому такое вращение называется сферическим, а ось вращения, в отличие от обычного вращательного движения, мгновенной, т.к. ее положение в пространстве изменяется со временем.

Таким образом, само переносное движение является сложным, представляющим собой совокупность поступательного движения под­вижной системы вместе с точкой О (полюсом) и сферического движе­ния вокруг этого полюса. Это сферическое движение в каждый момент можно рассматривать как вращение подвижной системы с угловой скоростью 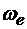вокруг мгновенной оси Ώ, проходящей через полюс О.

Во все время движения точки радиусы-векторы 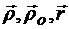связаны зависимостью

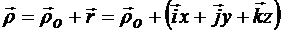. (13.1)

Вектор абсолютной скорости точки

.

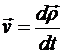Дифференцируя выражение (13.1) и учитывая, что орты 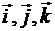подвижной системы Oxyz, оставаясь неизменными по модулю, вра­щаются вокруг мгновенной оси с угловой скоростью 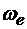, получаем

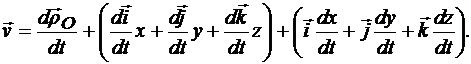(13.2)

Производная от каждого орта по времени представляет собой линейную скорость точки, для которой этот орт является радиусом-вектором (рис. 13.4):

.

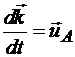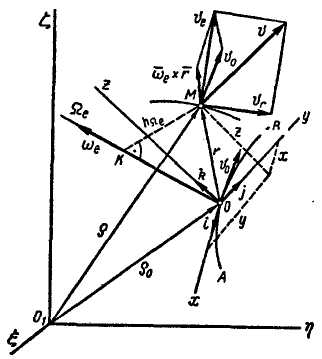
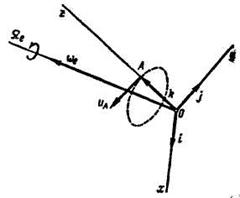
Рис. 13.4 Рис. 13.5

Но каждый орт вращается вокруг мгновенной оси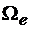, и враща­тельная скорость его конца определяется векторным произведением:

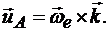
Следовательно,

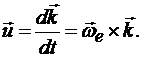
Таким образом

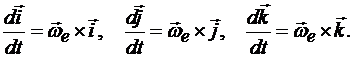(13.3)

Подставляем (13.3) в (13.2):

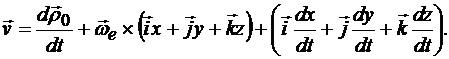
Здесь 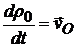- скорость полюса О;

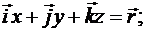
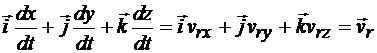- относительная скорость точки М.

Поэтому

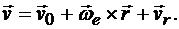(13.4)

Переносная скорость точки, как указывалось ранее, представляет собой скорость точки, связанной с подвижной системой отсчета и совпа­дающей в данный момент с движущейся точкой М. В рассматриваемом случае такой точкой является точка М свободного твердого тела. Ско­рость этой точки состоит из скорости полюса О и вращательной скорости точки вокруг мгновенной осиΏ, т. е.

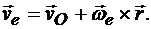(13.5)

На этом основании формула (4) принимает вид

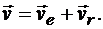(13.6)

Это равенство выражает теорему о сложении скоростей, которая формулируется так: абсолютная скорость точки равна геометрической сумме ее переносной и относительной скоростей.

Эту теорему называют правилом параллелограммаили треуголь­ника скоростей.

Как видно, в рассматриваемом случае сложного переносного дви­жения переносная скорость точки 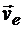, сама определяется как диагональ параллелограмма, построенного на скорости полюса 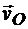и вращательной скорости точки 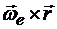вокруг мгновенной оси Ώ_e, (рис. 13.4).

В случае поступательного переносного движения скорости всех точек, неизменно связанных с подвижной системой отсчета, в каждый момент геометрически равны. Поэтому переносная скорость точки М равна скорости полюса 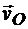и формула (13.5) принимает вид

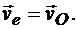
Очевидно, что в этом случае абсолютная скорость точки М также определяется по формуле (13.6).

Так как абсолютная скорость точки 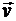определяется диагональю параллелограмма, построенного на переносной скорости 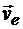, и относи­тельной скорости 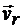, то ее модуль можно вычислить по формуле

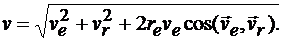(13.7)