Скорость и ускорение точек, вращающегося тела

Выберем произвольную точку М твер­дого тела ( 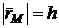), вращающегося вокруг неподвижной оси OZ (рис. 10.5). Движение точки М можно описать радиусом-век­тором 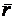, который имеет постоянный мо­дуль для выбранной точки:

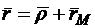. (10.5)

Дифференцируя (10.5) по времени, нахо­дим скорость:

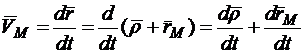, (10.6)

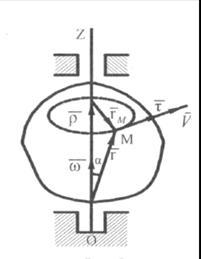
Рис. 10.5

где 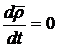, так как вектор 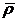постоянен по величине и направлению как производная вектора постоянного модуля по скалярному аргументу.

Тогда

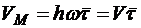, (10.7)

где

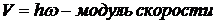. (10.8)

(h — расстояние от точки до оси вращения).

Вектор скорости будет направлен по касательной к траекто­рии точки М в соответствии с направлением угловой скорости.

Пример 4. Точка А, лежащая на ободе диска, имеет скорость 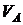= 40 см/с. Точка В, принадлежащая диску, имеет скорость 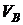= 10 см/с (рис. 10.6). Определить угловую скорость диска и его радиус, если расстояние АВ = 15 см.

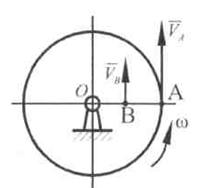
Рис. 10.6

Решение. Применим формулу (8)

,

.

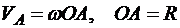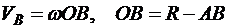Тогда

,

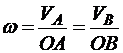пли

,

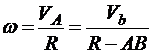откуда

,

,

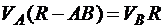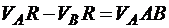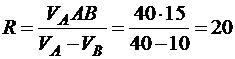см,

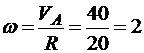рад/с.

Ответ. R=20 см, ω=2 рад/с.

Получим векторную формулу Эйлера для скорости любой точ­ки твердого тела, вращающегося вокруг неподвижной оси. Из рис. 10.5 видно, что 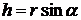. Тогда 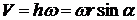. Это выра­жение является модулем векторного произведения 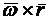, т.е. 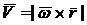. Направление вектора скорости 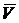определяется век­торным произведением. Следовательно:

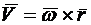. (10.9)

Это выражение называют векторной формулой Эйлера.

Скорость любой точки твердого тела, вращающегося вокруг неподвижной оси, равна векторному произведению вектора угловой скорости на радиус-вектор этой точки, проведенный из произвольной точки на оси вращения.

Определим ускорение точки М:

,

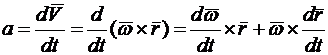так как

,

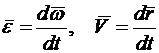то

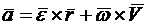. (10.10)

Рассмотрим слагаемые, входящие в это выражение. Вектор 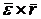в соответствии с правилом векторного произведения направлен по касательной к траектории точки М, т. е. как касательное уско­рение точки М, которое во вращатель­ном движении называют вращательным ускорением (рис. 10.7):

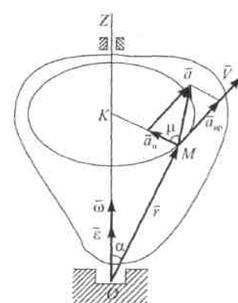
Рис. 10.7

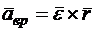. (10.11)

Величина вращательного ускорения

,

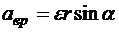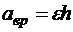. (10.12)

Вектор 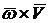находится в плоскости окружности радиуса КМ = h, направлен от точки М к оси вращения и является нормальным ускорением точки М. При вращательном движении это ускорение называют центростремительным ускорением:

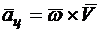. (10.13)

Величина центростремительного ускорения:

,

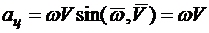где ,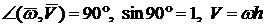

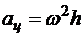. (10.14)

Модуль полного ускорения точки, вращающегося твердого тела

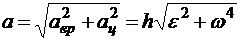. (10.15)

Угол между полным ускорением и центростремительным равен:

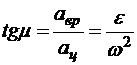. (10.16)

Выражения (10.8) и (10.15) показывают, что скорости и ускорения точек вращающегося твердого тела пропорциональны расстояни­ям от этих точек до оси вращения, а из формулы (10.16) следует, что угол отклонения полного ускорения от центростремительно­го в каждый момент времени один и тот же для всех точек тела.

Уравнение равномерного вращения тела. Вращение тела с постоянной угловой скоростью называется равномерным. Составим уравнение равномерного вращения тела с угловой скоростью ω, принимая направление этоговращения за положительное направление отсчета угла поворота φ.

Положим, что в начальный момент t_o=0 угол поворотаимеет значение φ₀. Тогда

.

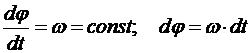Проинтегрируем уравнение в пределах, соответствующих начальному моменту t₀ = 0 и произвольному моменту времени t:

,

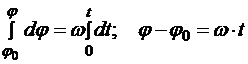откуда

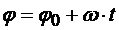(10.17)

Выражение (10.17) является уравнением равномерного вращения тела. Если в начальный момент времени подвижная полуплоскость Q совпадает с неподвижной полуплоскостью Р, т. е. φ₀ = 0, то уравнение равномерного вращения тела (10.17) принимает вид

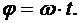
Из уравнения равномерного вращения тела при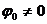

,

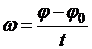т. е. угловая скорость равномерного вращения тела равна отношению приращения угла поворота за некоторый промежуток времени к этому промежутку времени.

Число оборотов, совершаемых вращающимся телом за единицу вре­мени (обычно за минуту), называется частотой вращения и обозна­чаетсяn. Так как один оборот равен 2π радиан, то зависимость между угловой скоростью ω (рад/с) и частотой вращения n (об/мин) имеет вид

, .

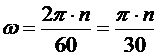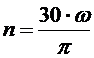Уравнение равнопеременного вращения тела.Вращение тела, при кото­ром угловое ускорение постоянно,называют равнопеременным враще­нием.При этом, если абсолютнаявеличина угловой скорости увеличи­вается, вращениеназывают равноускоренным, иесли уменьшается - равнозамедленным.

Составим уравнение равнопеременного вращения, полагая, что в начальный момент t₀ = 0 начальная угловая скорость 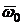, а начальное значение угла поворота φ₀. Тогда

.

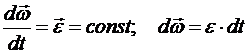Проинтегрируем уравнение в пределах, соответствующих началь­ному моменту t₀=0 н произвольному моменту времени t:

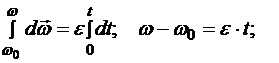
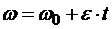,(10.18)

.

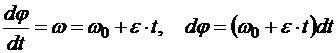Проинтегрируем это уравнение в соответствующих пределах:

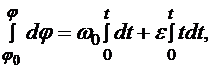
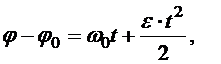
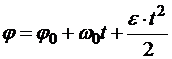. (10.19)

Уравнение (10.19) является уравнением равнопеременного вращения тела.

Так как равнопеременное вращение происходит обычно в одном направлении, то 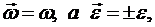где знак плюс соответствует уско­ренному вращению, а знак минус - замедленному. Учитывая это, формулам (18) и (19 можно придать более удобный для решения задач вид:

.

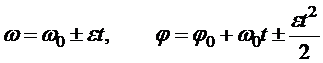Из формулы угловой скорости находим 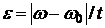, т. е. при равно­переменном вращении абсолютное значение углового ускорения тела равно отношению изменения угловой скорости тела за некоторый промежуток времени к числовой величине этого промежутка.

Пример 5. Вал начинает вращаться равноускоренно из состояния покоя; в первые 20 с он совершает 100 оборотов. Каковы егоугловые скорость и ускорение по истечении 20 с?

Решение. Так как вал начинает вращаться из состояния покое, то ω₀=0. В этом случае при φ₀=0

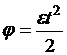,(1)

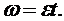(2)

Из уравнения (1) находим

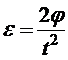, (3)

где .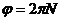

Подставляяв (3) числовые значения, находим

Передаточные механизмы

Передаточные механизмы предназначены для передачи вращения от одною вала. называемого ведущим, к другому, называемому ведо­мым. Если оси ведущего и ведомого валов параллельны или пересекают­ся, то вращение можно передать с помощью фрикционной или зубчатой передачи (рис. 10.8 – 10.11).

Во фрикционной передаче вращение передается вследствие действия силы сцепления на поверхности соприкасающихся колес, в зубчатой передаче - от зацепления зубьев. Вращательная скорость 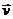в точке соприкасания колес относится к точкам обоих колес, т. е. ее модуль определяется как

.

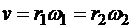откуда

.

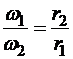Таким образом, угловые скорости колес фрикционной или зубчатой передачи обратно пропорциональны радиусам колес.

Отношение угловой скорости ведущего колеса к угловой скорости ведо­мого колеса называется передаточным числам:

.

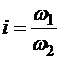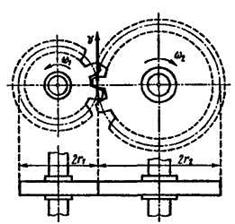
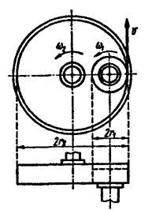
Рис. 10.8 Рис. 10.9

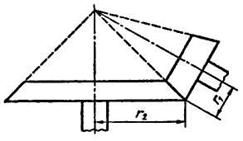
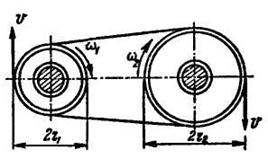
Рис. 10.10 Рис. 10.11

Передаточное число можно вычислить как обратное отношение радиусов колес:

.

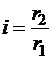Так как числа зубьев пропорциональны длинам окружностей и, следовательно, радиусам, то передаточное число определяется и по числу зубьев:

.

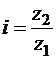При внешнем зацеплении (рис. 10.8) направление вращения ведущего и ведомого колес противоположное, а при внутреннем (рис. 10.9) - одинаковое.

Кроме фрикционной и зубчатой передач существует передача на расстоянии с помощью гибкой связи (ремня, троса, цепи) (рис. 10.11).

Taк как скорости всех точек ремня одинаковы и ремень не скользит по поверхности шкива, то к ременной передаче относятся те же соот­ношения:

.

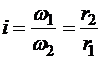Применяются также серии колес с неподвижными осями вращения в виде последовательного ряда с паразитными колесами (рис. 10.12) и последовательного ряда с кратным зацеплением (рис. 10.13), называемые рядовыми соединениями колес.

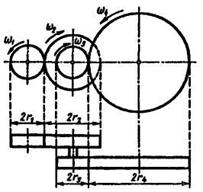
Рис. 10.12 Рис. 10.13

Определим передаточное число фрикционной передачи в виде рядо­вого соединения с паразитными колесами:

для колес 1-2 ;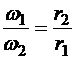

для колес 2-3 .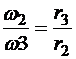

Перемножаем левые и правые части, получаем

.

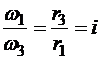Для зубчатых колес

.

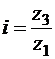Передаточное число рядового соединения с паразитными колесами равно отношению радиусов (чисел зубьев) ведомого и ведущего колес и не зависит от радиусов (чисел зубьев) паразитных колес.

Определим передаточное число рядового соединения с кратным зацеплением.

Частное передаточное число для колес 1-2

.

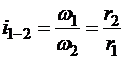Частное передаточное число для колес 3-4

.

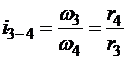Так как колеса 2—3 соединены жестко, т. е. 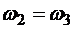то общее передаточное число 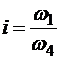равно произведению передаточных чисел:

.

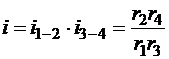Для зубчатых колес

.

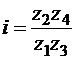Таким образом, общее передаточное число рядового соединения колес с кратным зацеплением равно произведению чисел зубьев ведомых колес, деленному на произведение чисел зубьев ведущих колес.

В рассмотренных выше передачах при равномерном вращении ведущего вала ведомый вал вращается тоже равномерно.

Для получения переменной угловой скорости ведомого вала приме­няются передачи, в которых расстояние от точки соприкасания колес до оси одного из валов или обоих валов изменяется.

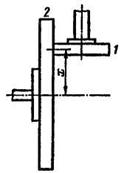
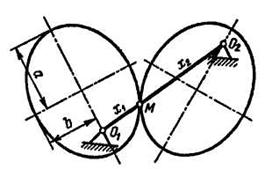
Рис. 10.14 Рис. 10.15

Во фрикционной передаче, изображенной на рис. 10.14, колесо 1 пере­мещается вдоль его оси и отношение угловых скоростей зависит от переменного расстояния х:

.

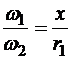На рис.10.15 изображены эллиптические колеса, оси вращения которых находятся в фокусах эллипсов. Отношение угловых скоростей зависит от переменных расстояни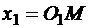й

и ,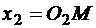

где

.

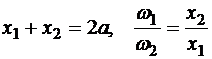Пример 1. Вал начинает вращаться равноускоренно из состояния покоя. В первые 20 с он совершает 100 оборотов. Каковы егоугловые скорость и ускорение по истечении 20 с?

Решение. Так как вал начинает вращаться из состояния покое, то ω₀=0. В этом случае уравнения при 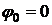имеютвид

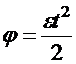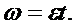, (1)

Из уравнения (1) находим

,

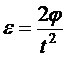где .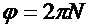

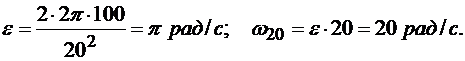
Пример 2. Лебедка (рис. 2.2.1), поднимающая груз по наклонной плоскости, состоит из двух валов 1 л 2 с шестернями (зубчатыми колесами), числа зубьев которых равны соот­ветственно z₁ = 12 и z₂= 48. К валу 2 прикреплен барабан радиусом r= 0,3 м, на который наматывается грузовой трос. Вал 1 вращается равноускоренно с угловым ускоре­нием ε₁ = 8 с^–2. Определить скорость, ускорение и переме­щение груза, а также ускорение точки В барабана в мо­мент времени t = 1 с. В начальный момент времени систе­ма находилась в покое.

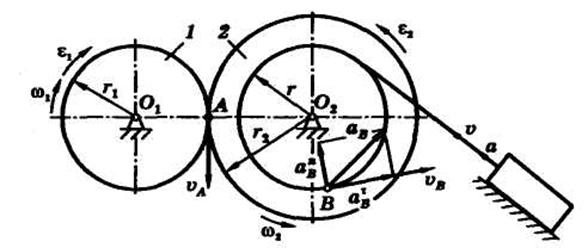
Рис. 2.2.1

Решение. Найдем угловую скорость ω₁ ведущего вала 1 из условия, что оно вращается с угловым ускорени­ем ε₁ = const, учитывая, что 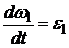. Интегрируя послед­нее уравнение по времени, получаем .

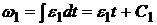Постоянную интегрирования получаем из начального условия: при t= 0 ω₁ = 0 (система находилась в покое), следовательно C₁ = 0.

Итак, угловая скорость вала 1 определяется уравнени­ем .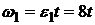

При t = 1 с получаем .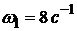

Шестерни 1 и 2 взаимодействуют без проскальзыва­ния. Поэтому скорости точек их касания (точка А) будут одинаковы: .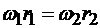

Отсюда находим угловую скорость ω₂ вала 2, учитывая, что :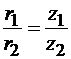

.

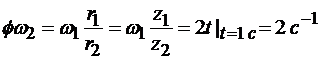Угловое ускорение вала 2 равно .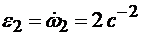

Поскольку трос нерастяжим и относительно барабана не проскальзывает, то скорость груза v будет равна скоро­сти любой из точек на ободе барабана, в частности, скоро­сти точки В: v = v_B = ω₂r = 0,6t=|_{t=1 c} =0,6 м/с.

Ускорение точки В равно векторной сумме касатель­ного (вращательного) и нормального (центростремитель­ного) ускорений: .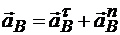

Направление вращательного ускорения определяется направлением углового ускорения ε₂, а его модуль равен 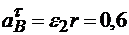м/с². Центростремительное ускорение на­правлено к оси вращения вала 2 и равно по модулю 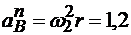м/с².

Модуль ускорения точки В

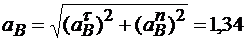м/с².

Ускорение груза можно найти, взяв производную по времени от его скорости, так как это касательное ускоре­ние: 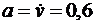м/с².

Перемещение груза определяется интегрированием модуля скорости по времени:

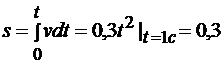м.

Ответ: v = 0,6 м/с; а = 0,6 м/с²; s = 0,3 м; а_B = = 1,34 м/с².

Пример 3. Маховик радиусом R = 0,5 м вращается так, что его угловая скорость меняется в соответствии с уравнением 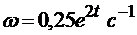. Для момента времени t = 0,5 с после нача­ла движения определить скорость и ускорение точки на ободе маховика. Установить, за какое время маховик сде­лает 100 полных оборотов.

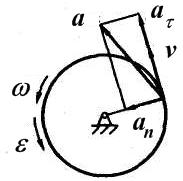
Рис. 2.2.2

Решение. Для момента времени t = 0,5 с получаем ω = 0,680 с^–1, и скорость точки на ободе маховика равна v = ωR = 0,340 м/с.

Угловое ускорение маховика

.

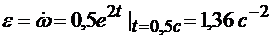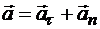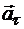Ускорение точки на ободе маховика равно сумме двух составляющих ускорений: , где и 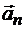— каса­тельное (вращательное) и нормальное (центростремитель­ное) ускорения точки.

Учитывая, что вращательное ускорение равно по мо­дулю 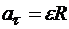, найдем 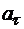=0,680 м/с²; центростремительное ускорение 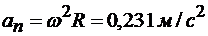. Модуль полного ускорения точки

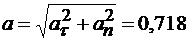м/с.

Направления скорости и ускорений по­казаны на рис. 2.2.2.

Поскольку значения величин угловой скорости и углового ускорения имеют одинаковые знаки, вращение тела уско­ренное. Соответственно, совпадают по направлению угловая скорость и угловое ускорение тела, а также скорость точки и вращательное ускорение.

Поворот маховика на 100 полных оборотов соответ­ствует углу его поворота φ = 200π рад. Выражение для угла поворота найдем из уравнения .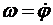

Имеем

.

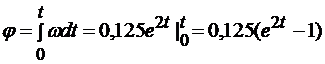Итак, 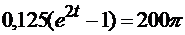, откуда находим t = 2,19 с.

Пример 4.Вращение маховикав периодпуска машины определяется уравнением 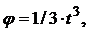где t–в с, φ - в рад. Определить модуль и направление ускорения точки, отстоящей от оси вращения на расстоянии 50 см, в тот момент, когда ее ско­рость равна 8 м/с.

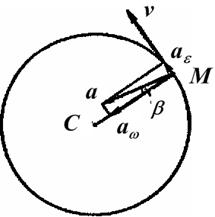
Рис. 2.2.3

Решение. По уравнению вращения маховика находим его угловые скорость и ускорение согласно формулам:

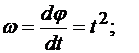(1)

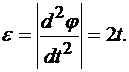(2)

Пользуясь формулой, находим момент времени t₁, когда скорость точки М равна 8 м/с:

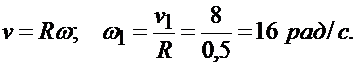
По этому значению 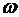из (1) находимt₁:

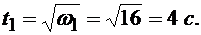
По уравнению (2) вычисляем ε, а затем по формулам модуливращательного, центростремительногои полного ускорений точки М в этот момент времена:

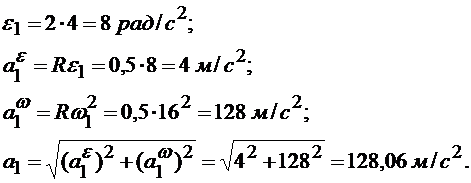
Как видно, модуль полного ускорения точки весьма мало отличается от модуля центростремительного ускорения точки (рис. 2.2.3).

Направление ускоренияточки определяетсяуглом β, образованным уско­рениеми радиусом СМ:

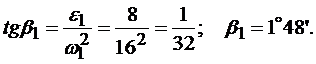
Пример 5. Груз А, подвешенный к нити АВ, намотанной на барабан, опу­скается равноускоренно из состояния покоя, приводя во вращение барабан. За первые 3 с барабан совершает 9 оборотов. Определить в конце 5-й секунды скорость и ускорение точки обода барабана, а также груза А, если диаметр барабана D = 30 см (рис. 2.2.4, а).

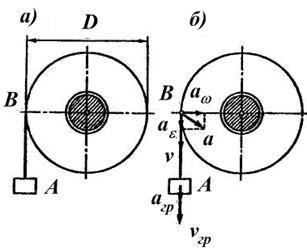
Рис. 2.2.4

Решение. Барабан вращается равноускоренно согласно уравнению:

.

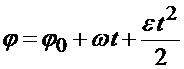Формула угловой скорости имеет вид:

.

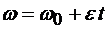Для того чтобы начальное значение угла поворота 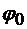было равно нулю, следует неподвижную полуплоскость поместить в начальном положении под­вижной полуплоскости, вращающейся с барабаном. Выполним это и получим .

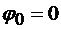При вращении из состояния покоя начальная угловая скорость барабана равна нулю 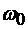. При этих условиях

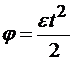; (1)

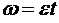. (2)

Так как при t = 3 с 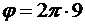рад, то из уравнения (1) определим угловое ускорение :

.

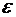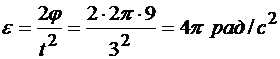Из уравнения (2) найдем угловую скорость барабана в конце 5-й секунды:

.

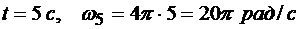Определим в точке В обода барабана (рис. 2.2.4, б) модули вращательной скорости, вращательного и центростремительного ускорений в этот же момент времени по формулам:

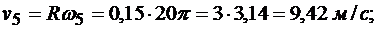
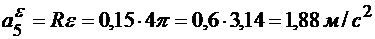
(модуль вращательного ускорения точки тела при равнопеременном вращении одинаков для всех моментов времени);

.

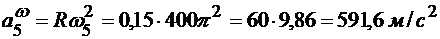Модуль полного ускорения точки обода барабана определяется по формуле:

.

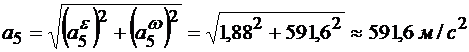Вследствие незначительной величины модуля вращательного ускорения по сравнению с модулем центростремительного ускорения полное ускорение прибли­женно равно центростремительному.

.

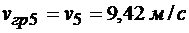Ускорение груза (рис. 2.2.4, б) равно вращательному ускорению точки обода:

.

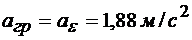Пример 6. Центробежный регулятор вращается с постоянной угловой скоростью ω вокруг вертикальной оси. Угол АСВ равен 60^о, а ускорение шаров А и В равно по величине 100g, где g=980 см/с². Стержни АС, ВС, АD и BD одинаковой длины l=10 см. Сколько оборотов в минуту делает регулятор (рис. 2.2.5)?

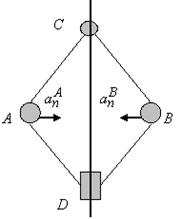
Рис. 2.2.5

Решение. Для того чтобы найти величину угловой скорости регулятора, напишем зависимость ускорения шара от параметров регулятора. Так как регулятор вращается с постоянной скоростью, то ускорение шара будет центростремительным ускорением, модуль которого определяется формулой

,

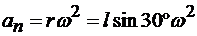где r – кратчайшее расстояние шара до оси вращения.

С другой стороны, согласно условию, 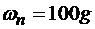. Приравнивая эти два выражения нормального ускорения шара, находим:

.

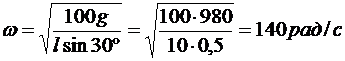Угловая скорость регулятора будет равна

.

Лекция 11