Скорость и ускорение точки при векторном

СПОСОБе ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ

Определение скорости точки

Скорость — это векторная величина, характеризующая быстроту и направление движения точки в данной системеотсчета.

При векторном способе задания движения положение движущейся точки в каждый момент времени определяется радиусом-вектором 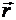, который является функцией времени 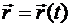. Пусть в момент времени t точка занимает положениеМ, определяемое радиусом-вектором 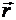, а в момент 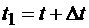- положение M₁, определяемое радиусом-век­тором 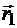(рис. 8.6). Из треугольника ОММ₁,

.

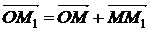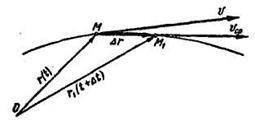
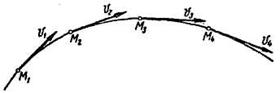
Рис. 8.6 Рис. 8.7

При перемещении точки ее радиуc-вектор получает приращение:

.

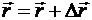Из двух последних равенств следует, что вектор перемещения точки 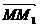является приращением радиуса-вектора точки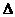 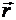за промежу­ток времени 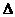t.

Отношение вектора перемещения 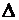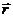к промежутку времени 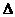t,втечение которого произошло это перемещение, представляет собой вектор средней скорости 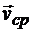воображаемого движения точки по хорде ММ₁:

.

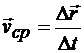Направление вектора 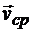совпадает с направлением Δ 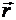. При умень­шении промежутка времени Δt и приближении его к нулю вектор Δ 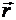также стремится к нулю, а вектор 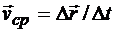- к некоторому пределу. Этот предел является вектором скорости точки в момент t:

.

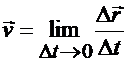Так как Δt - приращение скалярного аргумента t, а Δ 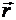- прираще­ние вектора-функции 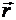, то предел отношения 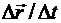при 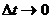явля­ется векторной производной от 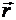по t:

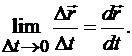
Отсюда

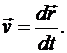
Таким образом, вектор скорости точки в данный момент равен производной от радиуса-вектора точки по времени.

Вектор 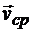направлен по хорде MM₁ в сторону движения точки. Когда Δt стремится к нулю, точка M₁ стремится к точке М, т. е. предельным положением секущейMM₁ является касательная.

Из этого следует, что вектор скорости точки 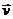направлен по касательной к траектории в сторону движения точки.

При движении точки по криволинейной траектории направление вектора скорости непрерывно изменяется (рис. 8.8).

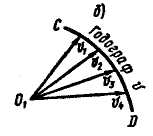
Рис. 8.8

Скорость точки при неравномерном криволинейном движении изменяется как по модулю, так и по направлению.

Отметим ряд положений движущейся точки на траектории M₁, M₂, M₃, М₄ и покажем в этих положениях скорости точки 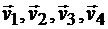(рис. 8.8,а).

Выбрав в пространстве некоторую неподвижную точку О₁, отло­жим от этой точки векторы, геометрически равные скоростям 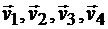(рис. 8.8,б). Если от точки О₁ отложить скорости, соответствующие всем поло­жениям точки М на кривой АВ, и соединить концы этих векторов, то получится линия CD, являющаяся годографом скорости.

Таким образом, годограф скорости представляет собой геометри­ческое место концов векторов скорости движущейся точки, отложен­ных от одной и той же произвольной точки пространства.

Изобразим на рис. 8.9, а траекторию точки АВ и ее скорость 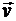в произвольный момент времени t, а на рис. 8.9, б - годограф ско­рости CD этой точки.

Проведем через точку О₁ оси координат X, Y,Z, параллельные основным осямх,y,z. Тогда радиусом-вектором любой точки N годографа скорости CD будет скорость 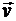, а координаты точек годографа X, У, Z будут равны проекциям скорости на оси координат:

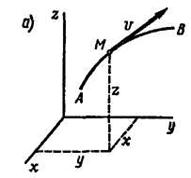
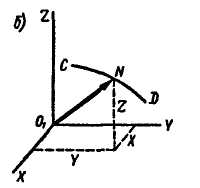
Рис. 8.9

.

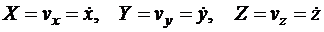Эти уравнения являются параметрическими уравнениями годографа скорости.

Определение ускорения точки

При неравномерном криволинейном движении точки изменяются модуль и направление ее скорости. Ускорение точки характеризует быстроту изменения модуля и направления скорости точки.

Допустим, что в момент времени t точка занимает положение М и имеет скорость 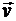, а в момент времени 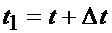она занимает положение M₁ и имеет скорость 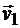(рис. 8.10, а).

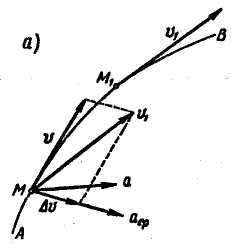
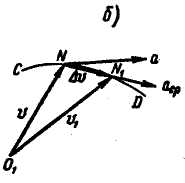
Рис. 8.10

Найдем приращение вектора скорости за промежуток времени Δt. Для этого отложим от точки М скорость 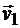и построим при этой точке параллелограмм, одной из сторон которого будет скорость 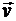, а диагональю - скорость .

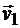Тогда вторая сторона параллелограмма будет приращением вектора скорости 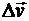, так как

.

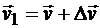Разделив приращение вектора скорости 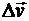на промежуток времени Δt, получим вектор среднего ускорения точки за этот промежуток:

.

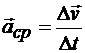Этот вектор имеет направление 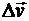и, следовательно, направлен в cторону вогнутости кривой. Построив годограф скорости CD (рис. 13,б), отложим там же скорости v и v₁, приращение вектора скорости 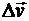, а также вектор среднего ускорения 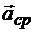, направленный по хорде NN₁ годографа ско­рости. Предел, к которому стремится вектор среднего ускорения 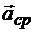, когда Δt стремится к нулю, является вектором ускорения точки α в данный момент времени t:

.

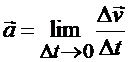Учитывая, что скорость является вектор - функцией от времени, т. е. 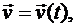и что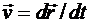

.

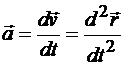Следовательно, вектор ускорения точки равен первой производной от скорости или второй производной от радиуса-вектора точки по времени.

Установим направление вектора ускорения. Вектор среднего ускорения 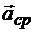направлен по хорде NN₁ годографа скорости. Когда Δt стремятся к нулю, точка N₁ стремится к точке N и секущая NN₁ в пределе превращается в касательную к годографу скорости. Из этого следует, что вектор ускорения точки имеет направ­ление касательной к годографу скорости.

Выясним расположение вектора ускорения точки по отношению к ее траектории, если траектория не является плоской кривой. Вектор 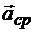находится в плоскости, проходящей через касательную к траектории точке М и прямую, параллельную касательной в точке М₁ (рис. 10,а). Предельное положение этой плоскости при стремлении точки M₁ к точке М называется соприкасающейся плоскостью.

Из этого следует, что вектор ускорения точки 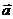расположен в соприкасающейся плоскости и направлен в сторону вогнутости кривой.

Если кривая плоская, то соприкасающейся плоскостью является плоскость кривой и вектор ускорения лежит в этой плоскости.