Для произвольной плоской системы сил можно составить три уравнения равновесия.
Первая форма уравнений равновесия:
1. 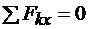 .
.
2. 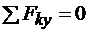 .
.
3. 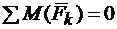 .
.
Третье уравнение составляют относительно произвольной точки. Лучше всего брать точку, в которой имеется больше неизвестных реакций.
Вторая форма уравнений равновесия:
1. 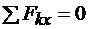 .
.
2. 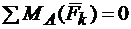 .
.
3. 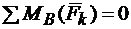 .
.
При использовании второй формы уравнений равновесия необходимо, чтобы ось х не была перпендикулярна прямой АВ.
Третья форма уравнений равновесия:
1. 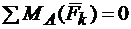 .
.
2. 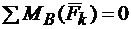 .
.
3. 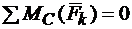 .
.
При использовании третьей формы уравнений равновесия необходимо, чтобы точки А, В, С не лежали на одной прямой.
Задача 8.Определить реакции опор, если F = 10 кН, q = 2 кН/м, М = 3 кНм (рис. 4.7).
Решение. Рассмотрим равновесие балки АВ под действием силы 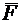 , момента
, момента 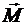 , равномерно распределенной нагрузки и реакций связей
, равномерно распределенной нагрузки и реакций связей 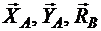 .
.
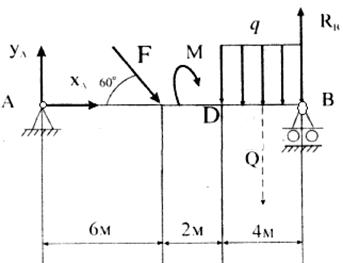
Рис. 4.7
Составим три уравнения равновесия по первой форме. Равномерно распределенную нагрузку заменим равнодействующей 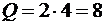 кН, которая приложена в середине участка BD:
кН, которая приложена в середине участка BD:
1. 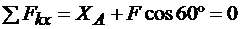 .
.
2. 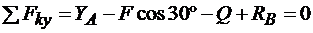 .
.
3. 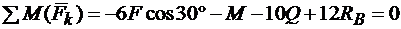 .
.
Находим из (1)
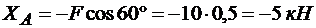 ,
,
из (3)
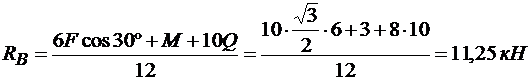 ,
,
из (2)
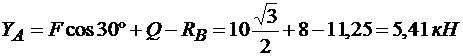 .
.
Ответ. 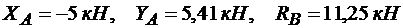
Минус показывает, что направление  противоположно направлению, показанному на рис. 4.7.
противоположно направлению, показанному на рис. 4.7.
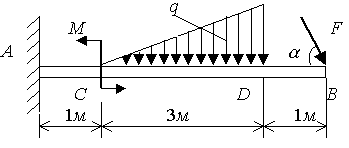
Задача 9. На балку с защемленным концом (рис. 4.2.1, а) действует распределенная по линейному закону нагрузка интенсивностью q = 0,2 кН/м. Сила F = 10 кH действует под углом α = 450 к оси балки, кроме того, приложена пара сил с моментом М = 4 кH∙м. Определить реакцию заделки.
Решение.1. Составление расчетной схемы (рис. 4.2.1, б). Объектом равновесия является балка АВ. К ней приложены активные силы 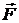 , пара сил с моментом
, пара сил с моментом 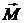 ираспределенная по линейному закону нагрузка. Равнодействующая
ираспределенная по линейному закону нагрузка. Равнодействующая 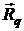 приложена в точке О,
приложена в точке О,
Связью, наложенной на балку АВ,является жесткая заделка А. Применяя принцип освобождаемости от связей к балке АВ,заменим действие этой заделки на балку силами реакций 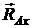 и
и 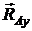 реактивным моментом
реактивным моментом 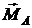 . Рассмотрим теперь равновесие балки АВ как свободного твердого тела, на которое действуют, кроме активных сил, еще и реакции связи.
. Рассмотрим теперь равновесие балки АВ как свободного твердого тела, на которое действуют, кроме активных сил, еще и реакции связи.
2. Условия равновесия:
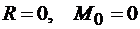 .
.
а)
б)
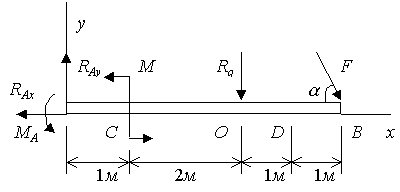
Рис. 4.2.1
3. Составление уравнений равновесия. Для плоской произвольной системы сил условиям равновесия соответствуют три уравнения:
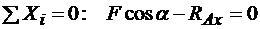 ; (а)
; (а)
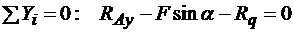 ; (б)
; (б)
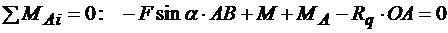 . (в)
. (в)
Для балки с жёсткой заделкой в качестве моментальной точки лучше брать заделку, что позволит исключить лишние неизвестные.
4. Определение искомых величин, проверка правильности решения и анализ полученных результатов.
Из уравнения (а) находим:
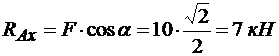 .
.
Из уравнения (б) получаем:
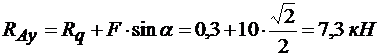 .
. 
Наконец, из уравнения (в) находим:
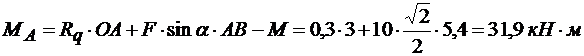
Проверка. Составим уравнение моментов относительно точки В, подставим найденные реакции:
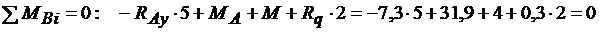 .
.
Положительные значения реакций связей подтверждают правильность выбранных направлений этих сил.
Задача 10. Определить реакции опор А и В балки, находящейся под действием одной сосредоточенной силы и пары сил. Нагрузка и размеры указаны на чертеже (рис. 4.2.2).
Решение.
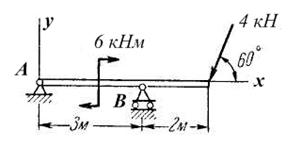
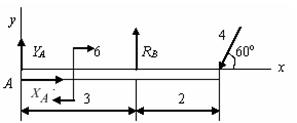
Рис. 4.2.2
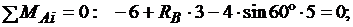
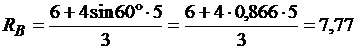 кН,
кН,
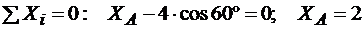 кН
кН
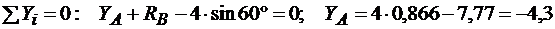 кН.
кН.
