УСЛОВИЯ и уравнения РАВНОВЕСИЯ
РАЗЛИЧНЫХ СИСТЕМ СИЛ
Приведение силы к одному центру
(метод Пуансо)
Пусть даны сила  , приложенная к твердому телу в точке А, и произвольная точка О, которую назовем центром приведения. Проведем из точки О в точку А радиус-вектор
, приложенная к твердому телу в точке А, и произвольная точка О, которую назовем центром приведения. Проведем из точки О в точку А радиус-вектор 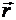 (рис. 4.1, а) и определим момент силы
(рис. 4.1, а) и определим момент силы  относительно центра приведения:
относительно центра приведения:
 .
.



Рис. 4.1
Приложим в точке О две уравновешивающиеся силы 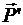 и
и  , равные и параллельные силе
, равные и параллельные силе  (рис. 4.1, б). Получим эквивалентную силе
(рис. 4.1, б). Получим эквивалентную силе  систему трех сил
систему трех сил  ,
, 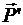 и
и  , которую можно рассматривать как совокупность силы
, которую можно рассматривать как совокупность силы  (
(  =
=  ), приложенной в центре приведения О и присоединенной пары сил
), приложенной в центре приведения О и присоединенной пары сил  ,
, 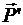 .
.
Опустив из точки О перпендикуляр на линию действия силы  , получим плечо этой пары сил и найдем модуль ее момента равный модулю момента силы
, получим плечо этой пары сил и найдем модуль ее момента равный модулю момента силы  относительно центра приведения О.
относительно центра приведения О.
 ,
,
Вектор 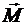 момента присоединенной пары сил направлен перпендикулярно плоскости пары
момента присоединенной пары сил направлен перпендикулярно плоскости пары  , совпадающей с плоскостью треугольника ОАВ, в ту сторону, с которой пара
, совпадающей с плоскостью треугольника ОАВ, в ту сторону, с которой пара  представляется стремящейся вращать эту плоскость в сторону, противоположную вращению часовой стрелки. Приложив его как свободный вектор в центре приведения О, убедимся, что направление совпадает с направлением вектора
представляется стремящейся вращать эту плоскость в сторону, противоположную вращению часовой стрелки. Приложив его как свободный вектор в центре приведения О, убедимся, что направление совпадает с направлением вектора  момента силы
момента силы  относительно центра приведения. Так как эти векторы равны по модулю и совпадают по направлению, то они геометрически равны, т. е.
относительно центра приведения. Так как эти векторы равны по модулю и совпадают по направлению, то они геометрически равны, т. е.
 .
.
Таким образом, силу  , не изменяя ее действия на твердое тело, можно перенести из точки ее приложения А в любой центр приведения О, приложив при этом к телу пару сил с моментом
, не изменяя ее действия на твердое тело, можно перенести из точки ее приложения А в любой центр приведения О, приложив при этом к телу пару сил с моментом 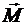 , геометрически равным моменту
, геометрически равным моменту  этой силы относительно центра приведения(рис. 4.1, в).
этой силы относительно центра приведения(рис. 4.1, в).
Этот метод был предложен французским ученым Пуансо (1777 -1859) и называется приведением силы к заданному центру.
Приведение произвольной системы сил к
Заданному центру
Применяя метод Пуансо, приведем систему трех произвольно расположенных сил  , приложенных к твердому телу в точках А1,А2 и А3 к заданному центру О. Получим три силы
, приложенных к твердому телу в точках А1,А2 и А3 к заданному центру О. Получим три силы  , приложенные в центре О, и три присоединенные пары сил
, приложенные в центре О, и три присоединенные пары сил  (рис. 4.2). Складывая силы
(рис. 4.2). Складывая силы

Рис. 4.2
 по правилу многоугольника, получим их равнодействующую
по правилу многоугольника, получим их равнодействующую  , равную геометрической сумме заданных сил и приложенную в центре приведения О:
, равную геометрической сумме заданных сил и приложенную в центре приведения О:
 .
.
Геометрическая сумма всех сил системы называется главным вектором системы сил и в отличие от равнодействующей  обозначается
обозначается  .
.
Складывая пары  , получим эквивалентную им пару сил. Момент каждой присоединенной пары сил равен моменту соответствующей силы относительно центра приведения:
, получим эквивалентную им пару сил. Момент каждой присоединенной пары сил равен моменту соответствующей силы относительно центра приведения:
 .
.
Момент пары сил, эквивалентной трем присоединенным парам сил, равен геометрической сумме моментов этих пар. Строя многоугольник моментов присоединенных пар, находим
 ,
,
т. е. момент пары сил, эквивалентной трем присоединенным парам, равен главному моменту этих трех сил относительно центра приведения. Распространяя полученные результаты на любое число сил, произвольно расположенных в пространстве, имеем
 ,
,
Этот результат можно сформулировать следующим образом: силы, произвольно расположенные в пространстве, можно привести к одной силе, равной их главному вектору и приложенной в центре приведения, и к паре сил с моментом, равным главному моменту всех сил относительно центра приведения.
Выбор центра приведения не отражается на модуле и направлении главного вектора  , но влияет на модуль и направление главного момента
, но влияет на модуль и направление главного момента  .
.
