Кафедра «Техническая механика»

Кандидат военных наук, доцент

ШАБАЕВ В.Н.

ТЕОРЕТИЧЕСКАЯ МЕХАНИКА

Курс лекций по статике и кинематике

Учебное пособие

Санкт-Петербург

Раздел 1 Статика

Лекция 1

ПРЕДМЕТ СТАТИКИ

ОСНОВНЫЕ ПОНЯТИЯ И АКСИОМЫ СТАТИКИ

Приступая к изучению статики, следует определить основные понятия, встречающиеся в этом разделе.

Материальной точкой называют материальное тело, размеры которого в рассматриваемых конкретных условиях можно не учитывать. Материальная точка обладает массой и способностью взаимодействовать с другими телами. Например, автомобиль можно считать материальной точкой при изучении его движения по дороге.

Системой материальных точек (механической системой) называют такую совокупность материальных точек, в которой положение и движение каждой точки зависят от положения и движения других точек этой системы.

Абсолютно твердым теломназывается тело, в котором расстояния между любыми его точками остаются неизменными. Реальные тела обычно могут изменять свою форму, при этом изменяются и расстояния между отдельными точками тел. Однако, в ряде случаев эти изменения (деформации) настолько малы, что ими можно пренебречь. Это значительно упрощает изучение действия сил на тело и условий, при которых эти силы уравновешиваются.

Важнейшим понятием в теоретической механике является понятие силы. Сила- это мера механического взаимодействия тел, определяющая интенсивность и направление этого взаимодействия.

Сила определяется тремя элементами: числовым значением (модулем), направлением и точкой приложения. Сила изображается вектором (рис. 1.1).

Рис. 1.1

Прямая, по которой направлена сила, называется линией действия силы. За единицу силы в Международной системе единиц - СИ принимается ньютон (Н).

Системой сил называют совокупность нескольких сил, действующих на данное тело. Системы сил, под действием каждой из которых твердое тело находится в одинаковом кинематическом состоянии, называются эквивалентными.

Сила, эквивалентная некоторой системе сил, называется равнодействующей.

Сила, равная по модулю равнодействующей и направленная по линии ее действия в противоположную сторону, называется уравновешивающей.

Приложенная система сил к твердому телу, находящемуся в покое, не выводит его из этого состояния, называется системой взаимно уравновешивающихся сил.

Силы, действующие на механическую систему, делятся на две группы: внешние и внутренние.

Внешними называются силы, действующие на материальные точки (тела) данной системы со стороны материальных точек (тел), не принадлежащих этой системе.

Внутренниминазываются силы взаимодействия между материальными точками (телами), рассматриваемой системы.

Аксиомы статики

1. Аксиома инерции. Под действием взаимно уравновешивающихся сил материальная точка (тело) находится в состоянии покоя или движется прямолинейно и равномерно.Аксиома инерции выражает установленный Галилеем закон инерции.

2. Аксиома равновесия двух сил. Две силы, приложенные к твердому телу, взаимно уравновешиваются только в том случае, если их модули равны и если они направлены по одной прямой в противоположные стороны(рис. 1.2).

Рис. 1.2 Рис. 1.3

З. Аксиома присоединения или исключения уравновешивающихся сил. Действие системы сил на твердое тело не изменится, если к ней присоединить или из нее исключить систему взаимно уравновешивающихся сил (рис. 1.3).

Следствие. Не изменяя кинематического состояния абсолютно твердого тела, силу можно переносить вдоль линии ее действия, сохраняя неизменными ее модуль и направление.

Рис. 1.4 Рис. 1.5

4. Аксиома параллелограмма сил. Равнодействующая двух пересекающихся сил приложена в точке их пересечения и изображается диагональю параллелограмма, построенного на этих силах(рис. 1.5).

Это положение выражается следующим геометрическим равенством:

.

Модуль равнодействующей силы определяется по следующей формуле:

,

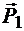где - угол между направлениями сил и .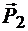

5. Аксиома равенства действия и противодействия. Всякому действию соответствует равное и противоположно направленное противодействие.

Эта аксиома утверждает, что силы действия друг на друга двух тел равны по модулю и направлены по одной прямой в противоположные стороны. Таким образом, в природе не существует одностороннего действия силы. Будучи приложенными к разным телам, эти силы не уравновешиваются. Аксиома действия и противодействия установлена Ньютоном и известна как один из основных законов классической механики.

6. Аксиома сохранения равновесия сил, приложенных к деформирующемуся телу при его затвердении.Равновесие сил, приложенныхк деформирующемуся телу, сохраняется при его затвердении.

Из этой аксиомы следует, что условия равновесия сил, приложенных к абсолютно твердому телу, должны выполняться и для сил, приложенных к деформирующемуся телу. Однако в случае деформирующегося тела эти условия необходимы, но не достаточны. Так, например, условие равновесия двух сил, приложенных к твердому телу (рис. 1. 6) на его концах, состоят в том, что силы равны по модулю и направлены по одной прямой в противоположные стороны (рис. 1.6, а, б).

Рис. 1.6

Две уравновешивающиеся силы, приложенные к нити, удовлетворяют этому условию, но при наличии добавочного условия силы должны только растягивать, а не сжимать нить (рис. 1.6, а).

Связи и их Реакции

Твердое тело, на перемещение которого не наложено никаких ограничений, называется свободным твердым телам.

Тело, ограничивающее свободу движения данного твердого тела, является по отношению к нему связью.

Твердое тело, свобода движения которого ограничена связями, называется несвободным.

Все силы, действующие на несвободное твердое тело, наряду с делением на внешние и внутренние, можно также разделить на задаваемые или активные силы и реакции связей.

Задаваемые силы выражают действие на твердое тело других тел, вызывающих или способных вызвать изменение его кинематического состояния.

Реакцией связи называется сила или система сил, выражающаямеханическое действие связи на тело.

Одним из основных положений механики является пpuнцип освобождаемости твердых тел от связей. Несвободное твердое тело можно рассматривать как свободное, на которое кроме задаваемых сил, действуют реакции связей. Пусть, например, на гладкой неподвижной горизонтальной плоскости покоится шар (рис. 1.7, а). Плоскость, ограничивая движение шара, является для него связью.

Рис. 1.7 Рис. 1.8

Если мысленно освободить шар от связи (рис. 1.7, б), то для удержания его в покое к нему в точке касания с плоскостью нужно приложить силу, равную весу шара по модулю и противоположную ему по направлению. Сила и будет реакцией плоскости. Тогда шар, освобожденный от связи, будет свободным телом, на которое действуют задаваемая сила и реакция плоскости.

Гладкая плоскость не противодействует перемещению тела вдоль плоскости под действием задаваемых сил (рис. 1.8, а), но не допускает его перемещения в направлении, перпендикулярном плоскости. Поэтому действие плоскости на тело выражается нормальной реакцией (рис. 1.8, б).

Реакция гладкой плоскости направлена перпендикулярно плоскости.

Если к концу В нити АВ, прикрепленной в точке А, подвесить груз весом (рис. 1.9, а), то реакция нити будет приложена к грузу в точке В, равна по модулю его весу и направлена вертикально вверх (рис. 1.9, б). Реакция нити направлена вдоль нити.

Пусть балка весом в точке В опирается на гладкую поверхность, а в точках А и D - на гладкие горизонтальную и вертикальную плоскости (рис. 1.10). Тогда, реакции опорной поверхности и опорных плоскостей будут иметь указанные на рис. 1.10 направления.

Рис. 1.9 Рис. 1.10

Для определения каждой реакции нужно знать три ее элемента: модуль, направление и точку приложения. Точка приложения реакции, как правило, бывает известна. Направление же реакций известно лишь для некоторых типов связей.

Если существуют два взаимно перпендикулярных направления на плоскости, в одном из которых связь препятствует перемещению тела, а в другом - нет, то направление ее реакции противоположно первому направлению.

Так, например, гладкая горизонтальная плоскость препятствует перемещению шара вертикально вниз и не препятствует его горизонтальному перемещению. В этом случае реакция плоскости направлена вверх (рис. 1.7, б). Так же определяется направление реакции нити (рис. 1.9).

Гладкая поверхность, на которую опирается балка точкой В (рис. 1.10), препятствует перемещению балки по нормали к поверхности вниз и не препятствует перемещению вдоль оси балки. Поэтому реакция этой поверхности направлена по нормали к поверхности вверх.

Аналогично, если балка опирается на ребро в точке D (точечная опора), то реакция в точке D направлена перпендикулярно оси балки (рис. 1.11).

Рис. 1.11 Рис. 1.12

Рассмотрим два основных типа опор балок и их реакции.

На рис. 1.12 изображена шарнирно-неподвижная опора, которая препятствует любому поступательному движению балки, но дает ей возможность свободно поворачиваться вокруг оси шарнира. По своей конструкции такая шарнирная опора состоит из двух обойм, из которых одна закреплена на балке, а другая - на неподвижной поверхности. Эти обоймы соединяются с помощью цилиндрического валика (на рис. 1.12 показано среднее сечение конструкции). В зависимости от действующих сил валик может прижиматься к различным точкам обоймы. Реакция шарнирно-неподвижной опоры проходит через центр шарнира О и точку соприкосновения А (рис. 1.13, а,б), но ее модуль и направление не известны.

Шарнирно-подвижная опора, нижняя обойма которой поставлена на катки, не препятствует перемещению балки параллельно опорной плоскости (рис. 1.14). Если не учитывать трения катков, то линию действия реакции такой опоры следует считать проходящей через центр шарнира перпендикулярно опорной плоскости. Таким образом, не известен лишь модуль этой реакции.

Рис. 1.13 Рис. 1.14

Шаровой шарнир (рис. 1.15) представляет собой шар, который может вращаться как угодно внутри сферической полости. Центр шара остается неподвижной точкой, через которую проходит линия действия реакции .

Подпятник (рис. 1.16) представляет собой совокупность цилиндрического шарнира, рассмотренного на рис. 1.12 и 1.13, и упорной плоскости. Подпятник закрепляет одну из точек твердого тела так, что она не может совершать никаких перемещений в пространстве. Линия действия реакции подпятника проходит через эту точку.

Рис. 1.15 Рис. 1.16

Модули реакций шарового шарнира и подпятника и их направления в пространстве неизвестны.

Пусть стержень АВ, весом которого пренебрегаем, растягивается двумя равными по модулю силами и приложенными к его концам (рис. 1.17). Рассечем мысленно стержень, разделив его нa две произвольные части AD и DB. На часть AD действуют две уравновешивающиеся силы: внешняя сила и внутреннее усилие, заменяющее действие отброшенной части стержня. Из второй аксиомы следует, что внутреннее усилие направлено по оси стержня и равно по модулю силе. Внутреннее усилие, выражающее действие отброшенной части DB на рассматриваемую АD, является по отношению к рассматриваемой части стержня внешней силой. Аналогично, на часть DB кроме силы действует внутреннее усилие , заменяющее действие части AD.

Рис. 1.17 Рис. 1.18

Если стержень АВ растягивается (рис. 1.18, а) или сжимается (рис. 1.18, б) силам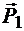и и 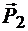, то на тела, вызывающие его растяжение или сжатие, со стороны стержня действуют реакция и . При этом реакции растянутого стержня равны по модулю задаваемым силам и направлены по оси стержня от его концов внутрь стержня.

Реакции сжатого стержня равны по модулю задаваемым силам и направлены по оси стержня к его концам. Tак как реакции и внутренние усилия по модулю равны, то для определения усилия в стержне достаточно определить его реакцию.

Таблица 1.1

Реакции связей

Наименование связей	Условные обозначения и реакции	Примечание
Опирание		Реакция связи направлена вдоль общей нормали к соприкасающимся поверхностям
Гибкие связи		Реакция направлена по касательной к гибкой связи в точку подвеса
Сферический шарнир		Направление реакции зависит от действия других (активных) сил, при решении задач принято показывать три составляющие реакции
Нагруженный стержень		Реакция направлена вдоль стержня и проходит через центры шарниров, ограничивающих стержень
Шарнирно- подвижная		Реакция направлена по нормали к поверхности качения. В стержневой аналогии этот вид связи изображается в виде одного нагруженного стержня
Шарнирно- неподвижная		Направление реакции зависит от действия других (активных) сил, при решении задач принято показывать две составляющие реакции. В стержневой аналогии связь изображается в виде двух нагруженных стержней
Жесткая заделка		Кроме составляющих реакций связи показывают пару сил с моментом М, который в этом случае называется реактивным

СистемЫ сил

Системы сил могут быть плоскими или пространственными (рис. 1.19). По расположению сил плоские и пространственные системы сил бывают: сходящимися, параллельными и произвольно расположенными.

Рис. 1.19

В сходящейся системе сил линии действия всех сил пересекаются в одной точке (рис. 1.20).

Рис. 1.20 Рис. 1.21

В параллельной системе сил линии действия сил параллельны (рис. 1.21).

В произвольно расположенной системе сил не все силы, сходящиеся или параллельные (рис. 1.22). На рис. 1.22 силы и параллельны, а сила наклонена под углом .

Рис. 1.22

Силы, приложенные к телу в какой-нибудь одной его точке (рис. 1.21, 1.22). называются сосредоточенными.

Силы, действующие на все точки данного тела или данной части тела, называются распределенными.

Распределенная нагрузка характеризуется интенсивностью q, то есть нагрузкой, приходящейся на единицу длины нагруженного отрезка, измеряется интенсивность в н/м. Равнодействующая распределенной нагрузки численно равна площади графика, занимаемого нагрузкой на чертеже и приложена к балке, проходящей через цент тяжести графика.

1. Силы, равномерно распределенные вдоль нагруженного отрезка прямой (рис. 1.23, а). Для такой системы сил интенсивность q имеет постоянное значение. При статических расчетах эту систему сил можно заменить равнодействующей , численно равной площади прямоугольника, высота которого q, а основание l.

; .

Приложена в точке С, проходящей через центр тяжести прямоугольника, т.е. делит основание АВ пополам.

2. Силы, распределенные вдоль отрезка прямой по линейному закону (рис. 1.23, б). Равнодействующая численно равна площади треугольника АВС

;

Рис. 1.23

и приложена на расстоянии от максимального значения q.

Рис. 1.24

3. Силы, распределенные вдоль отрезка прямой в виде трапеции (рис. 1.24). Равнодействующая численно равна

.

Лекция 2

СИСТЕМА СХОДЯЩИХСЯ СИЛ