Общие свойства функции распределения

Сформулируем общие свойства функции распределения:

1. 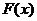- неубывающая, т.е. при , ;

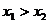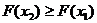2. ;

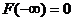3. .

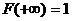Проиллюстрируем эти свойства с помощью геометрической интерпретации. Будем рассматривать случайную величину как случайную точку на оси ОХ.

Тогда 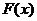есть вероятность того, что случайная точка в результате опыта попадет левее точки .

Очевидно, при этом вероятность того, что попадет левее , не может уменьшаться; следовательно, 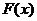с возрастанием убывать не может.

Неограниченно перемещаем точку влево по оси абсцисс. При этом попадание случайной точки левее в пределе становится невозможным событием: естественно полагать, что вероятность этого события ® 0, т.е. .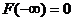

Аналогично перемещая точку вправо, убеждаемся, что 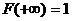, т. к. событие 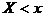становится в пределе достоверным.

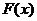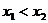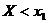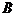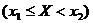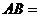То, что – монотонно неубывающая функция на всей числовой прямой, можно показать следующим образом: пусть . Рассмотрим событие = и = . Æ, 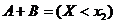. Применим теорему сложения для несовместных событий и :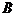

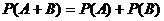
или 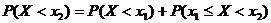, т.е. 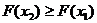, т.к. .

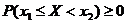Из полученного только что равенства имеем:

.

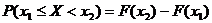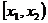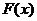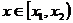Отсюда следует, что какой бы ни был задан полуинтервал , зная , мы можем рассчитывать вероятность, с которой случайная величина принимает значение . Если вероятность оказалась, например, равной нулю, то это значит, что на данном промежутке нет возможных значений .

Построим график функции распределения 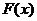– это график неубывающей функции, значения которой начинаются от 0 и доходят до 1, причем в отдельных точках функция может иметь разрывы.

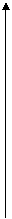F(X)

1

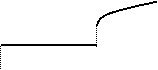
0 X

Зная ряд распределения случайной величины легко построить функцию распределения этой величины. Действительно,

,

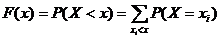где неравенство 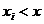под знаком суммы указывает, что суммирование распространяется на все те значения 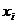, которые меньше .

Пример. Производится четыре независимых опыта, в каждом из которых может появиться или не появиться событие . Построить функцию распределения числа появлений события .

Решение. Обозначим через - число появлений события в четырех опытах. Эта величина имеет ряд распределения

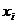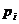	0.2401	0.4116	0.2646	0.0756	0.0081

Построим функцию распределения случайной величины

1. при 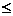0 =0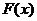

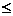2. при 0< 1 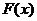=0,2401

3. при 1< 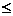2 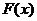=0,6517

4. при 2< 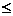3 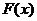=0,9163

5.при 3< 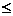4 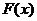=0,991

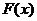6. при 4> =1

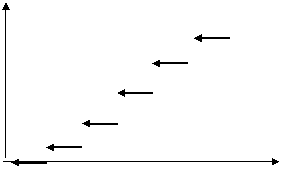0 1 2 3 4

Функция распределения любой дискретной величины есть разрывная ступенчатая функция, разрывы которой происходят в точках, соответствующих возможным значениям случайной величины.

По мере увеличения числа возможных значений случайной величины и уменьшения интервалов между ними число разрывов становится больше, а сами разрывы (скачки) меньше; ступенчатая кривая становится более плавной; случайная величина приближается к непрерывной случайной величине, а ее функция распределения - к непрерывной функции.

На практике обычно функция распределения для непрерывной случайной величины представляет собой функцию, непрерывную во всех точках.

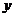
1 ----------------------

0

Плотность распределения

Пусть имеется непрерывная случайная величина с функцией распределения 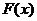, которую мы предположим непрерывной и дифференцируемой. Вычислим вероятность попадания этой случайной величины на участок от до .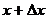

,

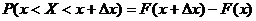т.е. приращение функции распределения на этом участке. Рассмотрим отношение этой вероятности к длине участка, т.е. среднюю вероятность, приходящуюся на единицу длины на этом участке, и будем приближать Dx®0. В пределе получим производную от функции распределения

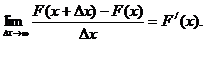
Обозначим . (*)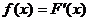

Функция 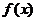- производная функции распределения, характеризует как бы плотность, с которой распределяются значения случайной величины в данной точке. Эта функция называется плотностью распределения (плотностью вероятности) непрерывной случайной величины . Иногда 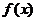называют дифференциальной функцией распределения или дифференциальным законом распределения величины .

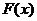
Плотность распределения так же, как и функция распределения есть одна из форм закона распределения. В противоположность функции распределения эта форма не является универсальной: она существует только для непрерывных случайных величин.

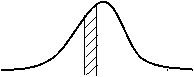
Рассмотрим непрерывную случайную величину с плотностью распределения 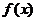и элементарный участок 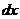, примыкающий к точке . Вероятность попадания случайной величины на этот элементарный участок есть .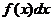

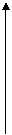
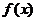
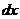
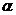Выразим вероятность попадания величины на отрезок от до 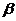через плотность распределения. Очевидно, оно равно

.

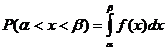Формула (*) выражает плотность распределения через функцию распределения. Зададимся обратной задачей: выразить функцию распределения через плотность. По определению

,

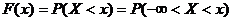откуда 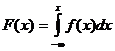.