Следствия из теоремы умножения вероятностей

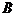Следствие 1. Если событие не зависит от события , то и событие 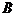не зависит от события .

Доказательство. Дано, что не зависит от 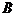, т.е. (**)

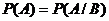Требуется доказать, что и событие 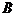не зависит от события , т. е. (**)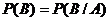

При доказательстве предполагаем, что 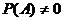. Напишем теорему вероятностей в двух формах:

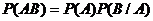
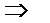
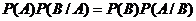
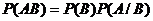
или принимая во внимание выше 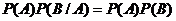. Разделим обе части на 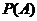. Тогда .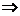

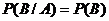Из этого следствия вытекает, что зависимость и независимость событий всегда взаимны.

Дадим другое определение.

Два события называются независимыми, если появление одного из них не изменяет вероятности появления другого. Понятие независимости событий может быть распространено на случай произвольного числа событий. Несколько событий называются независимыми, если любое из них не зависит от любой совокупности остальных.

Следствие 2. Вероятность произведения двух независимых событий равна произведению вероятностей этих событий. Это следствие непосредственно вытекает из определения независимых событий.

Теорема умножения вероятностей может быть обобщена на случай произвольного числа событий. В общем виде она формулируется так:

Вероятность произведения нескольких событий равна произведению вероятностей этих событий, причем вероятность каждого следующего по порядку события вычисляется при условии, что все предыдущие имели место:

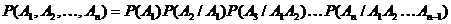
Доказательство проводится методом полной индукции. В случае независимых событий теорема упрощается и принимает вид:

,

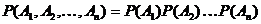т. е. вероятность произведения независимых событий равна произведению вероятностей этих событий или

.

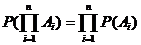Пример 1. В урне 2 белых и 3 черных шара. Из урны вынимают подряд два шара. Какова вероятность того, что оба шара белые.

- появление двух белых шаров, 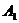- белый шар при первом вынимании, 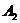- белый шар при втором вынимании; .

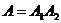По теореме .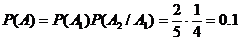

Пример 2. Те же условия, но после первого вынимания шар возвращается в урну, и шары в урне перемешиваются.

Тогда .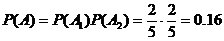

Формула полной вероятности

Следствием обеих теорем - теоремы сложения и умножения - является так называемая формула полной вероятности.

Пусть требуется определить вероятность некоторого события , которое может произойти вместе с одним из событий 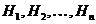, образующих полную группу несовместных событий. Будем называть эти события гипотезами.

Докажем, что в этом случае

, (*)

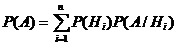т. е. вероятность события вычисляется как сумма произведений вероятности любой гипотезы на вероятность события при этой гипотезе.

Формула (*) носит название формулы полной вероятности.

Доказательство. Так как гипотезы 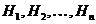образуют полную группу событий, то событие может появиться только в комбинации с какой-либо из этих гипотез

.

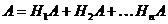Т. к. гипотезы 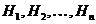несовместны, то и комбинации 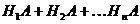- также несовместны. Покажем это - 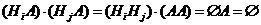. Применяя к ним теорему сложения, получим

.

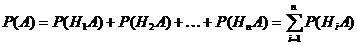Применяя к событию 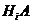теорему умножения, получим

,

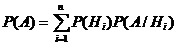что и требовалось доказать.

Пример. На фабрике, изготовляющей болты, первая машина производит 30% , вторая- 25% , третья- 45% всех изделий. Брак в их продукции составляет соответственно 2% , 1% и 3% . Найти вероятность того, что случайно выбранный болт оказался дефектным.

Решение. Обозначим через событие, состоящее в том, что случайно выбранный болт – дефектный, а через 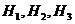– события, состоящие в том, что этот болт произведен соответственно 1-ой, 2-ой и 3-ей машинами. Из условия задачи следует, что , , ; , , .

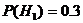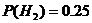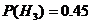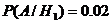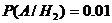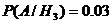По формуле полной вероятности получаем, что 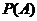=0.3·0.02+0.25·0.01+0.45·0.3=0.022.