Контрольные задачи к главе 5
«Предельные теоремы теории вероятностей»
5.1. Среднее потребление электроэнергии в мае в некотором населенном пункте составляет 360 000 кВт.ч. Оцените с помощью первого неравенства Чебышева вероятность того, что потребление электроэнергии в мае текущего года в этом населенном пункте превысит 106 кВт.ч.
5.2. Средний ежедневный расход воды в некотором населенном пункте составляет 50 000 л. Оценить с помощью первого Чебышева вероятность того, что в произвольно выбранный день расход воды в этом пункте превысит 150 000 л.
5.3. Среднее квадратическое отклонение погрешности изменения курса самолета равно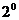 
. Считая математическое ожидание погрешности измерения равным нулю, оцените с помощью второго неравенства Чебышева вероятность того, что погрешность одного измерения курса самолета превысит 
.
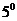5.4. Вероятность появления события A в одном опыте равна 0,5. Можно ли с вероятностью, большей 0,97, утверждать, что число появлений события A в 1000 независимых опытов будет в пределах от 400 до 600?
5.5. Средний расход воды в населенном пункте составляет 50000 литров в день. Оценить вероятность того, что в этом населенном пункте в данный день расход воды не превысит 150000 литров.
5.6. Вероятность наступления события A в каждом испытании равна 2/3. Используя неравенство Чебышева, оценить вероятность того, что в 10000 испытаний отклонение относительной частоты события A от вероятности его появлений не превзойдет 0,01.
5.7. Вопрос#19: Среднее квадратическое изменение курса акции компании в течение одних биржевых торгов составляет 0,3%. Оценить вероятность того, что на ближайших торгах курс изменится более чем на 3%.
5.8. Отделение банка обслуживает в среднем 100 клиентов в день. Оценить вероятность того, что сегодня в отделении банка будет обслужено не более 200 клиентов.
5.9. Электростанция обслуживает сеть на 1600 электроламп, вероятность включения каждой из которых равна 0,9. Оценить с помощью неравенства Чебышева вероятность того, что число ламп, включенных в сеть вечером, отличается от своего математического ожидания не более чем на 100 (по абсолютной величине).
5.10. Вероятность того, что акции, переданные на депозит, будут востребованы, равна 0,08. Оценить с помощью неравенства Чебышева вероятность того, что среди 1000 клиентов от 70 до 90 востребуют свои акции.
5.11. Среднее значение длины детали 50 см, а дисперсия – 0,1. Оценить с помощью неравенства Чебышева вероятность того, что случайно взятая деталь окажется по длине не менее 49,5 см и не более 50,5 см. Уточнить вероятность того же события, если известно, что длина случайно взятой детали имеет нормальный закон распределения.
5.12. В течение времени t эксплуатируются 500 приборов. Каждый прибор имеет надежность 0,98 и выходит из строя независимо от других. Оценить с помощью неравенства Чебышева вероятность того, что доля надежных приборов отличается от 0,98 не более чем на 0,1 (по абсолютной величине).
5.13. Вероятность сдачи в срок всех экзаменов студентом факультета равна 0,7. Оценить с помощью неравенства Чебышева вероятность того, что доля сдавших в срок все экзамены из 2000 студентов заключена в границах от 0,66 до 0,74.
5.14. В среднем 10% работоспособного населения некоторого региона – безработная. Оценить с помощью неравенства Чебышева вероятность того, что уровень безработицы среди обследованных 10000 работоспособных жителей города будет в пределах от 9 до 11% включительно.
5.15. Сколько нужно провести измерений, чтобы с вероятностью, равной 0,9973, утверждать, что погрешность средней арифметической результатов этих измерений не превысит 0,01, если измерение характеризуется средним квадратическим отклонением, равным 0,03?
5.16. Случайная величина Х является средним арифметическим из n независимых одинаково распределенных случайных величин, дисперсия каждой из которых равна 5. Оцените, какое число слагаемых n нужно взять для того, чтобы с вероятностью не менее 0,9973 случайная величина Х отклонялась от своего среднего не более чем на 0,01.
5.17. Среднее квадратическое отклонение погрешности изменения курса самолета равно 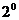. Считая математическое ожидание погрешности измерения равным нулю, оцените с помощью второго неравенства Чебышева вероятность того, что погрешность одного измерения курса самолета превысит .
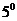5.18. Случайная величина Х является средним арифметическим из 3200 независимых случайных величин, причем каждое слагаемое имеет математическое ожидание 3 и дисперсию 2. Оценим вероятность того, что Х попадает в интервал (2,925, 3,075).
5.19. Производится выборочное обследование большой партии электрических лампочек. Среднее квадратическое отклонение времени горения лампочки равно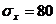 
ч. Из всей партии наудачу выбирается 400 лампочек. Оценить вероятность того, что среднее время горения лампочки будет отличаться от наблюдаемого среднего времени горения выбранных 400 лампочек не более чем на 10 ч.
5.20. Три станка, производительности которых соотносятся как 3:2:1,производят детали на общий конвейер. Определить вероятность того, что из 200 деталей, взятых случайным образом с конвейера, деталей, произведенных вторым станком будет от 50 до 70.
5.21. 3 станка производят детали из стали марки A , 7 других – из стали марки B. Определить вероятность того, что из 400 взятых деталей количество деталей из стали марки A будет заключено в пределах от 100 до 130.
5.22. Отделение банка обслуживает в среднем 100 клиентов в день. Оценить вероятность того, что сегодня в отделении банка будет обслужено более 150 клиентов.
5.23. Три станка, производительности которых соотносятся как 5:3:2, производят детали на общий конвейер. Определить вероятность того, что из 200 деталей, взятых случайным образом с конвейера, деталей, произведенных вторым станком будет от 50 до 65.
5.24. Найти вероятность того, что при 720 бросаниях игральной кости «шестерка» выпадает от 100 до 130 раз.
5.25. Вероятность появления некоторого события в каждом из 800 независимых испытаний равна 1/4. Воспользовавшись вторым неравенством Чебышева, оцените вероятность того, что число Х появлений этого события заключено в пределах от 150 до 250.