Основные этапы математического и инфологического моделирования

1. Постановка задачи.

1.1. Формулировка.

1.2. Определение цели моделирования и их приоритетов.

1.3. Сбор информации о системе, объекте моделирования.

1.4. Описание данных (их структуры, диапазон источника и т. д.).

2. Предмодельный анализ.

2.1. Анализ существующих аналогов и подсистем.

2.2. Анализ технических средств моделирования (ЭВМ и др.).

2.3. Анализ программного обеспечения (языки программирования, инструментальные среды, пакеты программ)

2.4. Анализ математического обеспечения (модели, методы, алгоритмы).

3. Анализ задачи (модели).

3.1. Разработка структур данных.

3.2. Разработка входных и выходных спецификаций, форм и представлений данных.

3.3. Проектирование структуры и состава модели (подмодели).

4. Исследование модели.

4.1. Выбор методов исследования подмодели.

4.2. Выбор, адаптация или разработка алгоритма.

4.3. Сборка модели в целом из подмоделей.

4.4. Идентификация модели если в этом есть необходимость.

4.5. Формулировка используемых критериев адекватности моделируемой системы устойчивости и чувствительности.

5. Программирование (проектирование программы).

5.1. Выбор метода тестирования и теста (контрольные примеры).

5.2. Кодирование на языке программирования.

5.3 Комментирование программы.

6. Тестирование и отладка.

6.1. Синтаксическая отладка.

6.2. Семантическая отладка (отладка логической структуры).

6.3 Тестовые расчёты, анализ результатов тестирования.

6.4. Оптимизация программы.

7. Оценка моделирования.

7.1. Оценка средств моделирования.

7.2. Оценка адекватности моделируемой системы.

7.3. Оценка чувствительности модели.

7.4. оценка устойчивости модели.

8. Документирование.

8.1. Описание задач и цели.

8.2. Описание метода, алгоритма.

8.3 Описание среды реализации.

8.4. Описание возможностей и ограничений.

8.5. Описаний входных и выходных форматов, спецификаций.

8.6. Описание тестирования.

8.7.Описание инструкции пользователя.

9. Сопровождение.

9.1. Анализ использования, периодичность использования возможность количества пользователей, анализ отказов.

9.2. Обслуживание модели алгоритма программы и их эксплуатация.

9.3. Расширение возможностей: включение новых функций или изменение режимов моделирования.

9.4. Нахождение , исправление скрытых ошибок в программе, если они найдутся.

10. Использование модели.

Решение краевых задач.

Опр. Краевой задачей называется задача, в которой определённым образом задано условие на краях исследуемой области. Условия определяют поведение искомой функции.

Опр. ( постановка краевых задач).

Решить дифференциальное уравнение y"=f(x,y,y'), при чём обязательно заданы граничные условия. Найти значения y в каждой точке фиксированной x.

Краевые задачи делятся на разные виды в зависимости от начальных условий:

1. Если граничные условия имеют вид: y(a)=A, y(b)=B. Где А и В либо константы, либо функция, то это краевые условия первого рода.

2. Если граничные условия имеют вид: y'(a)=A, y'(b)=B, то это краевая задача второго рода.

3. Если известны комбинации: α₁·y'(a)+β₁·y(a)=γ₁ и

α₂·y'(a)+β₂·y(a)=γ₂ то это краевая задача третьего рода.

Для задач первого рода известна функция, т.е. например, известно значение температуры на краях стержня.

Для задач второго рода на границах сама функция неизвестна, а известна её производная.

Для задач третьего рода неизвестно значение функции, неизвестна производная, а известна их комбинация.

Краевые задачи делятся на три основных типа:

1. Параболического типа (пример: уравнения теплопроводности).

2. Гиперболического типа (уравнение описывающее колебание струны).

3. Эллиптического типа.

Рассмотрим краевую задачу 2-го рода параболического типа.

Задача: (моделирует процессы теплопереноса).

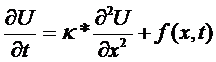
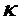- коэффициент.

f – функция внутренних тепловых источников.

U – температура.

Начальные условия:

U(x,0)=φ(x)

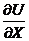_x=a = f(t) - левое граничное условие

U(b)=q(t) - правое граничное условие

Для её решения использую метод сеток.

Решение:

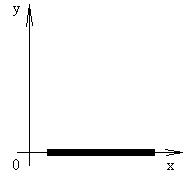Изобразим декартовую систему координат, где отложим х (точка стержня) и у (момент времени).

Рассмотрим стержень.

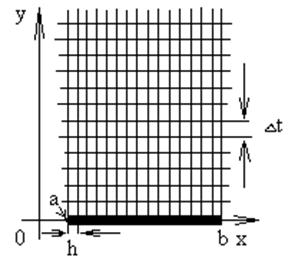Разобьем участок стержня на n равных частей и рассмотрим шаг h=(b-a)/n (см. рисунок).

Для выбора шага по времени используем условие устойчивости: 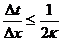это условие применяется для явной сетки, когда последующий слой считается через предыдущий. Если это условие будет не соблюдаться, то в программе могут возникать неадекватные результаты: очень большие числа или числа разных знаков. Обычно 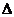t приходится выбирать очень маленьким, например 0,001, 0,0001, что затрудняет процесс счёта на компьютере. Например реальный процесс, который происходит 2 секунды моделируется на компьютере 2 часа.

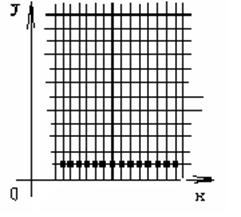
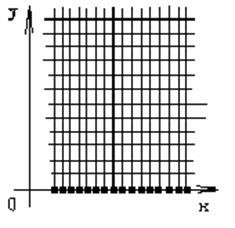Используя условие U(x,0)=φ(x) мы можем найти значение температуры в каждой точке стержня в начальный момент времени, т.е. посчитать значение в следующих узлах сетки:

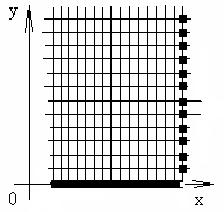Используя, правое граничное условие, мы найдём значение температуры на правом краю стержня во все моменты времени. На сетке эти точки будут расположены следующим образом:

(см. рисунок).

Затем, используя основное уравнение теплопроводности и выразив последующий слой через предыдущий мы можем найти значения температуры в следующих точках (см. рисунок).

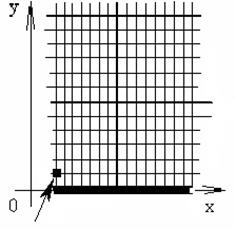И наконец распишем производную на левой границе: 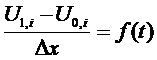Найдём значение в точке U_0,I:

U_0,i= U_1,i-

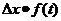
Значение в данной точке будет соответствовать следующему узлу сетки (см рисунок).

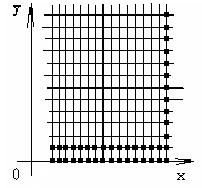Таким образом мы посчитаем значения температуры в следующих узлах (см. рисунок)

Таким образом мы можем посчитать температуру во всей сетке (во всех узлах) и будем знать температуру стержня в каждой точке стержня в каждый момент времени.(Для получения более подробных сведений обращаётесь в раздел численных методов – решение краевых задач.)

Алгоритм программы.

В программе можно использовать два одномерных массива, либо один двумерный массив.

Одномерный массив описывается следующим образом:

U0[0..n] – используется для хранения данных предыдущего слоя,

U1[0..n] – используется для хранения данных последующего слоя.

Задаём начальные условия в цикле, т.е. для каждой точки стержня задаём значение температуры в нулевой момент времени:

For i:=0 to nx do { n - количество разбиений стержня}

Begin

U0[i]=φ(x) {в качестве φ(x) ,берётся функция из граничного условия}

x:=i*dx {dx –шаг, который задаётся в начале программы самостоятельно}

Затем открываем цикл по времени:

For j:=1 to T do {T – конечный момент времени}

Begin

U1[n]:=q(t1) { в качестве q(t1) ,берётся функция из правого граничного условия }

t1:=dt*j { dt –шаг, который задаётся в начале программы исходя из условия устойчивости – тоже самое что и }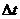

Затем решаем основное уравнение теплопроводности. Предварительно расписав его в разностном виде:

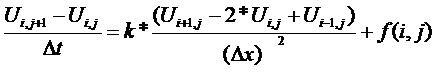
Где U_i,j+1 - это U[i]

U_i,j - это U0[i]

U_i+1,j - это U0[i+1]

U_i-1,j - это U0[i-1]

Выражаем последующий слой через предыдущий:

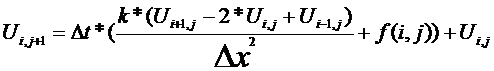
т.е. for i:=1 to n-1 do

U1[i]:=dt*(k*(U0[i+1]-2*U0[i]+U0[i-1])/(dx*dx)+f(i))+U0[i]

Т.о. мы посчитаем температуру на следующем слое , в точках соответствующих индексам от 1 до n-1.

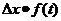Используя левое граничное условие найдём: U_0,i= U_1,i- т.е.

U1[0]:=U1[1]-dx*f(t) {где f(t) функция т левого граничного условия}

Затем выводим слой (результат) на экран:

For i:=0 to 1 do

Write(u1[i]);

Writeln;

Переприсваиваем слои:

U0:=U1 ;

Заканчиваем цикл по времени. Заканчиваем программу.