Модель теоретико-множественная

Если она представима с помощью некоторых множеств и отношений принадлежности им и между ними.

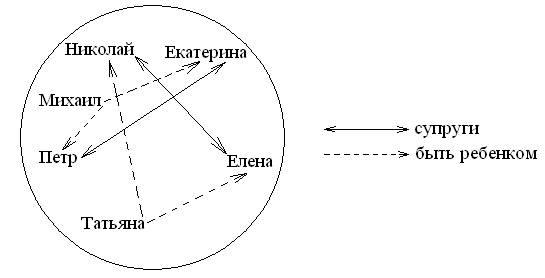
Пример: Пусть задано множество X = Николай, Петр, Николаев, Петров, Елена, Екатерина, Михаил, Татьяна. Заданы отношения: Николай – супруг Елены, Екатерина – супруга Петра, Татьяна – дочь Николая и Елены, Михаил – сын Петра и Екатерины. Семья Николая и Петра дружат друг с другом. Множество X и множество перечисленных отношений Y могут служить теоретико-множественной моделью двух дружеских семей.

Изобразить с помощью графов:

Модель логическая

Если она представима предикатами или логическими функциями.

Пример: Совокупность двух логических функций

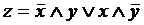
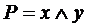
может служить математической моделью одноразрядного сумматора.

Модель игровая

Если она описывает, реализует некоторую игровую ситуацию.

Модель алгоритмическая

Если она описана некоторым алгоритмом или комплексом алгоритмов, определяющим её функции.

Пример: Алгоритмической моделью квадратного корня может служить алгоритм вычисления его приближенного сколь угодно точного отношения по известной рекуррентной формуле.

Модель языковая (лингвистическая)

Если она представлена некоторым лингвистическим объектом, формализованной языковой системой или структурой.

Пример: Правило дорожного движения.

Языковая структурная модель движения транспорта и пешеходов.

Модель визуальная

Если она позволяет визуализировать отношения и связи моделируемой системы.

Модель натурная

Если она материальная копия объекта моделирования.

Пример: Глобус.

Модель геометрическая

Если она представима геометрическими образами и объектами.

Пример: Прямая линия является моделью числовой оси.

Параллелограмм является моделью плоскости, либо моделью квадрата.

Модель клеточно-автоматная

Если она представляет систему с помощью клеточного автомата.

Пример: Классическая клеточно-автоматная модель: игра «жизнь» Дж. Конвея.

Модель фронтальная

Самая сложная, она описывает эволюцию моделируемой систему эволюции фронтальных объектов.

Пример: Множество Кантора.

Возьмем отрезок [0; 1] и разобьем его на три части.

Выбросим из донного отрезка средний отрезок и каждый из оставшихся отрезков опять разобьем на три части.

Из каждого отрезка выбросим средние части и каждый из оставшихся отрезков опять разобьем на три части.

Продолжая разбиение таким образом получим множество называемое множеством Квантора.

В пределе получаем несчетное множество изолируемых точек.

Фронтальная модель применяется обычно тогда, когда реальный объект нельзя представить в виде классической модели. Когда имеем дело с нелинейностью (много вариантностью) путей развития, необходимостью выбора и недетерминированностью (хаотичностью и необратимостью) процесса.

Пример: Математические модели динамики эпидемии инфекционной болезни, радиоактивного распада, усвоение второго иностранного языка и др..