Определение параметров уравнения регрессии

На любой экономический показатель чаще всего оказывает влияние не один, а несколько факторов. Например, спрос на некоторое благо определяется не только ценой данного блага, но и ценами на замещающие и дополняющие блага, доходом потребителей и многими другими факторами. В этом случае вместо парной регрессии 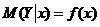рассматривается множественная регрессия

.

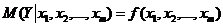(6.1)

Задача оценки статистической взаимосвязи переменных Y и 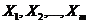формулируется аналогично случаю парной регрессии. Уравнение множественной регрессии может быть представлено в виде

,

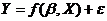(6.2)

где 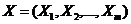— вектор независимых (объясняющих) переменных; 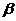— вектор параметров (подлежащих определению); 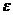— случайная ошибка (отклонение); Y — зависимая (объясняемая) переменная. Рассмотрим самую употребляемую и наиболее простую из моделей множественной регрессии — модель множественной линейной регрессии.

Теоретическое линейное уравнение регрессии имеет вид:

,

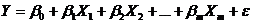(6.3)

или для индивидуальных наблюдений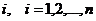

.

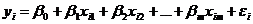(6.4)

Здесь 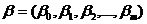— вектор размерности (т+1) неизвестных параметров.

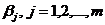называется j-м теоретическим коэффициентом регрессии (частичным коэффициентом регрессии). Он характеризует чувствительность величины 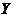к изменению 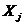, т.е. отражает влияние на условное математическое ожидание 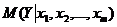зависимой переменной 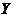объясняющей переменной 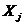при условии, что все другие объясняющие переменные модели остаются постоянными.

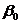— свободный член, определяющий значение 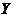в случае, когда все объясняющие переменные 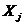, равны нулю.

После выбора линейной функции в качестве модели зависимости необходимо оценить параметры регрессии.

Пусть имеется п наблюдений вектора объясняющих переменных 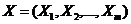и зависимой переменной : .

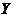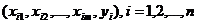Для того чтобы однозначно можно было бы решить задачу отыскания параметров 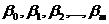, (т.е. найти некоторый наилучший вектор 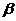), должно выполняться неравенство 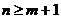. Если это неравенство не будет выполняться, то существует бесконечно много различных векторов параметров, при которых линейная формула связи между X и 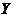будет абсолютно точно соответствовать имеющимся наблюдениям. При этом, если 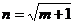, то оценки коэффициентов вектора 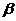рассчитываются единственным образом — путем решения системы 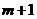линейного уравнения:

, .

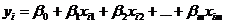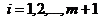(6.5)

Число 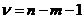называется числом степеней свободы. Если число степеней свободы невелико, то статистическая надежность оцениваемой формулы невысока. Считается, что при оценивании множественной линейной регрессии для обеспечения статистической надежности требуется, чтобы число наблюдений по крайней мере в 3 раза превосходило число оцениваемых параметров.

Самым распространенным методом оценки параметров уравнения множественной линейной регрессии является метод наименьших квадратов (МНК). Напомним, что его суть состоит в минимизации суммы квадратов отклонений наблюдаемых значений зависимой переменной 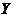от ее значений 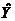, получаемых по уравнению регрессии.

Предпосылки МНК

1. Математическое ожидание случайного отклонения 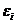, равно нулю для всех наблюдений: .

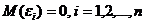2. Гомоскедастичность (постоянство дисперсии отклонений). Дисперсия случайных отклонений 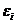постоянна: 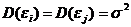для любых наблюдений 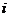и .

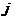3. Отсутствие автокорреляции. Случайные отклонения 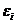и 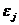являются независимыми друг от друга для всех .

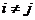4. Случайное отклонение должно быть независимо от объясняющих переменных: .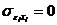

5. Модель является линейной относительно параметров.

Для случая множественной линейной регрессии существенными являются еще две предпосылки.

6. Отсутствие мультиколлинеарности. Между объясняющими переменными отсутствует строгая (сильная) линейная зависимость.

7. Ошибки 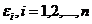, имеют нормальное распределение ( ).

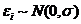Выполнимость данной предпосылки важна для проверки статистических гипотез и построения интервальных оценок.

Как и в случае парной регрессии, истинные значения параметров 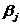по выборке получить невозможно. В этом случае вместо теоретического уравнения регрессии (6.3) оценивается так называемое эмпирическое уравнение регрессии. Эмпирическое уравнение регрессии представим в виде:

.

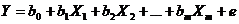(6.6)

Здесь 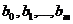— оценки теоретических значений 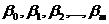коэффициентов регрессии (эмпирические коэффициенты регрессии); е — оценка отклонения 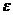. Для индивидуальных наблюдений имеем:

.

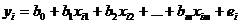(6.7)

Оцененное уравнение в первую очередь должно описывать общий тренд (направление) изменения зависимой переменной Y. При этом необходимо иметь возможность рассчитать отклонения от этого тренда.

По данным выборки объема п: 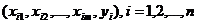, требуется оценить значения параметров 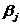вектора 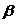, т.е. провести параметризацию выбранной модели (здесь 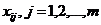значение переменной 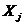в i-м наблюдении).

При выполнении предпосылок МНК относительно ошибок 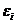оценки 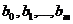параметров 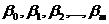множественной линейной регрессии по МНК являются несмещенными, эффективными и состоятельными.

Отклонение 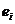значения 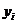зависимой переменной Y от модельного значения 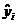соответствующего уравнению регрессии в i-м наблюдении ( 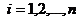), рассчитывается по формуле

.

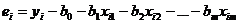(6.8)

Тогда по МНК для нахождения оценок 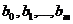минимизируется следующая функция

.

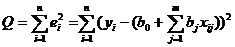(6.9)

Данная функция является квадратичной относительно неизвестных величин 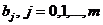. Она ограничена снизу, следовательно, имеет минимум. Необходимым условием минимума функции Q является равенство нулю всех ее частных производных по 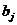. Частные производные квадратичной функции (6.9) являются линейными функциями

.

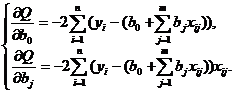(6.10)

Приравнивая их к нулю, мы получаем систему т+1 линейных уравнений с т+1 неизвестными:

.

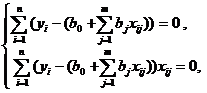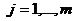(6.11)

Система (6.11) называется системой нормальных уравнений. Ее решение в явном виде наиболее наглядно представимо в векторно-матричной форме.