Неопределённый интеграл и его свойства
Неопределённый интеграл и его свойства
Первообразная и неопределённый интеграл
В дифференциальном исчислении решается задача: по данной функции 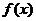 найти её производную (или дифференциал). Интегральное исчисление решает обратную задачу: найти функцию
найти её производную (или дифференциал). Интегральное исчисление решает обратную задачу: найти функцию  , зная её производную
, зная её производную 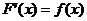 (или дифференциал). С такой задачей мы встречаемся и в экономике, например, при нахождении функции оборотных средств по известной скорости формирования оборотных средств.
(или дифференциал). С такой задачей мы встречаемся и в экономике, например, при нахождении функции оборотных средств по известной скорости формирования оборотных средств.
Функция  называется первообразнойдля функции
называется первообразнойдля функции 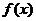 на интервале
на интервале 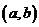 , если для любого
, если для любого 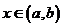 выполняется равенство
выполняется равенство
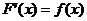 .
.
Например, первообразной функции 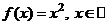 , является функция
, является функция 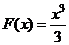 , действительно
, действительно 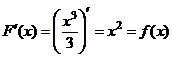 . Первообразными будут также функции
. Первообразными будут также функции 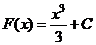 (
( 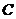 - постоянная), которые также удовлетворяют условию .
- постоянная), которые также удовлетворяют условию .
Если  первообразная для
первообразная для 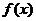 , то выражение
, то выражение 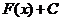 , где
, где 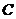 - произвольная постоянная, называется неопределённым интеграломот функции
- произвольная постоянная, называется неопределённым интеграломот функции 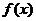 и обозначается символом
и обозначается символом 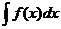 , где
, где 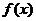 - подынтегральная функция,
- подынтегральная функция, 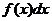 - подынтегральное выражение,
- подынтегральное выражение, 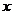 - переменная интегрирования.
- переменная интегрирования.
Таким образом,
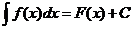 .
.
Например, 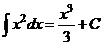 .
.
Нахождение первообразной по её производной или отыскание неопределённого интеграла по данной подынтегральной функции называется интегрированиемданной функции. Интегрирование – операция, обратная дифференцированию. Для того чтобы проверить, правильно ли выполнено интегрирование, надо взять производную от полученного результата и убедиться, что получена подынтегральная функция.
Свойства неопределённого интеграла. Таблица основных интегралов. Приёмы непосредственного интегрирования
 Производная от неопределённого интеграла равна подынтегральной функции; дифференциал от неопределённого интеграла равен подынтегральному выражению, т.е.
Производная от неопределённого интеграла равна подынтегральной функции; дифференциал от неопределённого интеграла равен подынтегральному выражению, т.е.
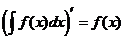 ;
; 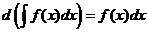 .
.
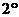 Неопределённый интеграл от дифференциала некоторой функции равен этой функции плюс произвольная постоянная, т.е.
Неопределённый интеграл от дифференциала некоторой функции равен этой функции плюс произвольная постоянная, т.е.
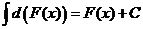 .
.
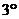 Постоянный множитель можно вынести из под знака неопределённого интеграла, т.е.
Постоянный множитель можно вынести из под знака неопределённого интеграла, т.е.
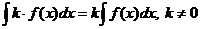 .
.
 Неопределённый интеграл от алгебраической суммы функций равен сумме интегралов от слагаемых, т.е.
Неопределённый интеграл от алгебраической суммы функций равен сумме интегралов от слагаемых, т.е.
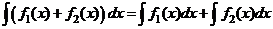 .
.
Приведём таблицу основных интегралов
I. 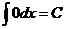 .
.
II. 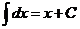 .
.
III. 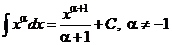 .
.
IV. 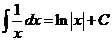 .
.
V. 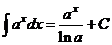 .
.
VI. 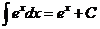 .
.
VII. 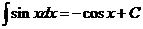 .
.
VIII. 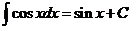 .
.
IX. 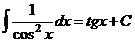 .
.
X. 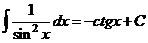 .
.
XI. 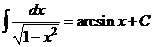 .
.
XII. 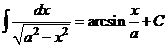 .
.
XIII. 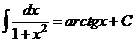 .
.
XIV. 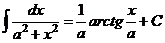 .
.
XV. 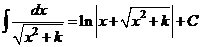 .
.
XVI. 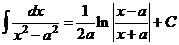 .
.
Справедливость формул проверяется дифференцированием.
Вычисление интегралов с помощью таблицы основных интегралов и простейших приёмов называется непосредственным интегрированием.
Пример 1. Найти 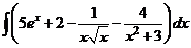 .
.
Решение
Применив свойства 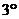 и
и  , имеем
, имеем
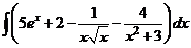 =
=
= 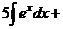
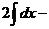
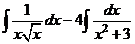 .
.
Далее находим интегралы с использованием табличных формул:
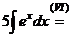
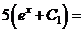
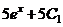 ;
;
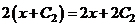 ;
;
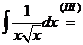
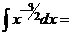
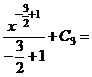
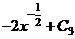 ;
;
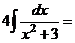
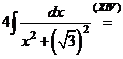
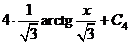 .
.
Таким образом,
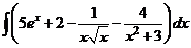 =
= 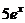 +
+ 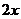 +
+ 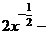
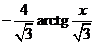 +
+ 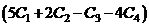 .
.
Обычно, все произвольные постоянные суммируют, результат обозначают одной буквой, поэтому
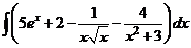 =
= 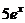 +
+ 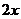 +
+ 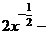
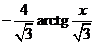 +
+ 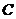 .
.
Пример 2. Найти интегралы, разложив подынтегральную функцию в сумму функций:
а) 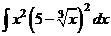 ;
;
б) 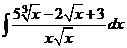 ;
;
в) 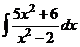 .
.
Решение
а) Применяя формулу сокращенного умножения и умножая почленно, преобразуем подынтегральную функцию в сумму:
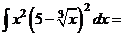
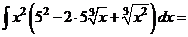
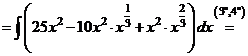
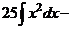
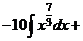
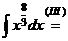
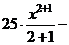
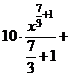
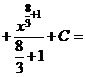
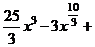
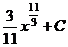 .
.
б) Разделим почленно числитель на знаменатель, применим свойства 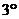 ,
,  и табличные интегралы III, IV.
и табличные интегралы III, IV.
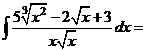
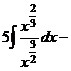
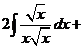
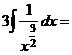
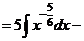
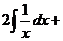
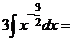
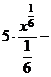
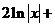
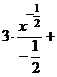
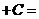
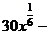
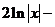
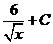 .
.
в) Для разложения подынтегральной функции в сумму функций разделим числитель на знаменатель «углом».
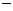 | 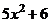 | 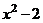 |
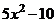 | 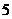 | |
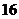 |
Следовательно, 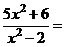
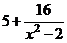 , тогда
, тогда
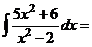
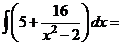
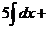
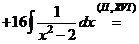
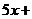
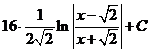 .
.
Решение
а) Чтобы избавиться от иррациональности, выполним замену переменной 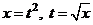 .
.
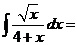
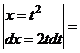
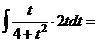
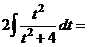
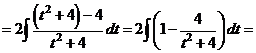
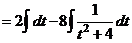
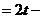
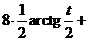
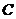 .
.
Возвращаясь к 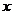 , получим
, получим
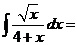
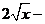
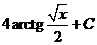 .
.
б) 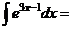
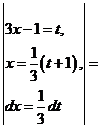
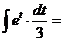
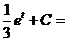
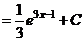 .
.
в) 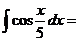
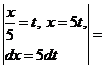
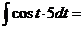
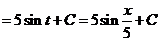 .
.
г) 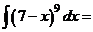
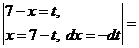
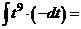
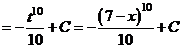 .
.
При вычислении интегралов б, в, г была использована линейная подстановка 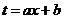 . В общем случае справедлива формула
. В общем случае справедлива формула
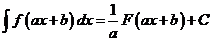 ,
,
Формулу применяют также в обратном направлении
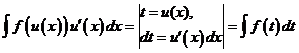 .
.
В этом случае говорят о наличии дифференциальной связи.
Пример 4. Найти интегралы, используя наличие дифференциальной связи:
а) 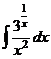 ; б)
; б) 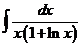 ; в)
; в) 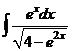 ; г)
; г) 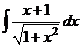 .
.
Решение
а) 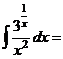
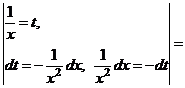
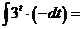
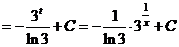 .
.
б) 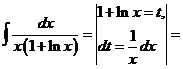
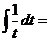
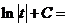
 .
.
в) 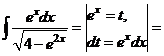
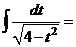
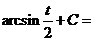
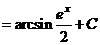 .
.
г) 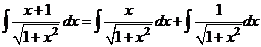 .
.
В первом из интегралов выполним замену
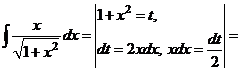
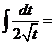
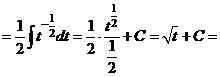
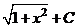 .
.
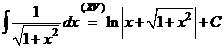 ,
,
значит
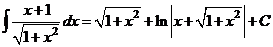 .
.
Решение
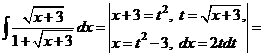
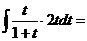
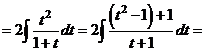
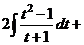
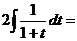
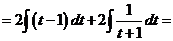
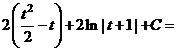
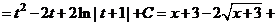
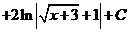 .
.
Определённый интеграл
Решение
Так как одной из первообразных для функции  является
является  , то применяя формулу , получим
, то применяя формулу , получим
 .
.
Решение




 .
.
 Интеграл от неотрицательной функции на отрезке
Интеграл от неотрицательной функции на отрезке  - неотрицательное число, то есть если
- неотрицательное число, то есть если  на
на  , то
, то  .
.
 Если на
Если на  выполняется неравенство
выполняется неравенство  , то такое же неравенство выполняется и для интегралов, т.е.
, то такое же неравенство выполняется и для интегралов, т.е.
 .
.
 Пусть
Пусть  - наименьшее, а
- наименьшее, а  - наибольшее значения непрерывной функции
- наибольшее значения непрерывной функции 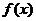 на
на  , тогда
, тогда
 .
.
Пример 11. Оценить определённый интеграл  .
.
Решение
Функция  убывает на промежутке
убывает на промежутке  , поэтому
, поэтому  ,
,  . Значит
. Значит  ,
,  .
.
 Если
Если 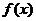 непрерывна на отрезке
непрерывна на отрезке  , то найдётся такое значение
, то найдётся такое значение  , что
, что  .
.
 - среднее значение функции
- среднее значение функции 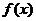 на отрезке
на отрезке  .
.
При вычислении определённых интегралов применяют также метод замены переменной, который позволяет упростить интеграл. При этом в отличие от неопределённого интеграла нет необходимости возвращаться к исходной переменной интегрирования. Достаточно найти пределы интегрирования новой переменной и воспользоваться формулой Ньютона-Лейбница.
Формула замены переменной в определённом интеграле имеет вид
 .
.
Пример 12. Вычислить интегралы:
а)  ; б)
; б)  .
.
Решение
а) 



 .
.
б) 




 .
.
Формула интегрирования по частям в определённом интеграле имеет вид
 .
.
Пример 13. Вычислить интеграл  .
.
Решение



 ,
,
так как  ,
,  .
.
Решение
Фигура заключена между графиками функций 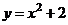 и
и 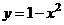 . Площадь
. Площадь 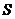 находим как разность площадей
находим как разность площадей
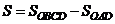 .
.
 Вычисление объёма тела вращения. Пусть
Вычисление объёма тела вращения. Пусть 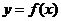 - непрерывна и неотрицательна на
- непрерывна и неотрицательна на  (рис.2). Тогда тело, образованное вращением вокруг оси
(рис.2). Тогда тело, образованное вращением вокруг оси 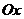 криволинейной трапеции
криволинейной трапеции 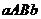 , имеет объём
, имеет объём
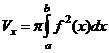 .
.
 |
Рис. 2
Пример 15. Найти объём тела (рис.3), полученного от вращения фигуры, ограниченной линиями 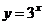 ,
, 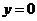 ,
, 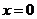 ,
, 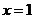 .
.
 |
Рис. 3
Решение
Искомый объём равен 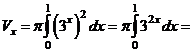
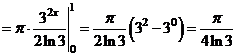 .
.
 Экономические приложения определённого интеграла
Экономические приложения определённого интеграла
Пример 16. Дана функция предельных издержек
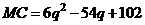 ,
, 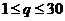 ,
,
где 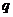 - объём выпускаемого товара. Найти функцию издержек
- объём выпускаемого товара. Найти функцию издержек
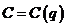
и вычислить издержки в случае производства 10 единиц товара, если известно, что издержки для производства первой единицы товара составили 30 рублей.
Решение
Известно, что предельные издержки 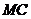 есть производная от функции издержек
есть производная от функции издержек 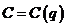 , т.е.
, т.е. 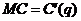 . Значит, функцию издержекнаходим интегрированием
. Значит, функцию издержекнаходим интегрированием
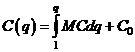 .
.
Для заданной функции 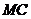 имеем
имеем
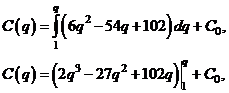
или
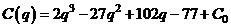 .
.
Из условия 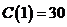 найдём
найдём 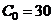 . Тогда получаем,
. Тогда получаем,
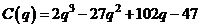 .
.
При 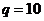 вычислим
вычислим 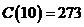 .
.
Пример 17. Функция изменения затрат времени на изготовление изделий имеет вид 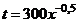 . Найти среднее время, затраченное на освоение одного изделия в период освоения от
. Найти среднее время, затраченное на освоение одного изделия в период освоения от 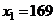 до
до 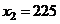 .
.
Решение
Если известна функция 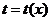 , описывающая изменение затрат времени на изготовление изделия в зависимости от степени освоения производства, где
, описывающая изменение затрат времени на изготовление изделия в зависимости от степени освоения производства, где 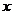 - порядковый номер изделия в партии, то среднее время, затраченное на изготовление одного изделия в период освоения от
- порядковый номер изделия в партии, то среднее время, затраченное на изготовление одного изделия в период освоения от 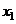 до
до 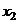 , вычисляется с помощью интеграла
, вычисляется с помощью интеграла
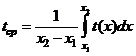 .
.
В нашем случае
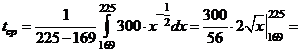
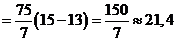 .
.
Несобственные интегралы
При определении определённого интеграла предполагалось, что отрезок интегрирования конечен, а подынтегральная функция ограничена на этом отрезке. Однако возможны случаи, когда одно или оба этих условия не выполняются. В этом случае соответствующие интегралы называются несобственными.
Пусть функция 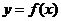 интегрируема на каждом конечном отрезке
интегрируема на каждом конечном отрезке  , т.е. существует определённый интеграл
, т.е. существует определённый интеграл 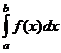 . Тогда за несобственный интеграл
. Тогда за несобственный интеграл 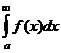 принимают предел
принимают предел
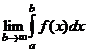 .
.
Если предел существует и конечен, то говорят, что несобственный интеграл сходится. В противном случае говорят, что расходится.
Итак,
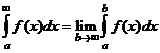 .
.
Аналогично можно рассмотреть несобственный интеграл с бесконечным нижним пределом
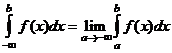 .
.
Или с бесконечными верхним и нижним пределами интегрирования 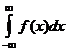 .
.
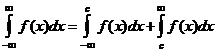 .
.
Если существуют несобственные интегралы 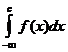 и
и 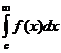 , то существует и несобственный интеграл
, то существует и несобственный интеграл 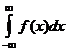 , независящий от выбора промежуточной точки
, независящий от выбора промежуточной точки 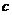 .
.
Пример 18. Найти несобственные интегралы:
а) 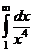 ; б)
; б) 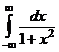 ; в)
; в) 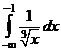 .
.
Решение
а) По определению имеем
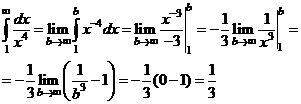
Несобственный интеграл сходится и равен 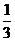 .
.
б) 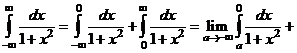
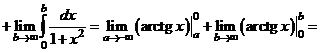
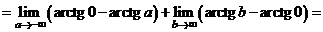
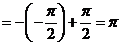 .
.
Интеграл сходится.
в) 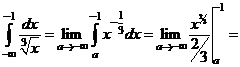
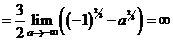 .
.
Интеграл расходится.
Кроме несобственных интегралов с бесконечными пределами интегрирования в литературе рассматриваются несобственные интегралы от неограниченных функций. Предлагаем изучить этот материал самостоятельно.
Решение
Уравнение линий уровня
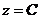 или
или 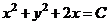 .
.
Приведём к виду 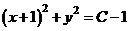 . Это уравнение окружности с центром в точке (-1; 0) и радиусом
. Это уравнение окружности с центром в точке (-1; 0) и радиусом 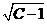 (рис.4). Линии уровня – концентрические окружности, радиус которых увеличивается с ростом
(рис.4). Линии уровня – концентрические окружности, радиус которых увеличивается с ростом 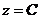 . Точка (-1; 0) – вырожденная линия уровня, соответствующая значению
. Точка (-1; 0) – вырожденная линия уровня, соответствующая значению 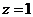 .
.
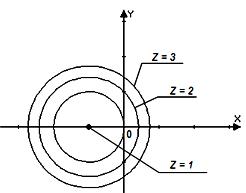 |
Рис. 4
Решение
а) 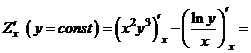
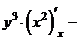
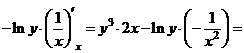
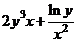 .
.
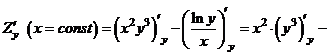
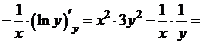
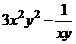 .
.
б) При фиксированном 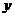 имеем показательную функцию
имеем показательную функцию
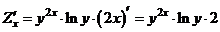 .
.
При фиксированном 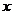 имеем степенную функцию
имеем степенную функцию
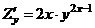 .
.
Упорядоченная пара частных производных 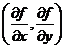 или
или 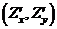 функции
функции 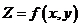 двух переменных обозначается символом
двух переменных обозначается символом 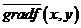 или
или 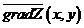 и называется градиентомфункции
и называется градиентомфункции 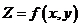 двух переменных. Градиент функции двух переменных есть двумерный вектор.
двух переменных. Градиент функции двух переменных есть двумерный вектор.
Градиент 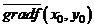 функции
функции 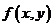 в точке
в точке 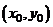 показывает направление самого быстрого роста функции
показывает направление самого быстрого роста функции 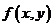 в точке
в точке 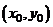 .
.
Пример 21. Для функции двух переменных 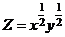 :
:
а) построить линию уровня, проходящую через точку (1; 9);
б) найти градиент в этой точке;
в) построить градиент.
Решение
а) Найдём уровень 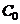 , который равен частному значению функции
, который равен частному значению функции 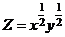 в точке (1; 9):
в точке (1; 9): 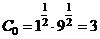 .
.
Уравнение линии уровня имеет вид
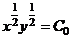 или
или 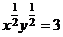 , или
, или 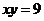 , или
, или 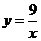 - гипербола
- гипербола
(рис. 5).
б) Найдём
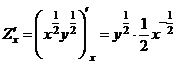 ,
, 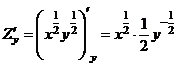 ,
,
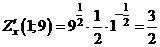 ,
, 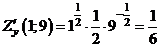 ,
,
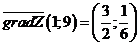 .
.
в) Строим вектор 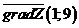 выходящим из точки
выходящим из точки 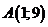 . Конец вектора в точке
. Конец вектора в точке 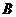 с координатами
с координатами
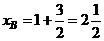 ,
, 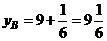 .
.
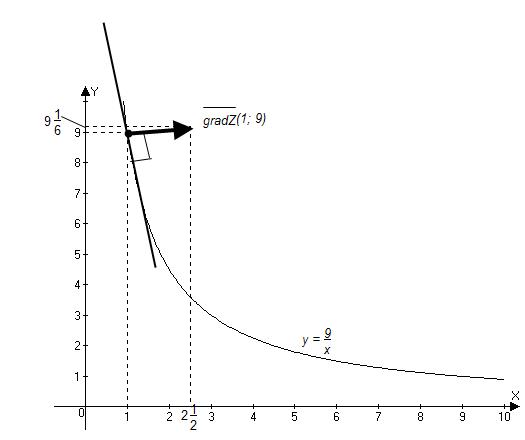 |
Рис. 5
Градиент 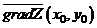 всегда перпендикулярен линии уровня
всегда перпендикулярен линии уровня 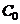 , проходящей через точку
, проходящей через точку 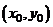 .
.
Решение
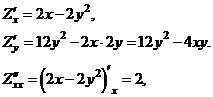
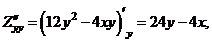
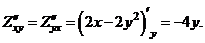
Решение
Найдём значение прибыли от реализации товара 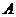 и
и 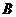 в объёмах
в объёмах 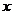 и
и 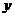 как разность между доходом от продажи
как разность между доходом от продажи 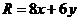 и издержками
и издержками 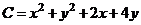 .
.
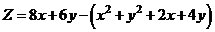 .
.
Определим стационарные точки функции. Найдём частные производные:
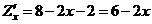 ,
, 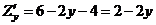 .
.
Решим систему:
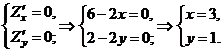
Точка 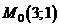 - стационарная точка функции.
- стационарная точка функции.
Найдём частные производные второго порядка:
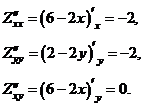
Учитывая что 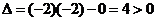 , а
, а 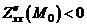 , определим:
, определим: 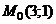 - точка максимума. Найдём максимальное значение прибыли
- точка максимума. Найдём максимальное значение прибыли 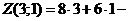
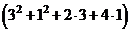
 .
.
 Условный экстремум
Условный экстремум
Экстремум функции 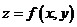 при условии, что
при условии, что 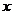 и
и 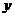 связаны уравнением
связаны уравнением 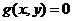 , называется условным экстремумом. Уравнение
, называется условным экстремумом. Уравнение 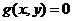 называется уравнением связи.
называется уравнением связи.
Для решения задач на условный экстремум обычно используется метод Лагранжа.
Составим вспомогательную функцию
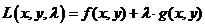 .
.
Функция 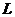 называется функцией Лагранжа, а
называется функцией Лагранжа, а 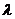 - множителем Лагранжа.
- множителем Лагранжа.
Точка условного экстремума является точкой локального экстремума функции Лагранжа , её координаты должны удовлетворять уравнениям
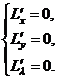
Пусть 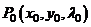 - любое решение этой системы и
- любое решение этой системы и
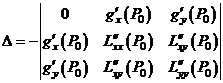 .
.
Если 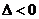 , то функция
, то функция 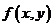 имеет в точке
имеет в точке 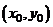 условный максимум, если
условный максимум, если 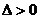 , то условный минимум.
, то условный минимум.
Пример 24. Найти экстремум 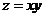 при условии
при условии 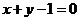 .
.
Решение
Функция Лагранжа имеет вид 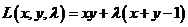 .
.
Найдём частные производные
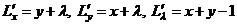 .
.
Решим систему
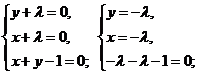
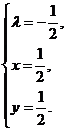
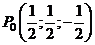 - «подозрительная» точка.
- «подозрительная» точка.
Наёдем частные производные
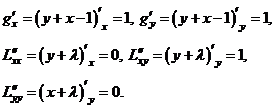
Вычислим определитель
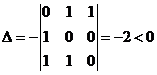 .
.
В точке 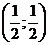 функция
функция 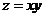 имеет условный экстремум
имеет условный экстремум
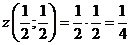 .
.
Метод наименьших квадратов
Пусть имеются данные наблюдений в 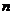 точках
точках  ,
, 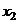 ,
, 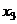 , …,
, …, 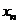 некоторой величины
некоторой величины 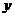 и получены соответствующие значения
и получены соответствующие значения 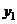 ,
, 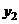 ,
, 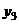 , …,
, …, 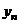 .
.
Необходимо подобрать функцию определённого вида 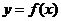 , чтобы она по возможности наиболее точно отражала общую зависимость измеряемой величины
, чтобы она по возможности наиболее точно отражала общую зависимость измеряемой величины 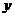 от параметров (координат) точек измерения
от параметров (координат) точек измерения 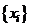 .
.
При обработке данных экономической статистики наиболее распространённым является приближение эмпирической формулой в виде линейной функции одной переменной 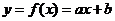 .
.
Неизвестные параметры эмпирической функции 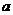 и
и 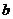 необходимо определить так, чтобы значения функции
необходимо определить так, чтобы значения функции 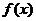 по возможности наименее всего отклонялись от измеренных значений.
по возможности наименее всего отклонялись от измеренных значений.
Метод наименьших квадратов состоит в минимизации суммы квадратов отклонений 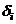 функции
функции 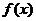 в точках
в точках 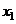 ,
, 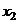 ,
, 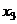 , …,
, …, 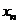 от измеренных значений
от измеренных значений 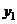 ,
, 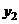 ,
, 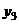 , …,
, …, 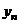 .
.
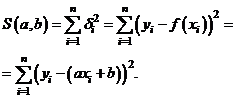
Для нахождения точки минимума функции 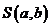 найдём частные производные этой функции по переменным
найдём частные производные этой функции по переменным 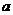 и
и 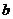 и приравняем их к нулю.
и приравняем их к нулю.
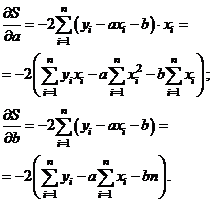
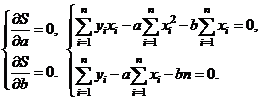
Коэффициенты 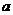 и
и 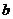 определяются из системы так называемых нормальных уравнений.
определяются из системы так называемых нормальных уравнений.
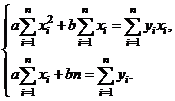
Пример 25. В результате эксперимента для пяти значений аргумента 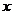 получены пять значений величины
получены пять значений величины 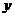 .
.
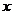 | -2 | ||||
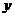 | 0,5 | 1,5 |
Методом наименьших квадратов найти функциональную зависимость между 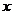 и
и 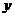 в виде линейной функции
в виде линейной функции 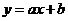 .
.
Решение
Значение параметров 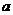 и
и 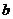 найдём из системы . Выполним необходимые вычисления:
найдём из системы . Выполним необходимые вычисления:
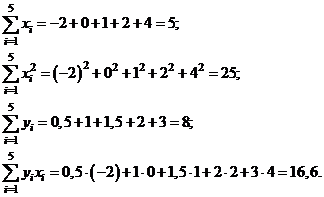
Запишем систему:
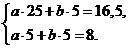
Решим систему по формулам Крамера:
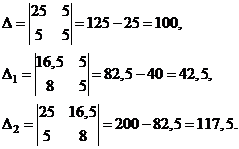
Значит 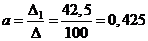 ,
, 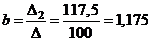 .
.
Функция имеет вид 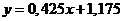 .
.
Основные понятия
Уравнение вида
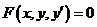 ,
,
где 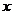 - независимая переменная;
- независимая переменная;
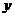 ,
, 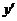 - неизвестная функция и её производная,
- неизвестная функция и её производная,
называется дифференциальным уравнением первого порядка.
В случае, когда из уравнения можно выразить 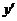 , оно имеет вид
, оно имеет вид
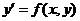 .
.
У<
