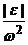Вектор скорости всегда направлен по касательной к траектории в сторону вращения (угловой скорости).
Вектор скорости всегда направлен по касательной к траектории в сторону вращения (угловой скорости).
Вывод:
Если мы знаем угловую скорость тела в данный момент времени, тогда для того чтобы найти скорость любой точки достаточно знать ее расстояние до оси. Умножив модуль угловой скорости на это расстояние, мы получим скорость любой точки данного тела.
Определение ускорения.
Для того чтобы определить ускорение точки, необходимо вспомнить, как определяется скорость точки.
Ускорение характеризует изменение скорости по времени. А скорость величина векторная. Она характеризуется модулем и направлением.
Поэтому одна составляющая ускорения учитывает, как меняется модуль скорости Wτ = 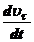 , а вторая величина Wn =
, а вторая величина Wn = 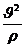 учитывает изменение скорости по направлению.
учитывает изменение скорости по направлению.
Вследствие, искривления траектории скорость 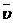 меняет модуль и направление. Поэтому вектор ускорения можно записать следующим образом:
меняет модуль и направление. Поэтому вектор ускорения можно записать следующим образом:
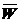 =
= 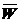 τ +
τ + 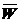 n
n
где
Wτ = 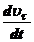 ; Wn =
; Wn = 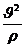
Для выбранной точки М h величина постоянная . Подставляя формулу (1) получаем:
Wτ = h 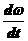
|
(3)
Теперь нормальное ускорение: вместо скорости подставляем его значение 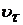 = h ω , а радиус кривизны окружности равен h
= h ω , а радиус кривизны окружности равен h
Получаем:
Wn = 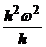 = hω2
= hω2
|
(4)
Введем новые обозначения, которые используются только для точек вращающегося тела.
Принимаем обозначения
Wω = h ε ( 3»)
Wω – центростремительное ускорение точки М, вектор данного ускорения всегда направлен по радиусу окружности к центру.
Wε 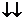 МС
МС
Wε = h ω2 ( 4»)
Wε - вращательное ускорение точки М, вектор данного ускорения всегда направлен по касательной к траектории в строну 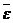 .
.
Wε 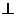 МС
МС
Т.к Wε 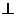 Wω , то модуль полного ускорения
Wω , то модуль полного ускорения
|
(5)
Необходимо указать величину, которая будет характеризовать направление этого вектора. Для этого изобразим следующие картинки.
Изображаем траекторию движения точки М и вектор скорости.
движение может быть ускорено или замедленно.
 |

Как бы не вращалось бы тело, центростремительное ускорение будет направлено в сторону вогнутости траектории, а вращательная составляющая направлена в сторону углового ускорения.
Полное ускорение определяется по правилу параллелограмма.
Теперь мы можем ввести угол α отклонения полного ускорения от радиуса.
Направление полного ускорения характеризует тангенс  угла
угла 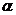 .
.
Из прямоугольного треугольника:
|
(6)
Выводы:
Заключение т.к. эти вектора равны по модулю и по направлению, тл они одинаковы.
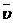 =
= 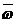
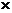
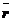 (8)
(8)
Формула (8) называется векторной формулой Эйлера.
Определение.
Последнюю формулу можно записать по-другому
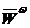 = - ω2
= - ω2 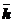
где 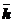 - радиус вектор точки М относительно центра окружности, описанной этой точкой.
- радиус вектор точки М относительно центра окружности, описанной этой точкой.
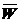 =
= 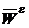 +
+ 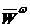
Вектор скорости всегда направлен по касательной к траектории в сторону вращения (угловой скорости).
Вывод:
Если мы знаем угловую скорость тела в данный момент времени, тогда для того чтобы найти скорость любой точки достаточно знать ее расстояние до оси. Умножив модуль угловой скорости на это расстояние, мы получим скорость любой точки данного тела.
Определение ускорения.
Для того чтобы определить ускорение точки, необходимо вспомнить, как определяется скорость точки.
Ускорение характеризует изменение скорости по времени. А скорость величина векторная. Она характеризуется модулем и направлением.
Поэтому одна составляющая ускорения учитывает, как меняется модуль скорости Wτ = 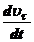 , а вторая величина Wn =
, а вторая величина Wn = 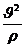 учитывает изменение скорости по направлению.
учитывает изменение скорости по направлению.
Вследствие, искривления траектории скорость 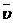 меняет модуль и направление. Поэтому вектор ускорения можно записать следующим образом:
меняет модуль и направление. Поэтому вектор ускорения можно записать следующим образом:
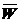 =
= 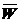 τ +
τ + 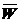 n
n
где
Wτ = 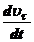 ; Wn =
; Wn = 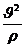
Для выбранной точки М h величина постоянная . Подставляя формулу (1) получаем:
Wτ = h 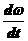
|
(3)
Теперь нормальное ускорение: вместо скорости подставляем его значение 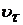 = h ω , а радиус кривизны окружности равен h
= h ω , а радиус кривизны окружности равен h
Получаем:
Wn = 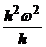 = hω2
= hω2
|
(4)
Введем новые обозначения, которые используются только для точек вращающегося тела.
Принимаем обозначения
Wω = h ε ( 3»)
Wω – центростремительное ускорение точки М, вектор данного ускорения всегда направлен по радиусу окружности к центру.
Wε 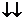 МС
МС
Wε = h ω2 ( 4»)
Wε - вращательное ускорение точки М, вектор данного ускорения всегда направлен по касательной к траектории в строну 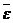 .
.
Wε 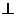 МС
МС
Т.к Wε 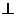 Wω , то модуль полного ускорения
Wω , то модуль полного ускорения
|
(5)
Необходимо указать величину, которая будет характеризовать направление этого вектора. Для этого изобразим следующие картинки.
Изображаем траекторию движения точки М и вектор скорости.
движение может быть ускорено или замедленно.
 |

Как бы не вращалось бы тело, центростремительное ускорение будет направлено в сторону вогнутости траектории, а вращательная составляющая направлена в сторону углового ускорения.
Полное ускорение определяется по правилу параллелограмма.
Теперь мы можем ввести угол α отклонения полного ускорения от радиуса.
Направление полного ускорения характеризует тангенс  угла
угла 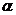 .
.
Из прямоугольного треугольника:
|
(6)
Выводы:

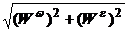 = h
= h 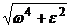
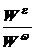 =
=