Построение графиков функций, не являющихся элементарными
Определение функции не предполагает, что функция обязательно задается одной формулой. Может оказаться так, что на различных участках изменения аргумента функция задаетя различными аналитическими выражениями. Приведем некоторые примеры.
Пример 4. Поcтроить график функции сигнум, которая задается выражением
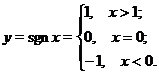
Решение. Если 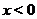 , то функция задана равенством
, то функция задана равенством 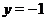 и ее графиком будет полупрямая, параллельная оси
и ее графиком будет полупрямая, параллельная оси  , причем точка
, причем точка 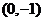 не будет принадлежать графику сигнума (будет выколотой). Для значений
не будет принадлежать графику сигнума (будет выколотой). Для значений 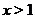 функция
функция 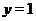 и ее графиком будет полупрямая, параллельная оси
и ее графиком будет полупрямая, параллельная оси 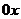 , причем точка
, причем точка 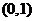 будет выколотой. При
будет выколотой. При 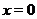 сигнум тоже равен нулю, поэтому на графике следует изобразить точку
сигнум тоже равен нулю, поэтому на графике следует изобразить точку 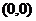 . Таким образом, сигнум является кусочно-постоянной функцией. Его график изображен на рис. 14.
. Таким образом, сигнум является кусочно-постоянной функцией. Его график изображен на рис. 14.
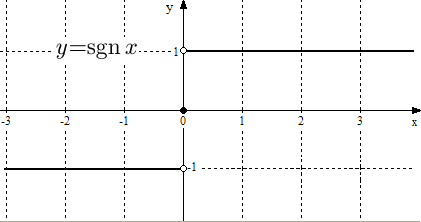
Рис. 14. График функции 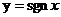 .
.
Пример 5. Пусть 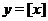 , где
, где 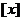 обозначает наибольшее целое чило, не превосходящее
обозначает наибольшее целое чило, не превосходящее 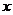 . Функция
. Функция 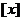 называется целой чаcтью числа
называется целой чаcтью числа 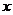 . Построить график
. Построить график 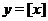 .
.
Решение. Если 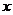 - целое число, то
- целое число, то 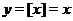 . Если
. Если 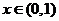 , то
, то 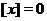 , если
, если 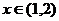 , то
, то 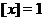 и т.д. Рассмотрим отрицательные значения
и т.д. Рассмотрим отрицательные значения 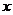 . Если
. Если 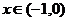 , то
, то 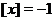 , если
, если 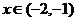 , то
, то 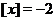 и т.д. График функции
и т.д. График функции 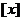 показан на рис. 15. Отметим, что левые концы сплошных отрезков принадлежат графику, а правые - не принадлежат.
показан на рис. 15. Отметим, что левые концы сплошных отрезков принадлежат графику, а правые - не принадлежат.
Пример 6. Построить график функции 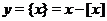 . Функция
. Функция 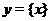 называется дробной частью числа
называется дробной частью числа 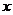 .
.
Решение. Дробная часть числа 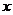 удовлетворяет неравенствам
удовлетворяет неравенствам 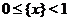 . Если
. Если 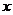 целое, то, очевидно, его дробная часть равна нулю:
целое, то, очевидно, его дробная часть равна нулю: 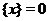 . При
. При 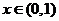 получим
получим 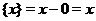 , при
, при 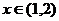 имеем
имеем 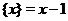 , при
, при 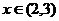 получим
получим 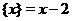 и т.д. Если
и т.д. Если 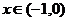 , то
, то 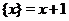 . Если
. Если 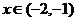 , то
, то 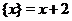 и т.д. График функции
и т.д. График функции 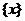 изображен на рис. 16. Заметим, что левые концы сплошных отрезков принадлежат графику, а правые - не принадлежат.
изображен на рис. 16. Заметим, что левые концы сплошных отрезков принадлежат графику, а правые - не принадлежат.
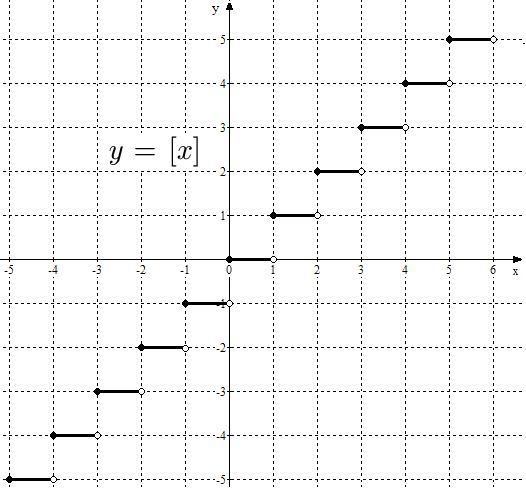
Рис. 15. График функции 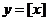 .
.
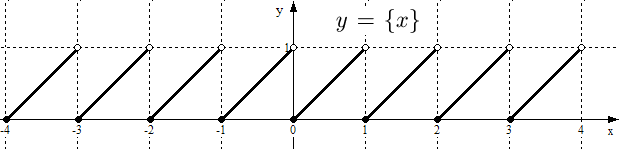
Рис. 16. График функции 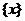 .
.
Пример 7. Построить график функции, определенной равенством
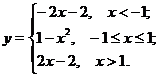
Решение. Функция 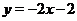 задает прямую, проходящую через точки
задает прямую, проходящую через точки 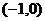 и
и 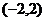 . Изобразим эту прямую при
. Изобразим эту прямую при 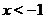 . Функция
. Функция 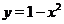 - это парабола, ветви которой направлены вниз. Её вершина находится в точке (0,1). Парабола
- это парабола, ветви которой направлены вниз. Её вершина находится в точке (0,1). Парабола 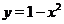 проходит через точки
проходит через точки 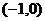 и
и 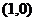 . Наконец, при
. Наконец, при 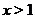 , изобразим прямую
, изобразим прямую 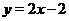 , проходящую через точки
, проходящую через точки 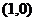 и
и 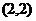 . Получим график непрерывной функции (см. рис. 17).
. Получим график непрерывной функции (см. рис. 17).
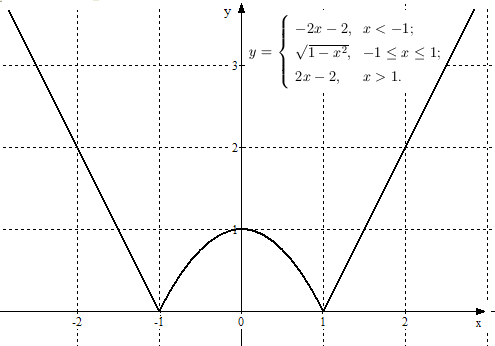
Рис. 17. К примеру 7.
4. Действия с графиками функций
В этом пункте мы рассмотрим сложение, вычитание, умножение и деление графиков функций. Также по графикам двух известных функций построим график суперпозиции этих функций.
4.1. Сложение и вычитание графиков
Сложение. Пусть даны две функции 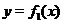 и
и 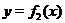 и их графики изветны. Требуется изобразить график функции
и их графики изветны. Требуется изобразить график функции 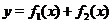 . Для этого построим на одном чертеже графики слагаемых функций. Затем проведем ряд вертикальных прямых, пересекающих графики этих функций, и пометим на них точки, ординаты которых равны сумме ординат слагаемых функций. Например (см. рис. 18), при
. Для этого построим на одном чертеже графики слагаемых функций. Затем проведем ряд вертикальных прямых, пересекающих графики этих функций, и пометим на них точки, ординаты которых равны сумме ординат слагаемых функций. Например (см. рис. 18), при 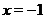 имеем
имеем 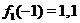 ,
, 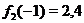 , значит
, значит 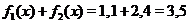 . Заметим, что при сложении нужно учитывать знак ординат, например, при
. Заметим, что при сложении нужно учитывать знак ординат, например, при 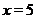 имеем
имеем 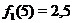 , а
, а 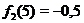 , значит
, значит 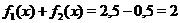 .
.
Соединяя полученные точки плавной кривой, получим эскиз графика функции 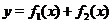 (см. рис. 18).
(см. рис. 18).
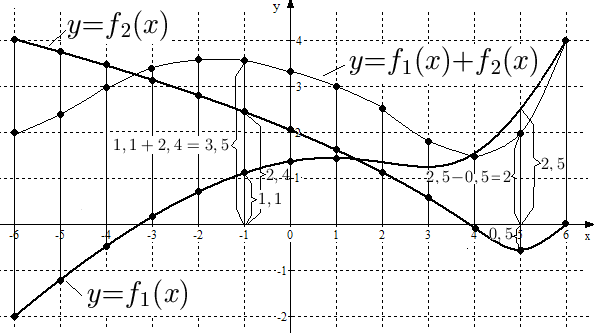
Рис. 18. Графики функций 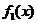 ,
, 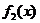 и
и 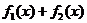 .
.
Вычитание. При построении эскиза графика разности двух функций 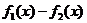 , графики которых известны можно либо сложить графики функций
, графики которых известны можно либо сложить графики функций 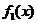 и
и 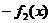 либо провести вертикальные прямые, пересекающих графики функций
либо провести вертикальные прямые, пересекающих графики функций 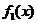 и
и 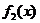 , и отметить на них точки, ординаты которых равны разности ординат функций
, и отметить на них точки, ординаты которых равны разности ординат функций 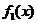 и
и 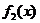 .
.
Пример 8. Построить график функции 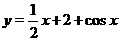 .
.
Решение. График функции 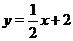 есть прямая, проходящая через точки
есть прямая, проходящая через точки 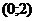 и
и 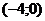 , график
, график 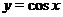 изображен на рис. 7. Построим график функции
изображен на рис. 7. Построим график функции 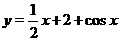 сложением графиков функций
сложением графиков функций 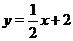 и
и 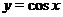 (см. рис. 19).
(см. рис. 19).
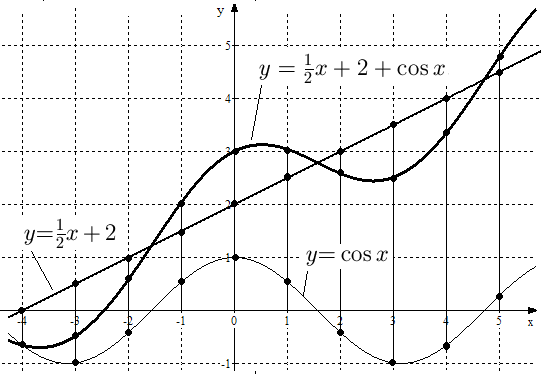
Рис. 19. Графики функций 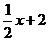 ,
, 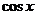 и
и 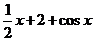 .
.
Пример 9. Построить график функции 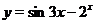 .
.
Решение. Построим графики функций 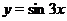 и
и 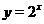 и вычтем график второй функции из графика первой (см. рис. 20). При этом, учитывая вид графика
и вычтем график второй функции из графика первой (см. рис. 20). При этом, учитывая вид графика 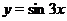 вертикальные прямые, пересекающие графики функций, будем проводить на расстоянии
вертикальные прямые, пересекающие графики функций, будем проводить на расстоянии 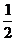 друг от друга.
друг от друга.
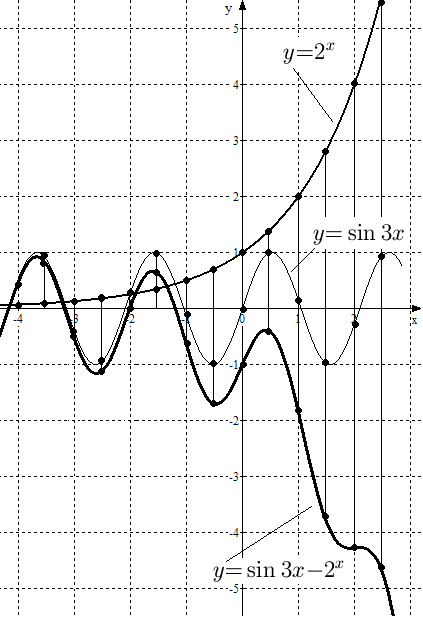
Рис. 20. Графики функций 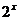 ,
, 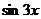 и
и 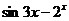 .
.
4.2. Умножение и деление графиков
Изучим правила перемножения и деления графиков функций. Рассмотрим как построить график суперпозиции двух функций. Приведем некоторые примеры.
Произведение. Пусть известны графики двух функций 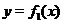 и
и 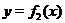 . Построим график функции
. Построим график функции 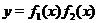 . Для этого изобразим на одном чертеже графики функций, входящих в произведение. Затем проведем ряд вертикальных прямых, пересекающих графики этих функций, и пометим на них точки, ординаты которых равны произведению ординат перемножаемых функций. При этом, если ордината одной их функций, входящих в произведение равна нулю, т.е. ее график пересекает ось
. Для этого изобразим на одном чертеже графики функций, входящих в произведение. Затем проведем ряд вертикальных прямых, пересекающих графики этих функций, и пометим на них точки, ординаты которых равны произведению ординат перемножаемых функций. При этом, если ордината одной их функций, входящих в произведение равна нулю, т.е. ее график пересекает ось 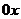 , то и ордината произведения будет равна нулю, т.е. график
, то и ордината произведения будет равна нулю, т.е. график 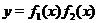 будет пересекать ось
будет пересекать ось 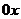 при том же значении абсциссы. Если ордината одной их функций
при том же значении абсциссы. Если ордината одной их функций 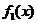 или
или 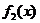 равна
равна 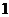 , то ордината произведения этих функций будет раположена на графике другой функции. Если перемножаются ординаты одного знака (либо обе ординаты имеют знак "
, то ордината произведения этих функций будет раположена на графике другой функции. Если перемножаются ординаты одного знака (либо обе ординаты имеют знак " 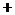 ", либо обе ординаты имеют знак "
", либо обе ординаты имеют знак " 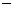 "), то произведение будет положительно. Если в произведение входят ординаты разных знаков (одна ордината имеет знак "
"), то произведение будет положительно. Если в произведение входят ординаты разных знаков (одна ордината имеет знак " 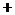 ", а другая "
", а другая " 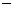 "), то их произведение будет отрицательно. Соединяя полученные точки плавной кривой, получим эскиз графика функции
"), то их произведение будет отрицательно. Соединяя полученные точки плавной кривой, получим эскиз графика функции 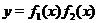 (см. рис. ).
(см. рис. ).
Например (см. рис. 21), при 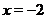 имеем
имеем 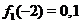 ,
, 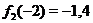 , значит
, значит 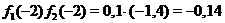 .
.
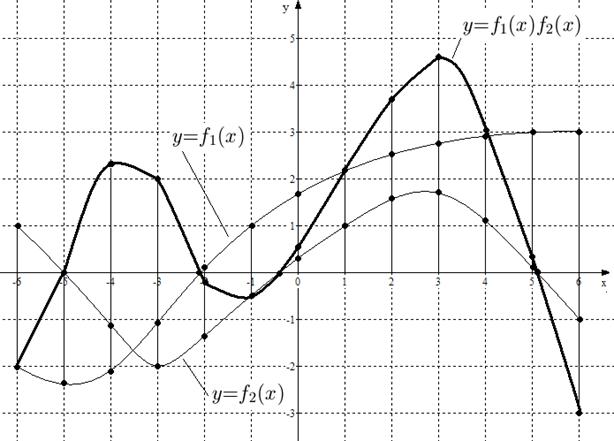
Рис. 21. Графики функций 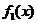 ,
, 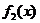 и
и 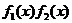 .
.
Пример 10. Построить график функции 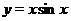 .
.
Решение. График функций 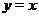 и
и 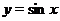 нам известны. График
нам известны. График 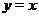 - бисектрисса первого и третьего координатных углов, а график
- бисектрисса первого и третьего координатных углов, а график 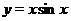 изображен на рис. 22. Заметим, что функция
изображен на рис. 22. Заметим, что функция 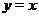 - нечётная и
- нечётная и 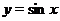 - нечётная, поэтому их произведение
- нечётная, поэтому их произведение 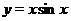 - чётная функция. Следовательно, достаточно построить график
- чётная функция. Следовательно, достаточно построить график 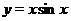 только для
только для 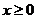 , а затем симметрично отобразить на полуплоскость
, а затем симметрично отобразить на полуплоскость 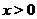 . Заметим также, что поскольку
. Заметим также, что поскольку 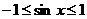 , то произведение
, то произведение 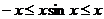 , т.е. график
, т.е. график 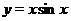 не выходит за пределы линий
не выходит за пределы линий 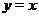 и
и 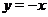 .
.
Итак, пусть 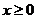 . В точках
. В точках 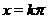 , где
, где 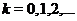 произведение
произведение 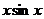 равно нулю, следовательно в этих точках график
равно нулю, следовательно в этих точках график 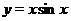 пересекает ось
пересекает ось 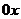 . Удобно также отметить точки, в которых
. Удобно также отметить точки, в которых 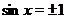 , поскольку при
, поскольку при 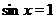 график
график 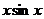 попадает на прямую
попадает на прямую 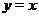 , а при
, а при 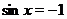 - на прямую
- на прямую 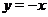 .
.
Проведя вертикальные прямые через точки 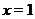 ,
, 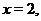 ...,
..., 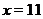 и перемножая соответствующие ординаты функций
и перемножая соответствующие ординаты функций 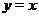 и
и 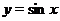 , получим график функции
, получим график функции 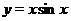 (см. рис. 22).
(см. рис. 22).
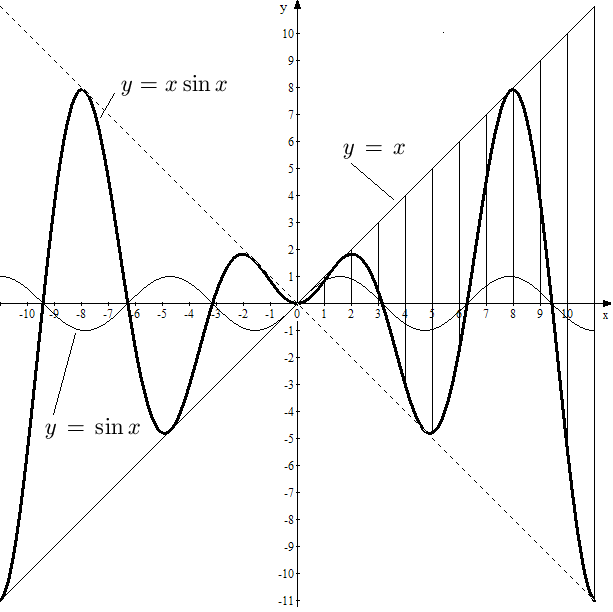
Рис. 22. Графики функций 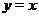 ,
, 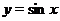 и
и 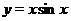 .
.
Частное.Теперь, зная графики функций 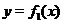 и
и 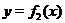 изобразим график функции
изобразим график функции 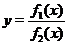 . Если знаменатель дроби
. Если знаменатель дроби 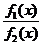 отличен от нуля:
отличен от нуля: 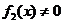 , то при делении графиков совершаются действия, аналогичные действиям при умножении графиков. А именно, изображаются графики
, то при делении графиков совершаются действия, аналогичные действиям при умножении графиков. А именно, изображаются графики 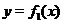 и
и  , проводится ряд вертикальных прямых, пересекающих эти графики, отмечаются точки, ординаты которых равны
, проводится ряд вертикальных прямых, пересекающих эти графики, отмечаются точки, ординаты которых равны  , полученные точки соединяются плавной линией (см. рис. 23).
, полученные точки соединяются плавной линией (см. рис. 23).
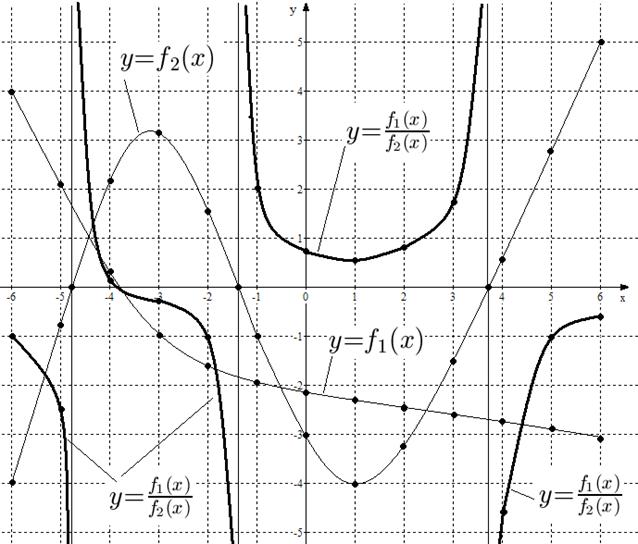
Рис. 23. Графики функций 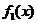 ,
, 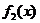 и
и 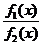 .
.
Точки, в которых 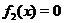 заслуживают особого внимания, поскольку в этих точках функция
заслуживают особого внимания, поскольку в этих точках функция 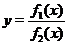 не существует. В окрестнотях точек, в которых знаменатель
не существует. В окрестнотях точек, в которых знаменатель 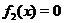 функция
функция 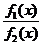 может вести себя по разному. Рассмотрим возможные варианты.
может вести себя по разному. Рассмотрим возможные варианты.
Пусть 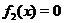 при
при 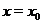 (
( 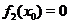 ). Возможны два случая:
). Возможны два случая: 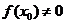 или
или 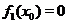 .
.
При 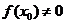 функция
функция 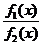 неограниченно возрастает или убывает в окрестности точки
неограниченно возрастает или убывает в окрестности точки 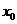 . В этом случае, нужно обратить внимание на знак частного
. В этом случае, нужно обратить внимание на знак частного 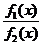 при
при 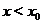 и при
и при 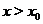 . Рассмотрим, например, правую окрестность, т.е. точки
. Рассмотрим, например, правую окрестность, т.е. точки 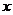 , которые больше
, которые больше 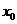 :
: 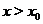 . Если при
. Если при 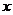 , достаточно близких к
, достаточно близких к 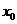 , таких, что
, таких, что 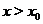 частное
частное 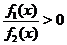 , то график функции
, то график функции 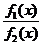 будет уходить вверх, прижимаясь справа к прямой
будет уходить вверх, прижимаясь справа к прямой 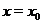 , но не пересекая её. Если же
, но не пересекая её. Если же 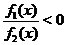 , то график
, то график 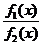 будет идти вниз, прижимаясь справа к прямой
будет идти вниз, прижимаясь справа к прямой 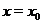 (см. рис. 23).
(см. рис. 23).
Аналогично поведет себя график 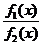 и в левой окрестности, т.е. при
и в левой окрестности, т.е. при 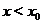 (только прижиматься к прямой
(только прижиматься к прямой 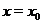 график будет слева) (см. рис. 23).
график будет слева) (см. рис. 23).
Ситуацию когда и 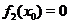 и
и 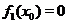 можно тщательно изучить только пользуясь теорией пределов, однако в некоторых случаях можно определить поведение функции
можно тщательно изучить только пользуясь теорией пределов, однако в некоторых случаях можно определить поведение функции 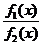 исходя из графиков
исходя из графиков 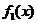 и
и 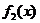 и в этом случае.
и в этом случае.
Отметим также, что для построения частного 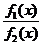 можно перемножить графики
можно перемножить графики 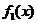 и
и 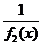 .
.
Замечание. При построении графиков произведения и частного двух функций полезно помнить, что если обе функции 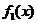 и
и 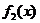 чётные или обе нечётные, то и произведение
чётные или обе нечётные, то и произведение 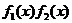 и частное
и частное 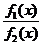 будет чётной функцией. Если же одна из функций
будет чётной функцией. Если же одна из функций 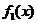 или
или 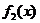 нечётная, а другая чётная, то их произведение
нечётная, а другая чётная, то их произведение 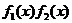 и частное будет нечётной функцией.
и частное будет нечётной функцией.
Пример 11.Построить график функции 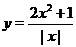 .
.
Решение. Используя рис. 2 и таблицу 1 изобразим графики функций 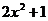 и
и 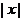 (см. рис. 24).
(см. рис. 24).
Функции 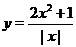 определена и непрерывна во всех точках, за исключением нуля.
определена и непрерывна во всех точках, за исключением нуля.
Заметим, что 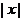 - четная функция, причем
- четная функция, причем 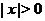 при
при 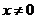 , функция
, функция 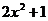 тоже четная, причем
тоже четная, причем 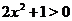 для всех
для всех 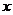 . Поэтому функция график
. Поэтому функция график 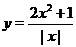 будет симметричен относительно оси
будет симметричен относительно оси 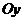 и расположен выше оси
и расположен выше оси 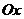 .
.
Построим график 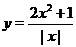 при
при 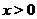 . Проведем вертикальные линии, проходящие через точки
. Проведем вертикальные линии, проходящие через точки 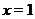 ,
, 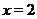 ,
, 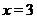 ,
, 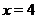 и отметим на них значение частного функций
и отметим на них значение частного функций 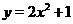 и
и 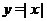 . Так при
. Так при 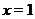 будем иметь
будем иметь 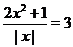 , при
, при 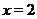 получим
получим 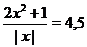 и т.д.
и т.д.
Замечая, что при 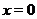 знаменатель дроби
знаменатель дроби 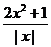 обращаетя в нуль, а числитель отличен от нуля (равен единице), и учитывая, что
обращаетя в нуль, а числитель отличен от нуля (равен единице), и учитывая, что 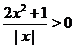 для всех
для всех 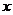 (значит, и в любой окрестности точки
(значит, и в любой окрестности точки 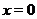 ) получим, что график рассматриваемой функции при
) получим, что график рассматриваемой функции при 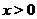 будет уходить вверх, прижимаясь справа к оси
будет уходить вверх, прижимаясь справа к оси 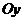 .
.
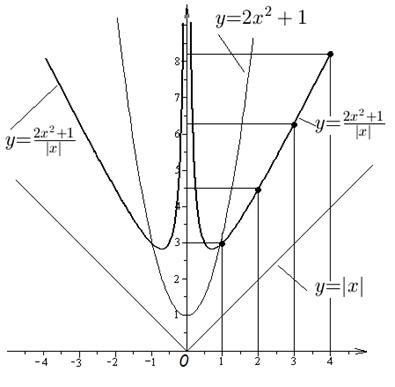
Рис. 24. Графики функций 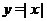 ,
, 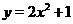 и
и 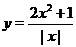 .
.
Соединяя отмеченные точки и рисуя график функции в промежетке от 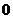 до
до 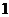 уходящим вверх и приближающимся справа к оси
уходящим вверх и приближающимся справа к оси 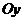 , получим график функции при
, получим график функции при 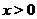 . В силу четности рассматриваемой функции, слева от оси
. В силу четности рассматриваемой функции, слева от оси 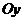 изображаем кривую, симметричную кривой справа от оси
изображаем кривую, симметричную кривой справа от оси 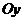 , получаем искомый график (см. рис. 24).
, получаем искомый график (см. рис. 24).
4.3. Построение графиков сложных функций
Суперпозиция. Пусть графики функций 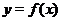 и
и 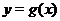 известны. Для того, чтобы изобразить график сложной функции (суперпозиции двух функций)
известны. Для того, чтобы изобразить график сложной функции (суперпозиции двух функций) 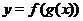 (см. рис. 25) составим таблицу (см. таблицу 2).
(см. рис. 25) составим таблицу (см. таблицу 2).
В первой строке таблицы запишем значения аргумента 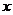 , при этом выберем интересующую нас область построения (на рис. 25 - это отрезок
, при этом выберем интересующую нас область построения (на рис. 25 - это отрезок 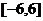 ) и значения аргумента будем брать на некотором расстоянии друг от друга (на рис. 25 мы берем точки
) и значения аргумента будем брать на некотором расстоянии друг от друга (на рис. 25 мы берем точки 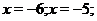 ...
... 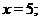
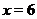 ).
).
Во вторую строку таблицы исходя из графика (если есть аналитическое выражение для 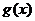 нужно использовать его) запишем значения внутренней функции
нужно использовать его) запишем значения внутренней функции 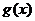 в соответствующих точках
в соответствующих точках 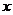 из первой строки (так в таблице 2 это
из первой строки (так в таблице 2 это 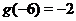 ;
; 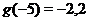 ;...;
;...; 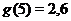 ;
; 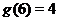 ).
).
В третьей строке таблицы запишем значения внешней функции 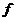 от значений
от значений 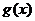 из второй строки (в таблице 2 это
из второй строки (в таблице 2 это 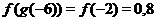 ;
; 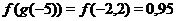 ;...;
;...; 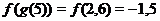 ;
; 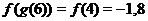 ).
).
На график нанесем точки с координатами 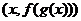 из первой и третьей строк таблицы и соединим их плавной линией. Получим эскиз графика
из первой и третьей строк таблицы и соединим их плавной линией. Получим эскиз графика 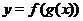 (см. рис. 25).
(см. рис. 25).
Таблица 2.
 | 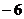 | 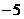 | 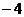 | 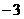 | 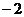 | 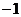 | 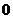 |
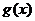 | 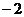 | 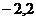 | 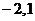 | 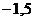 | 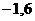 | 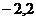 | 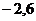 |
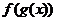 | 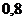 | 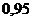 | 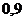 | 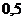 | 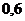 | 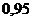 | 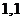 |
Продолжение таблицы 2.
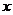 | 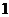 | 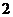 | 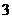 | 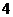 | 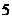 | 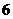 |
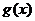 | 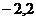 | 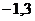 | 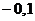 | 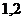 | 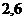 | 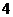 |
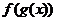 | 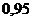 | 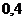 | 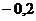 | 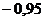 | 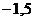 | 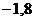 |
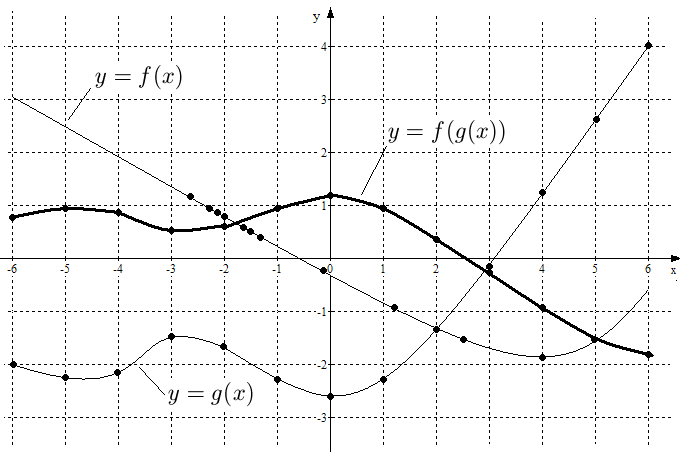
Рис. 25. Графики функций 
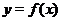 и
и 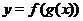 .
.
Пример 12. Построить эскиз графика 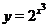 .
.
Решение. Функция 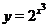 является суперпозицией функций
является суперпозицией функций 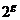 и
и 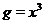 . Областью определения функции
. Областью определения функции 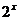 , как и функции
, как и функции 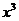 является вся числовая ось. Поэтому областью определения функции
является вся числовая ось. Поэтому областью определения функции 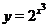 также является вся числовая ось. Очевидно, что
также является вся числовая ось. Очевидно, что 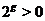 при любых
при любых 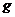 , поэтому график будет расположен полностью выше оси
, поэтому график будет расположен полностью выше оси 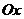 .
.
Составим таблицу, в первой строке которой укажем значения аргумента 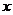 (рассмотрим значения от
(рассмотрим значения от 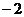 до
до 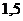 с шагом в половину единичного отрезка), во второй - значения функции
с шагом в половину единичного отрезка), во второй - значения функции 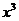 при соответствующих значениях аргумента, в третьей - значения
при соответствующих значениях аргумента, в третьей - значения 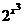 .
.
Таблица 3.
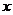 | 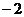 | 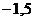 | 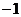 | 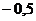 | 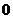 | 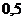 | 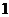 | 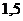 |
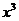 | 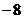 | 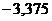 | 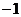 | 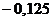 | 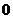 | 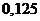 | 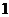 | 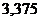 |
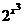 | 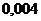 | 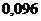 | 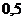 | 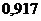 | 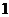 | 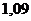 | 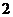 | 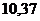 |
Отметим точки, соответствующие первой и третьей строкам таблицы 3, на чертеже, соединим их плавной линией и получим эскиз графика функции 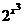 (см. рис. 26)
(см. рис. 26)
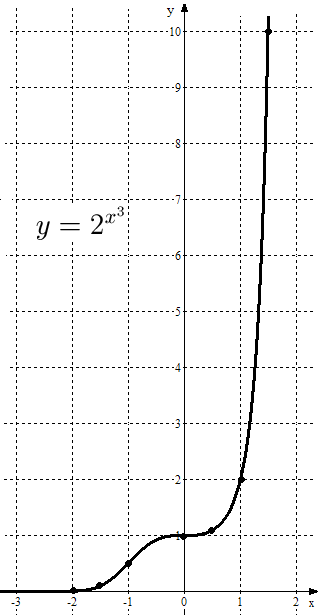
Рис. 26. График функции 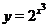 .
.
Пример 13.Построить эскиз графика 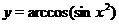 .
.
Решение. Данная функция определения для всех значений 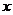 . В силу (1), её областью значений является отрезок
. В силу (1), её областью значений является отрезок 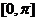 . Поскольку
. Поскольку
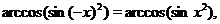
то функция 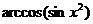 является четной и достаточно построить её график в области
является четной и достаточно построить её график в области 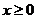 .
.
Используя равенство (3), получим
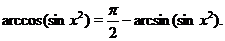
Вспомним, что функция 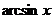 является обратной к
является обратной к 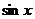 только при
только при 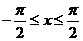 . Следовательно,
. Следовательно,  при
при 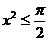 , т.е. при
, т.е. при 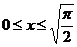 (мы взяли
(мы взяли 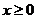 по причине четности рассматриваемой функции).
по причине четности рассматриваемой функции).
Имеем, что при 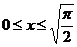 выполняется равенство
выполняется равенство 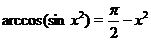 .
.
Если 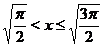 , то
, то 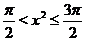 и, отняв из неравенств
и, отняв из неравенств 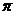 , получим
, получим 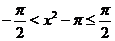 . Учитывая, что
. Учитывая, что 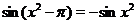 будем иметь
будем иметь
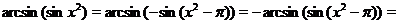
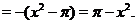
Поэтому при 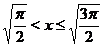 график функции
график функции 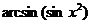 совпадает с графиком функции
совпадает с графиком функции 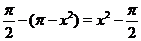 (см. рис. 27).
(см. рис. 27).
При 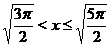 получаем, что
получаем, что 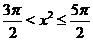 и
и 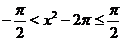 . Поскольку
. Поскольку  , то на указанном промежутке
, то на указанном промежутке 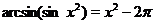 . Следовательно, при
. Следовательно, при 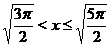 график функции
график функции 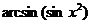 совпадает с графиком функции
совпадает с графиком функции 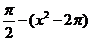 (см. рис. 27).
(см. рис. 27).
Аналогично при 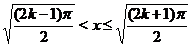 ,
, 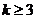 , имеем, что график исходной функции совпадет с графиком функции
, имеем, что график исходной функции совпадет с графиком функции
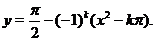
Начертив график функции 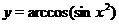 при
при 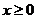 , симметрично изобразим его и при
, симметрично изобразим его и при 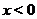 . Эскиз графика функции
. Эскиз графика функции 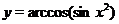 представлен на рис. 27.
представлен на рис. 27.
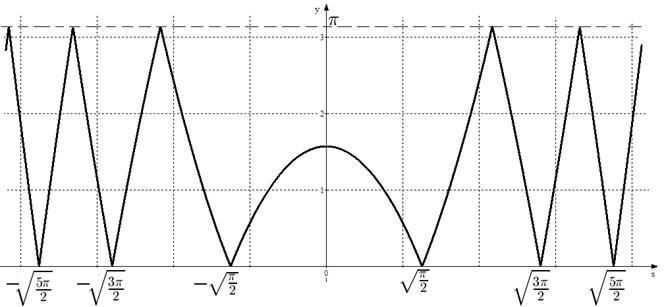
Рис. 27. График функции 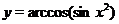 .
.
5. Графики в полярных координатах
5.1. Полярные координаты
Положение точки 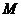 в полярных координатах на плоскости (см. рис. 28) определяется:
в полярных координатах на плоскости (см. рис. 28) определяется:
1) ее расстоянием 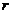 от некоторой данной точки
от некоторой данной точки 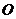 , называемой полюсом;
, называемой полюсом;
2) углом 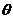 , который образует отрезок
, который образует отрезок  с заданным направлением прямой
с заданным направлением прямой  , которая называется полярной осью).
, которая называется полярной осью).
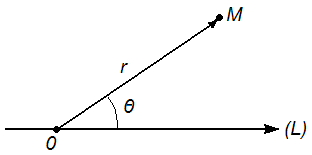
Рис. 28. Точка  в полярных координатах.
в полярных координатах.
При этом 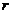 называют радиусом-вектором и
называют радиусом-вектором и 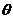 - полярным углом. Если принять полярную ось за
- полярным углом. Если принять полярную ось за 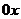 , а полюс - за начало координат, то имеем, очевидно (см. рис. 29):
, а полюс - за начало координат, то имеем, очевидно (см. рис. 29): 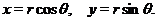
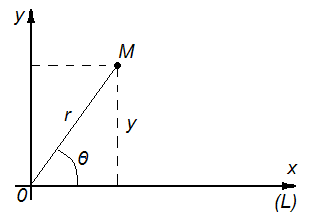
Рис. 29. Точка 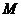 в полярных координатах.
в полярных координатах.
Данному положению точки 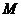 соответствует одно определенное положительное значение
соответствует одно определенное положительное значение  и бесчисленное множество значений
и бесчисленное множество значений 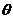 , которые отличаются слагаемым, кратным
, которые отличаются слагаемым, кратным 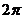 . Если
. Если 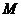 совпадает с
совпадает с 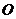 , то
, то 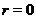 и
и 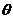 - неопределенно.
- неопределенно.
Всякая функциональная зависимость вида 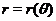 (явная) или
(явная) или 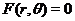 (неявная) имеет в полярной системе координат свой график.
(неявная) имеет в полярной системе координат свой график.
В дальнейшем мы будем рассматривать не только положительные, но и отрицательные значения 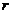 , причем если некоторому значению
, причем если некоторому значению 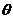 соответствует отрицательное значение
соответствует отрицательное значение 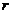 , то условимся откладывать это значение
, то условимся откладывать это значение 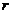 в направлении, прямо противоположном тому направлению, которое определяется значением
в направлении, прямо противоположном тому направлению, которое определяется значением 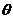 .
.
5.2. Графики кривых в полярных координатах
Для того, чтобы построить график 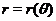 в полярных координатах по точкам нужно заполнить таблицу, в первой строке которой записать значения угла
в полярных координатах по точкам нужно заполнить таблицу, в первой строке которой записать значения угла 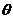 из интересующего промежутка, а во второй - соответствующие значения функции
из интересующего промежутка, а во второй - соответствующие значения функции 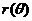 . Затем, отметить и соединить эти точки плавной ли<
. Затем, отметить и соединить эти точки плавной ли<
