Часть 1. Построение эскизов графиков функций

ГРАФИКИ ФУНКЦИЙ

Учебно-методическое пообие для вузов

Составители:

П.С. Украинский,

А.И. Шашкин,

Э.Л. Шишкина

Издателько-полиграфический центр

Воронежского государственного университета

Утверждено научно-методическим советом факультета прикладной математики, информатики и механики 25 мая 2011 г., протокол № 10.

Рецензент д-р физ. мат. наук, профессор А. Д. Баев

Учебно-методическое пособие по дисциплине "Математический анализ" подготовлено на кафедре математического и прикладного анализа факультета прикладной математики, информатики и механики Воронежского государственного университета

Рекомендуется для студентов первого курса очной и очно-заочной форм обучения

Для направлений 010400.62 "Прикладная математика и информатика", 010300.62 "Фундаментальная информатика и информационные технологии", 010500 "Математическое обеспечение и администрирование информационных систем", 080500.62 "Бизнес-информатика", 010800.62 "Механика и математическое моделирование".

Оглавление

Часть 1. Построение эскизов графиков функций. 4

1. Графики основных элементарных функций……………………………………... 4

1.1. Постоянная и степенная функции. 5

1.2. Показательная и логарифическая функции. 8

1.3. Тригонометрические функции. 9

1.4. Обратные тригонометрические функции. 11

2. Элементарные преобразования графиков……………………………………… 12

3. Построение графиков функций, не являющихся элементарными……………. 16

4. Действия с графиками функций………………………………………………… 19

4.1. Сложение и вычитание графиков. 19

4.2. Умножение и деление графиков. 22

4.3. Построение графиков сложных функций. 28

5. Графики в полярных координатах……………………………………………… 32

5.1. Полярные координаты.. 32

5.2. Графики кривых в полярных координатах. 33

Часть 2. Применение дифференциального исчисления к исследованию функций и построению их графиков. 38

1. Признак возрастания и убывания функции…………………………………….. 38

2. Локальные экстремумы функции……………………………………………….. 39

3. Выпуклость функции. Точки перегиба…………………………………………. 43

4. Асимптоты………………………………………………………………………... 48

5. Порядок построения графика функции, заданной выражением 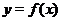…….. 49

6. Построение графика функции, заданной параметрически……………………. 53

6.1. Порядок построения графика параметрически заданной функции. 53

6. 2. Асимптоты параметрического графика. 54

6. 3. Точки перегиба. 54

6.4. Пример построения графика параметрически заданной функции. 55

Список литературы.. 58

Введение

Методическое пособие составлено из двух частей: в первой части рассматривается построение эскизов графиков функций, во второй - построение графиков функций с использованием техники дифференцирования. Для построения эскизов графиков функций применяются следующие приемы: построение "по точкам", действия с графиками (например, сложение, вычитание, умножение графиков), преобразование графиков.

Часть 1. Построение эскизов графиков функций

В этой части мы будем изучать построение графиков функций, используя наименьшее число вычисление и избегая прямого применения дифференциального исчисления. Такие эскизы иллюстрируют общее поведение функции и полезны при решении различных задач.

В первом разделе этой части мы построим графики основных элементарных функций в прямоугольной декартовой системе координат и отметим некоторые особенности поведения этих функций.

Во втором разделе изучим элементарные преобразования графиков функций, таких как параллельный перенос, поворот, зеркальное отображение, растяжение, сжатие и др.

В третьем разделе построим графики некоторых функций, не являющихся элементарными.

В четвертом разделе разберем как производить сложение, вычитание, умножение и деление графиков, а также как строить график сложной функции.

В пятом разделе мы рассмотрим полярную систему координат и построим в ней графики некоторых функций, наиболее часто встречающихся в приложениях.

Тригонометрические функции

Тригонометрические функции и опредены на всей числовой оси, переодические, с периодом 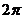и не принимают значения по абсолютной величине большие 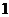. Отметим также, что функция является нечетной, а функция - четной. Их графики изображены на рис. 7.

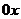Линия, являющаяся графиком функции , называется синусоидой. График функции - тоже синусоида, она получается из графика смещением вдоль влево на отрезок .

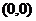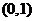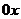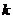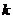Из рис. 7 видно, что график функции проходит через точку - начало координат, а функция проходит через точку . Графики обеих функций и и пересекают ось неограниченное число раз, это означает, что уравнения и имеют бесконечно много корней. Именно, решение уравнения имеет вид , где - целое число, а решением уравнения будут число , где - целое число.

Рис. 7. Графики функции и .

Тангенс и котангенс выражаются формулами и , а в такой форме записи видно, что графики этих функций будут иметь бесконечно много точек разрыва. Действительно, у 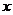в знаменателе находится 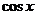, который обращается в нуль в точках , а 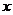будет иметь разрывы там, где синус равен нулю, т.е. в точках ( 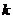- целое число).

Обе функции и и являются нечетными и периодическими с периодом 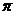. Графики этих функций приведены на рис. 8.

Рис. 8. Графики функции и .

Список литературы

1. Данко П. Е. Высшая математика в упражнениях и задачах в двух частях, часть I, издание четвертое, исправленное и дополненное // П. Е. Данко, А. Г. Попов, Т. Я. Кожевникова. - М: "Высшая школа", 1986.

2. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления // Г.М. Фихтенгольц. T.1. - СПб: Лань, 1997.

3. Смирнов В. И. Курс высшей математики // В. И. Смирнов. Т.1. - М: Наука, Гл. ред. физ.-мат. лит., 1974.

4. Савелов А. А. Замечательные кривые // А. А. Савелов. - Томск: Красное знамя, 1938.

5. Савелов А. А. Плоские кривые // А. А. Савелов. - М: ГИФМЛ, 1960.

6. Виноградова И. А. Задачи и упражнения по математическому анализу. В 2-х кн. Кн. 1. Дифференциальное и интегральное исчисление функций одной переменной: Учеб. пособие.– 2-е изд., перераб. / И. А. Виноградова, С. Н. Олехник, В. А. Садовничий. Под ред. В. А. Садовничего. – М: Высш. шк., 2000.

7. Каплан И. А. Практические занятия по высшей математике // И. А. Каплан. - Харьков: изд-во Харьковского ордена трудового красного знамени гос. ун-та им. А. М. Горького, 1967.

8. Харди Г. Х. Курс чистой математики // Г. Х. Харди. - М: гос. изд-во иностр. лит., 1949.

ГРАФИКИ ФУНКЦИЙ

Учебно-методическое пообие для вузов

Составители:

П.С. Украинский,

А.И. Шашкин,

Э.Л. Шишкина

Издателько-полиграфический центр

Воронежского государственного университета

Утверждено научно-методическим советом факультета прикладной математики, информатики и механики 25 мая 2011 г., протокол № 10.

Рецензент д-р физ. мат. наук, профессор А. Д. Баев

Учебно-методическое пособие по дисциплине "Математический анализ" подготовлено на кафедре математического и прикладного анализа факультета прикладной математики, информатики и механики Воронежского государственного университета

Рекомендуется для студентов первого курса очной и очно-заочной форм обучения

Для направлений 010400.62 "Прикладная математика и информатика", 010300.62 "Фундаментальная информатика и информационные технологии", 010500 "Математическое обеспечение и администрирование информационных систем", 080500.62 "Бизнес-информатика", 010800.62 "Механика и математическое моделирование".

Оглавление

Часть 1. Построение эскизов графиков функций. 4

1. Графики основных элементарных функций……………………………………... 4

1.1. Постоянная и степенная функции. 5

1.2. Показательная и логарифическая функции. 8

1.3. Тригонометрические функции. 9

1.4. Обратные тригонометрические функции. 11

2. Элементарные преобразования графиков……………………………………… 12

3. Построение графиков функций, не являющихся элементарными……………. 16

4. Действия с графиками функций………………………………………………… 19

4.1. Сложение и вычитание графиков. 19

4.2. Умножение и деление графиков. 22

4.3. Построение графиков сложных функций. 28

5. Графики в полярных координатах……………………………………………… 32

5.1. Полярные координаты.. 32

5.2. Графики кривых в полярных координатах. 33

Часть 2. Применение дифференциального исчисления к исследованию функций и построению их графиков. 38

1. Признак возрастания и убывания функции…………………………………….. 38

2. Локальные экстремумы функции……………………………………………….. 39

3. Выпуклость функции. Точки перегиба…………………………………………. 43

4. Асимптоты………………………………………………………………………... 48

5. Порядок построения графика функции, заданной выражением 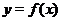…….. 49

6. Построение графика функции, заданной параметрически……………………. 53

6.1. Порядок построения графика параметрически заданной функции. 53

6. 2. Асимптоты параметрического графика. 54

6. 3. Точки перегиба. 54

6.4. Пример построения графика параметрически заданной функции. 55

Список литературы.. 58

Введение

Методическое пособие составлено из двух частей: в первой части рассматривается построение эскизов графиков функций, во второй - построение графиков функций с использованием техники дифференцирования. Для построения эскизов графиков функций применяются следующие приемы: построение "по точкам", действия с графиками (например, сложение, вычитание, умножение графиков), преобразование графиков.

Часть 1. Построение эскизов графиков функций

В этой части мы будем изучать построение графиков функций, используя наименьшее число вычисление и избегая прямого применения дифференциального исчисления. Такие эскизы иллюстрируют общее поведение функции и полезны при решении различных задач.

В первом разделе этой части мы построим графики основных элементарных функций в прямоугольной декартовой системе координат и отметим некоторые особенности поведения этих функций.

Во втором разделе изучим элементарные преобразования графиков функций, таких как параллельный перенос, поворот, зеркальное отображение, растяжение, сжатие и др.

В третьем разделе построим графики некоторых функций, не являющихся элементарными.

В четвертом разделе разберем как производить сложение, вычитание, умножение и деление графиков, а также как строить график сложной функции.

В пятом разделе мы рассмотрим полярную систему координат и построим в ней графики некоторых функций, наиболее часто встречающихся в приложениях.