Теорема Ролля, ее геометрический смысл

Теорема: если функция y=f(x) непрерывна на отрезке [a,b], и 1. Имеет конечную производную f’(x), x ϵ (a,b), 2. f(a) = f(b), тогда Ǝ точка с ϵ (a,b) такая что f’(c) = 0.

Доказательство: По 2-ой теореме Вейерштрасса f(x) достигает наибольшего значения на [a,b]. Пусть М – наибольшее значение f(x), m – наименьшее значение f(x) на [a,b].

1. M=m так как f(a)=f(b) f(x)=f(a)=f(b)=const и условие f’(x) = 0 выполняется для любых хϵ(a,b).

2. M≠m f(x) не может принимать наибольшего(наименьшего) значения при x=a(x=b) то есть Ǝ точка cϵ(a,b) для которой f(x) =max(min) по т.Ферма в этой точке f’( c ) =0.

Из теоремы Ролля следует, что существует точка х=с, на отрезке [a,b], в которой касательная к графику функции f(x) параллельна оси ox.

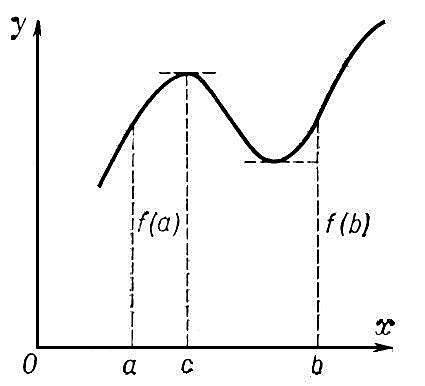
Билет №24

Теорема Лагранжа о конечном приращении функции, ее геометрический смысл

Пусть функция f(x):

1. Непрерывна на отрезка [a,b]

2. Дифференцируема в интервале (a,b)

Тогда существует точка x=c на отрезке [a,b] такая, что f(b) – f(a) = f '(c)(b-a)

Существует точка x=c на отрезке (a,b), в которой касательная к графику функции f(x) параллельная прямой, проходящей через хорду графика или совпадающая с ней.

Доказательство: Рассмотрим вспомогательную функцию F(x) =f(x) – f(a) - 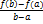(x-a) (1)

Функция (1) удовлетворяет всем условиям т.Ролля F(b)=F(a) F(b)=0, F(a)=0.

Это значит, что существует т сϵ(a,b), для которой F’(c) = 0.

F’(x) = f(x) -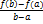

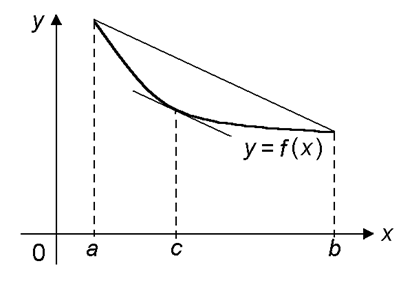
F’(c) = f’(c) – 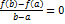=> f’(c) =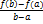

Билет №25

Теорема Лапиталя, ее использование для раскрытия неопределенностей при нахождении пределов

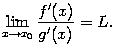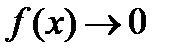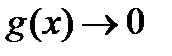Пусть функции f(x) и g(x) непрерывны в некоторой окрестности Е точки x₀ и f(x₀)=g(x₀)=0, то есть и при 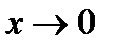. Предположим, что при 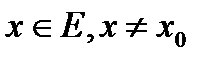функции f(x) и g(x) имеют производные f'(x) и g'(x), причём существует предел отношения этих производных:

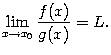Тогда предел отношения самих функций f(x) и g(x) тоже существует и равен тому же числу L :

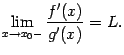
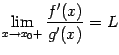Доказательство. Заметим, что из условия следует, что оба односторонних предела также равны L :

И

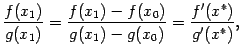Пусть x₁ , . По теореме Коши, применённой к отрезку [x₀;x₁], получим тогда, с учётом того, что f(x₀)=0, g(x₀)=0,

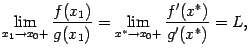где 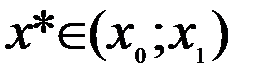. Перейдём теперь в этом равенстве к пределу при :

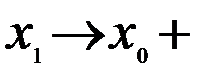так как, очевидно, при 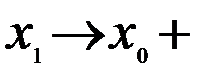имеем также 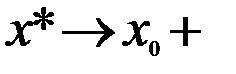. Теперь возьмём точку x₂ 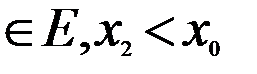, и применим теорему Коши к отрезку [x₂;x₀]. Получим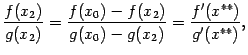

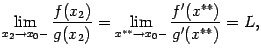где x** 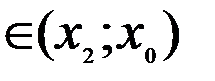Переходя к пределу при 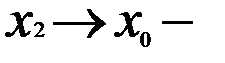, получаем

так как при 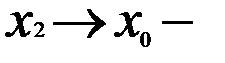имеем 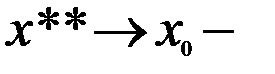. Итак, оба односторонних предела отношения 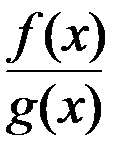равны L . На основании теоремы о связи односторонних пределов с двусторонним получаем, что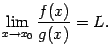

Билет №26

Теорема Тейлора

Пусть функцияr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> 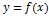определена в некоторой точке x=a и в некоторой окрестности этой точки функция имеет производные до 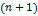-го порядка, тогда существует точка x=Ɛ, такая, что выполняется формула Тейлора

, причем точка Ɛ лежит между x и a, т.е. .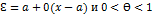

Последнее слагаемое в формуле Тейлора называется остаточным членом в форме Лагранжа.

При 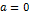формула Тейлора называется формулой Маклорена:

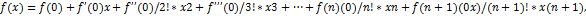
Билет №27

Формула Маклорена

Формулой Маклоренаназывается формула Тейлора при r wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>">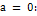

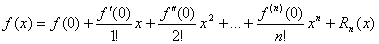
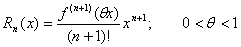
Мы получили так называемую формулу Маклорена с остаточным членом в форме Лагранжа.

Следует отметить, что при разложении функции в ряд применение формулы Маклорена предпочтительнее, чем применение непосредственно формулы Тейлора, т.к. вычисление значений производных в нуле проще, чем в какой- либо другой точке, естественно, при условии, что эти производные существуют.

Однако, выбор числа а очень важен для практического использования. Дело в том, что при вычислении значения функции в точке, расположенной относительно близко к точке а, значение, полученное по формуле Тейлора, даже при ограничении тремя – четырьмя первыми слагаемыми, совпадает с точным значением функции практически абсолютно. При удалении же рассматриваемой точки от точки а для получения точного значения надо брать все большее количество слагаемых формулы Тейлора, что неудобно.

Т.е. чем больше по модулю значение разности 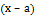тем более точное значение функции отличается от найденного по формуле Тейлора.

Кроме того, можно показать, что остаточный член R_n+1(x) является бесконечно малой функцией при ха, причем долее высокого порядка, чем (х – а)^m, т.е.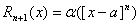

Таким образом, ряд Маклорена можно считать частным случаем ряда Тейлора.

Билет №28

Интервалы монотонности

Функция 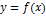возрастает(убывает) на интервале 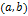, если для 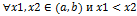следует неравенство 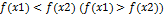. Функция 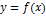не возрастает (не убывает) на интервале 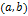, если для 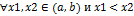следует неравенство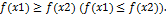

Теорема. Если 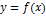дифференцируема на 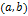и 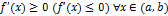, то функция 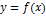не убывает (не возрастает) на данном интервале.

Билет №29