Потери напора на трение по длине потока.

Рассмотрим кольцевой слой жидкости толщины dr на расстоянии r от оси трубы, площадь сечения кольца равна dω=2πrdr, а расход жидкости через это сечение равен:

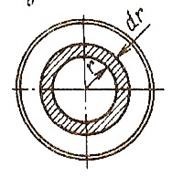dQ=udr= u2πrdr
Подставляя сюда выражение скорости 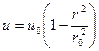и интегрируя, получим:

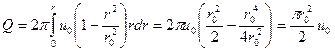, т.е. .

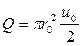Это есть выражение расхода через осевую скорость в трубе.

С другой стороны 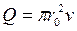, где v-средняя скорость в живом сечении потока.

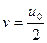=> .Т.о., средняя скорость потока при лам.режиме равна половине осевой.

С учетом этого результата из выражения для потерь напора на трение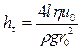

можно получить выражение для потерь напора по длине l в виде: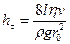

или, введя вместо радиуса диаметр трубы и выражая абсолютную вязкость η через кинематическую (η=v∙ρ), в виде .

Из этой формулы видно, что потери напора при ламинарном движении пропорциональны первой степени средней скорости или расхода жидкости.

Эту формулу можно представить в другом виде, если учесть, что .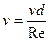

Делая соответствующую подстановку, получим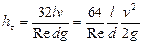

Или, введя обозначение 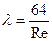, окончательно получим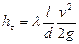

Это универсальная формула Вейсбаха-Дарси,

где λ - коэффициент гидравлического трения или коэф. гидравлического сопротивления.

Формула Дарси-Вейсбаха используется для определения потерь на трение как для ламинарного, так и для турбулентного течения, однако, если для ламинарного движения коэффициент гидравлического сопротивления λ вычисляется по формуле λ=64/Re, то для турбулентного движения формулы будут иметь другой вид.

Формула Пуазейля.

Течение Пуазейля- ламинарное течение жидкости через тонкие цилиндрические трубки. Описывается законом Пуазейля.

Окончательно потери напора при ламинарном движении жидкости в трубе: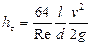

Несколько преобразовав формулу для определения потерь напора, получим формулу Пуазейля: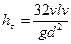

Закон установившегося течения в вязкой несжимаемой жидкости в тонкой цилиндрической трубке круглого сечения. Сформулирован впервые ГоттфильхомХагеном в 1839 и вскоре повторно выведен Ж.Л. Пуазейлем в 1840. Согласно закону, секундный объемный расход жидкости пропорционален перепаду давления на единицу длины трубки. Закон Пуазейля применим только при ламинарном течении и при условии, что длина трубки превышает так называемую длину начального участка необходимую для развития ламинарного течения в трубке.

Свойства течения Пуазейля:

-Течение Пуазейля характеризуется параболическим распределением скорости по радиусу трубки.

-В каждом поперечном сечении трубки средняя скорость вдвое меньше максимальной скорости в этом сечении.

Из формулы Пуазейля видно, что потери напора при ламинарном движении пропорциональны первой степени скорости или расхода жидкости.

Формулой Пуазейля пользуются при расчетах показателей транспортировки жидкостей и газов в трубопроводах различного назначения. Ламинарный режим работы нефте- и газопроводов является наиболее выгодным в энергетическом отношении. Так, в частности, коэффициент трения при ламинарном режиме практически не зависит от шероховатости внутренней поверхности трубы (гладкие трубы).