Относительный покой жидкости.

Понятие относительного покоя. В предшествующем изложе­нии гидростатики предполагалось, что жидкость находится в по­кое относительно некоторой условно неподвижной системы отсчета (в так называемом абсолютном покое). Неподвижными относительно этой системы предполагаются также сосуды, в ко­торых заключена жидкость. При таком предположении и полу­чено основное уравнение гидростатики.

Перейдем к рассмотрению так называемого относительного по­коя жидкости. Под этим определением подразумевается, что части­цы жидкости, заключенной в некотором сосуде, не имеют перемещений друг относительно друга и вся масса жидкости покоит­ся относительно стенок сосуда, следовательно, относительно жестко связанных с сосудом координатных осей, в то же время сосуд пере­мещается произвольным образом относительно неподвижной систе­мы отсчета.

Из основ механики известно, что законы, описывающие абсолют­ный или относительный покой (а также абсолютное или относитель­ное движение), не различаются между собой, если подвижная система отсчета перемещается относительно неподвижной инерциальным образом, т.е. прямолинейно и равномерно. Рассмотрим два примера относительного покоя жидкости.

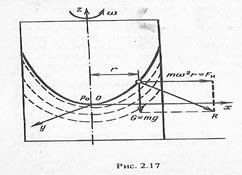
Относительный покой однородной жидкости в цилиндриче­ском сосуде, вращающемся вокруг вертикальной оси. Подвижные координатные оси расположим так, что ось Oz направлена верти­кально вверх (рис. 2.17). Сосуд, благодаря трению, вовлекает в дви­жение наполняющую его жидкость и по истечении небольшого промежутка времени, после начала вращения, жидкость также на­чинает приходить во вращение с той же угловой скоростью, что и сам сосуд. Таким образом, в дальнейшем жидкость покоится относи­тельно сосуда, что позволяет применить уравнения гидростатики, но в координатах, жестко связанных с сосудом, т.е. вращающихся в пространстве.

Приложенными к частицам жидкости массовыми силами являют­ся по-прежнему силы тяжести, параллельные оси z; силами инерции F_и в переносном движении в данном случае являются центробежные силы, перпендикулярные к оси z, имеющие ускорение (ω²r), где r = √(x² + у²) есть расстояние данной частицы жидкости от оси враще­ния. Проекциями ускорения равнодействующей этих сил на оси ко­ординат будут X=│F_и/m│_x= ω²x ; Y=│F_и/m│_y= ω²y ; Z=│F_и/m│_z= ω²z ;

Подставляя эти выражения в (2.8), найдем дифференциальное уравнение поверхностей уровня

ω²(xdx + ydy) – gdz =0. (2.21)

Интегрируя это уравнение, получим ω²/2(x² + y²) – gz =const или ω²r²/2 - gz = const (2.22)

Из (2.22) следует, что поверхности уровня (в том числе и свобод­ная поверхность) являются параболоидами вращения (см. рис. 1.17) вокруг оси z.

Напомним, что распределению давления в несжимаемой жидко­сти соответствует зависимость (2.4).

dp =p(Xdx+Ydy + Zdz),

а в данном случае dp = р [ω² (xdx + ydy) - gdz ],

отсюда (после интегрирова­ния) можно получить

р = р ω²r²/2 - pgz+c. (2.23)

Поместим начало подвиж­ных координат в точку «О» пе­ресечения оси z со свободной поверхностью. Тогда постоян­ная интегрирования опреде­лится из граничного условия р = р₀ при r = 0 и Z= 0. Подста­вив эти значения в (2.23), получим const = р₀, следовательно р = р₀ +р* ω²r²/2 - pgz. (2.24)

Последнее уравнение выражает закон распределения давления в жидкости.

Из уравнения (2.24) видно, что давление в некоторой горизон­тальной плоскости z=const по мере увеличения радиуса увеличива­ется по сравнению с гидростатическим, вычисленным для неподвижного сосуда, на величину p *ω²r²/2 , т.е. тем сильнее, чем больше число оборотов сосуда. Этим пользуются в технике в случа­ях, когда надо увеличить на некоторый период времени давление внутри массы жидкости (увеличение давления, зависящее от значе­ния центробежной силы, лежит также в основе работы центробеж­ных насосов).

Примеры применения основных уравнений гидростатики.

Гидравлика — это наука о законах движения и равновесия жидкостей и способах приложения этих законов к решению конкретных технических задач. С гидравликой связаны отрасли науки и техники, занимающиеся созданием, исследованием и использованием различных гидравлических машин: насосов, турбин, гидропередач и гидропривода. Часто описание теории этих машин, их устройства и принципов работы объединяют в одном учебном предмете «Гидравлика и гидравлические машины».

Слово гидравлика произошло от греческого hydro (вода) и aulos (трубка). В настоящее время это понятие значительно расширилось: гидравлика занимается изучением любой жидкости, движущейся не только в трубах.

Первым научным трудом в области гидравлики принято считать трактат древнегреческого математика и механика Архимеда (ок. 287—212 до н. э.) «О плавающих телах», написанный примерно за 250 лет до н. э. Архимедом открыт закон о равновесии тела, погруженного в жидкость, который затем лег в основу теории плавания кораблей и их остойчивости.

Гидравлические машины предназначены для перемещения жидкостей, преобразования энергии потока жидкости в механическую энергию, а также передачи механической энергии от машины-двигателя к машине-орудию или преобразования различных видов движений и скоростей посредством жидкости. Соответственно гидравлические машины подразделяются на три основных класса: насосы, гидродвигатели и гидропривод. Они различаются по своим энергетическим и конструктивным признакам, но общим для них является то, что в качестве рабочего тела используется жидкость.

Наиболее многочисленный класс гидравлических машин составляют насосы. Всего насчитывается около 130 наименований насосов различных видов. Государственный стандарт определяет насос как машину для создания потока жидкой среды. Этот поток создается в результате силового воздействия вытеснителя на жидкость в рабочей камере насоса. По характеру силового воздействия насосы разделяют на динамические и объемные. К динамическим насосам относятся лопастные, центробежные, осевые, вихревые, струйные, к объемным — поршневые и плунжерные, диафрагменные, крыльчатые, роторные и др.

Гидравлические двигатели, как и насосы, подразделяются на машины динамического и объемного действия. К ним относятся гидравлические турбины, водяные колеса, гидроцилиндры и роторные гидромоторы. Гидродвигатели находят широкое применение в различных областях техники: в гидроэнергетике (гидравлические турбины, которые вырабатывают в стране около 20% электроэнергии) , в нефтедобыче и горном деле (буровые установки, снабженные турбобурами), на транспорте (гидроцилиндры и гидромоторы) и т. д.

Основное уравнение гидростатики : P=P₀+ρgh ;

Используется в гидравлическом прессе.