Ассоциативные и коммутативные операции

Ассоциативной бинарной операцией называется операция φ, если она обладает сочетательным свойством . Ассоциативность позволяет записывать последовательность таких операций без скобок: aj bj c. Ср. в арифметике формулы a + b + c, abcd.

Примером ассоциативных операций служат объединение и пересечение множеств. Операция деления чисел не ассоциативна: (24 : 3) :4 = 2, тогда как 24 : (3 : 4) = 24 : 3/4 = 32. Также не ассоциативно вычитание (проверьте это). Поэтому для бесскобочной записи так называемой алгебраической суммы 20 – 5 –7 принято специальное соглашение: она означает (20 –5) –7, но не 20 – (5 –7), т.е. сложения и вычитания выполняются последовательно слева направо.

Пример. Является ли ассоциативной алгебраическая операция возведения в степень X^Y натуральных чисел, т.е. выполняется ли для всех троек чисел равенство (X^Y)^Z = ?
На примере чисел 5, 3, 2 проверяем: (5³)² = 5⁶ ≠ = 5⁹, следовательно, ассоциативность не выполняется.

Коммутативной бинарной операциейназывается операция, обладающая свойством перестановочности: aj b = bj a.

Пример. Коммутативны сложение и умножение чисел, сложение и скалярное умножение векторов, объединение и пересечение множеств симметрическая разность множеств. Тем же свойством обладает сложение (т.е. последовательное выполнение) поворотов плоскости вокруг начала координат. Некоммутативными операциями над числами являются вычитание и деление
(a – b ≠ b – a, a/b ≠ b/a); некоммутативна разность множеств (A\B ≠ B\A).

Примером некоммутативной операции является сложение S + T (т.е. последовательное выполнение) отражений плоскости относительно любых двух не перпендикулярных друг другу осей; например, оси ординат (операция S) и биссектрисы Y = X (операция T). На рис. 3.1 показано, как точка А (2, 5) переводится преобразованием S в точку А₁(-2, 5), а та, в свою очередь, преобразованием Т – в точку А₂(5, -2). При изменении порядка отражений точка А переходит последовательно в А₃(5, 2) и А₄(-5, 2): А₂≠ А₄.

Рис. 3.1

Упражнение.Определите, для каких пар нижеследующих операций над предметами туалета их последовательное применение перестановочно: "надеть пиджак", "надеть туфли", "надеть шапку", "надеть пальто", "надеть носки".

Ассоциативными и коммутативными являются операции max(X, Y) и min(X, Y) на множестве чисел; поэтому можно употреблять записи без скобок max(X, Y, Z, T), min(A, B, C); к тому же, например, min(A, B, C) = min(В, С, А).

Дистрибутивностьодной бинарной операции φ относительно другой операции ψ выражает распределительный закон, подобный арифметическому соотношению (a + b) · c = a · c + b · c. Свойством дистрибутивности в арифметике обладает умножение относительно сложения, но не обладает сложение относительно умножения: a · (b + c) = a · b + a · c, но a · b + c ≠ (a + c) · (b + c).

Дистрибутивность позволяет раскрывать скобки в формулах.

В операциях над множествами пересечение дистрибутивно относительно объединения:
(А È В) Ç С = (А Ç С) È (В Ç С). Верно и обратное: объединение дистрибутивно относительно пересечения: (А Ç В) È С = (А È С) Ç (В È С).

Изоморфизм двух алгебр сохраняет ассоциативность, коммутативность и дистрибутивность.

Система нескольких алгебраических операций на множестве при возможности их последовательного выполнения в различных сочетаниях образует рассмотренную выше порождающую процедуру. Так, различные вычисления, в том числе достаточно сложные, осуществляются с помощью четырех арифметических действий. Правила шахматной игры определяют возможные ходы, т.е. преобразования позиции на доске, так что разные последовательности ходов создают большое разнообразие шахматных партий.

Двоичная система счисления

1. Хорошо известен способ записи чисел в десятичной системе. Эта система называется позиционной десятичной, потому что натуральное число представляется словом в алфавите из десяти арабских цифр Ц₁₀= [0, 1, 2, 3, ..., 9], причем знаки числа изображают различные его составляющие в зависимости от разряда – позиции в числе и служат коэффициентами при степенях основания – числа 10. Например, 48087 = 40000 + 8000 + 80 + 7 = 4 × 10⁴ + 8 × 10³ +
+ 0 × 10² + 8 ×10¹ + 7 × 10⁰, и цифра 8 во втором разряде изображает число 80, а та же цифра в четвертом разряде – число 8000. Позиционная система исторически вытеснила другие способы представления чисел благодаря удобствам использования, главным образом, из-за достаточно простых алгоритмов арифметических действий над многозначными числами, которые сводятся к действиям над однозначными числами. При этом используются таблица сложения, т.е. правила типа 3 + 6 = 9, 4 + 8 = 12 и т.п., общеизвестная таблица умножения и – при сложении и умножении столбиком – правила переноса десятков в старшие разряды («шестью девять – пятьдесят четыре; четыре пишем, пять в уме»). Отметим, что при сложении столбиком справа налево двух слагаемых каждый очередной знак суммы определяется знаками слагаемых в этом разряде с учетом знака переноса (0, если сумма не превышает 9, или 1, если сумма двузначная). При умножении многозначных чисел A ´ B столбиком каждое умножение A на однозначное число, каким является очередной разряд числа B, также сопровождается переносом числа десятков в следующий разряд. Далее следует сложение нескольких многозначных чисел, записываемых со сдвигом. При сложении большого количества чисел может возникать накопление знаков переноса.

Важно заметить, что как при сложении, так и при умножении каждый знак результата
зависит от знаков слагаемых/сомножителей, находящихся в том же разряде и правее, и не зависит
от старших разрядов (находящихся левее). Так, младший разряд результата является функцией
двух однозначных чисел – младших разрядов слагаемых/сомножителей. Второй справа разряд
есть функция четырех однозначных переменных – знаков двух младших разрядов
слагаемых/сомножителей и т.д.

2. Таким же образом, только много проще, устроена двоичная система счисления. Числа представляются словами в алфавите Ц₂= [0, 1], и например, 110100101₂= 2⁸ + 2⁷ + 2⁵ + 2² + 2⁰ =
= (256 + 128 + 32 + 4 + 1)₁₀= 421₁₀ (подстрочные индексы 2 и 10 обозначают, что одно число записано в двоичной, а другое – в десятичной системе). Вот двоичные представления нескольких первых натуральных чисел (в левом столбце – десятичные; в правом – двоичные):

0 - 0	5 - 101	11 - 1011	16 - 10000
1 - 1	6 - 110	12 - 1100	17 – 10001
2 - 10	7 - 111	13 - 1101	18 - 10010
3 - 11	8 - 1000	14 - 1110	19 – 10011
4 - 100	9 - 1001	15 - 1111	и т.д.

Подобно тому, как в десятичной системе счисления целые степени основания
системы 10 записываются единицей с нулями, а число на 1 меньшее – 99...9, в двоичной системе число 10...0 с k нулями изображает число 2^k (2, 4, 8, 16,...), а число 11...1 из k единиц
равно 2^k – 1 (1, 3, 7, 15,...).

Таблица сложения для двоичных чисел чрезвычайно проста:

0 + 0 = 0; 0 + 1 = 1 + 0 = 1; 1 + 1 = 10.

Таблица умножения еще проще: .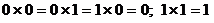

Их можно представить и таблицами с двумя входами:

Отсюда – простота действий над многозначными числами, хотя двоичная запись числа длиннее десятичной более чем втрое. Предыдущий пример демонстрирует перевод двоичного числа в десятичное. Для этого, так же как и для обратного перехода, полезно знать значения шкалы целых степеней числа 2: 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024 и т.д. Каждое целое число можно однозначно представить в виде суммы различных целых степеней числа 2.

Например, 179 = 128 + 51 = 2⁷ + 32 + 19 = = 2⁷ + 2⁵ + 16 + 3 = 2⁷ + 2⁵ + 2⁴ + 2 + 1, поэтому двоичной записью десятичного числа 179₁₀ будет 10110011₂ (слагаемые 2⁷, 2⁵, 2⁴, 2¹, 2⁰ входят в сумму 179 с коэффициентом 1; остальные степени числа 2: 2⁶, 2³, 2² – с коэффициентом 0). Ниже – примеры арифметических действий над двоичными числами (параллельно приведены действия с теми же числами в десятичной записи).

Как видим, сложение, вычитание и умножение многозначных двоичных чисел производится так же, как и десятичных, в частности, в обеих системах k-й знак результата арифметических действий зависит от k-х знаков слагаемых (соответственно, сомножителей) и знаков младших разрядов. Однако накопление знаков переноса при сложении возникает здесь значительно чаще: каждые две единицы дают перенос одной единицы в следующий – старший – разряд, сложение четырех единиц дает две единицы переноса, т.е. перенос одной единицы на два разряда влево.

Деление двоичных чисел «столбиком» также намного проще, чем в десятичной системе, поскольку не приходится подбирать очередной знак частного: остаток не должен быть меньше делителя, – в этом случае знак частного 1; в противном случае, как и для десятичных чисел, он равен 0, и нужно приписать к остатку (снести) очередной разряд делимого.

3. Двоичные числа можно рассматривать и как упорядоченные наборы цифр, или, по-другому, слова в двухбуквенном алфавите В = {0, 1}. При этом иногда добавляют нули слева от значащих цифр, например, чтобы уравнять длину двух таких наборов, и можно было бы считать оба набора векторами многомерного арифметического пространства, а сами двоичные цифры - компонентами этих векторов. Тогда результат арифметических действий над двоичными числами также двоичный вектор, возможно иной (для сложения и умножения – большей) размерности.

Среди алгебраических операций над двоичными векторами можно выделить поразрядные операции, например, поразрядное умножение: k-й знак результата равен произведению k-х знаков сомножителей. Другая операция – поразрядная сумма по модулю 2: k-й знак результата равен остатку от деления на два обычной арифметической суммы k-х знаков слагаемых.

Таблица этой операции для однозначных двоичных чисел a Å b:

Å

Значения a Å b равны 1, если ровно одно из слагаемых равно 1, т.е. если оба слагаемых различны, и равны 0, если оба слагаемых одинаковы.

Если рассматривать двоичный n-мерный вектор 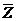как представление характеристической функции χ_M упорядоченного подмножества М n-элементного универсального множества
(k-я компонента вектора равна 1, если k-й элемент универсального множества принадлежит множеству М), то поразрядное произведение 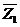• 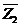двух таких векторов 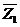и 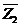представляет характеристическую функцию χ_M∩N пересечения М₁ ∩ М₂ соответствующих множеств М₁ и М₂, равную χ_M • χ_N, а поразрядная сумма по модулю 2 - вектор 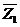Å 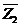- характеристическую функцию χ_MΔNсимметрической разности М₁ Δ М₂ тех же множеств, равную χ_M Å χ_N.

4. Рассмотрим для каждого n (n = 1, 2, 3,...) последовательность D_n всех двоичных наборов длины n в алфавитном порядке, записанную в столбик. На рис. 3.2 - таблицы D₁ , D₂ , D₃.

Рис. 3.2

Если эти наборы из нулей и единиц прочитать как двоичные числа, игнорируя начальные нули, то это будет начальный отрезок натурального ряда от 0 до 2ⁿ-1. Для любого k < 2^n-1 сумма
k-го от начала числа d_k и k-го от конца 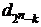равна одному и тому же числу (2ⁿ - 1), которое в двоичной записи состоит из n единиц. При вычитании из двоичного числа (2ⁿ - 1) любого меньшего числа не требуется заимствования единиц из старших разрядов (подобно вычитанию из числа 99...9 в десятичной системе), и единице в вычитаемом соответствует ноль в разности, и наоборот, нулю в вычитаемом отвечает единица в разности. Поэтому двоичные знаки числа d_k противоположны соответствующим знакам числа 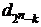. Другими словами, таблица D_n антисимметрична относительно своей середины.

Таблица D_n, строки которой суть наборы из 0 и 1 длины n, может быть построена по индуктивному правилу (рис. 3.3):

1) таблица D₁ – это столбец из двух однозначных чисел 0 и 1;

2) таблица D_k получается из двух экземпляров таблицы D_k-1 (которая состоит из строк длины k-1): к первому из них присоединяется слева столбец из 2^k-1 нулей, а ко второму – столбец
из 2^k-1 единиц. Расположенные одна под другой, обе таблицы образуют таблицу D_k из 2^k строк длины k.

Рис. 3.3

Проценты

Процентом (от лат. “pro cento” - с сотни) некоторой величины называется сотая часть этой величины.

Три основные задачи на проценты таковы.

Задача 1. Найти указанный процент данного числа a.

Для этого данное число умножается на число процентов; результат делится на 100, то есть
р% от числа а составляет х = .

Задача 2. Найти число по заданной величине b и указанному ее проценту p.

Для этого заданная величина делится на число процентов; результат умножается на 100, то есть если р% от х равно b, то х = .

Задача 3. Найти выражение одного числа a в процентах от другого числа b.

Для этого умножаем первое число на 100, результат делим на второе число, то есть а составляет % от b.

Указания. При решении задач на проценты необходимо твердо помнить, что:

1) при нахождении нескольких процентов от числа данное число принимается за 100%;

2) при нахождении числа по данным его процентам искомое число принимается за 100%;

3) при нахождении процентного отношения двух чисел за 100% принимается то число, с которым сравнивается другое.

Пример 1. На товар снизили цену сначала на 15%, а через год еще на 12%. Какова теперь цена товара, если до первого снижения цен он стоил 18000 руб.?

Решение. Уменьшить число на р% - это значит умножить его на (1- ).

В самом деле, из задачи 1 вытекает, что р% от числа а составляет . Значит, после уменьшения числа а на р% получится число а - = а • (1- ). Таким образом, после первого снижения цена товара будет равна 18000 • (1-0,15) = 15300 (руб). После второго снижения цены на 12% новая цена товара равна 15300 • (1-0,12) = 13464 (руб).

Пример 2. Цена на товар понизилась на 40%, затем возросла на 25%. На сколько процентов изменилась цена товара по сравнению с первоначальной ценой?

Решение. Обозначим через а первоначальную цену товара. Тогда после первого снижения цена товара будет равна а • (1-0,4) = 0,6а. После второго изменения новая цена будет равна
0,6а • (1+0,25) = 0,75а. Значит, цена товара после двукратного изменения уменьшилась на величину а – 0,75а = 0,25а, что составляет % = 25% (см. задачу 3).

Пример 3. Первое число составляет 40% от второго. Сколько процентов от первого числа составляет второе?

Решение. Пусть а – первое число. Тогда второе число будет равно = 0,4а (см. задачу 1). Значит, второе число от первого составляет % = 250% (см. задачу 3).

Пример 4. Первое число на 25% больше второго. На сколько процентов второе число меньше первого?

Решение. Второе число обозначим через а. Тогда первое число будет равно
а • (1+0,25) = 1,25а (см. задачу 1). В то же время второе число меньше первого на величину
(1,25а – а) = 0,25а. Как следует из задачи 3, она составляет % = 20%.

При многоэтапном начислении банковских процентов могут применяться две схемы. Схема простых процентов представляет собой процесс, при котором сумма вклада возрастает на каждом этапе на одно и то же количество процентов по отношению к первоначальному значению S₀. При этом она возрастает на одну и ту же величину, т.е. изменяется в арифметической прогрессии с разностью прогрессии d и соотношением S_n+1 = S_n + d.

В схеме сложных процентов величина возрастает на каждом этапе на одно и то же количество процентов по отношению к предыдущему значению S_n, т.е. в одно и то же число раз, и изменяется в геометрической прогрессии со знаменателем прогрессии q и соотношением b_n+1 = b_n • q.

Пример. Если банк начисляет ежегодно 10% на вклад 3000 руб. по схеме простых процентов, то первоначальная сумма будет последовательно принимать значения 3300, 3600, 3900, 4200,... (разность прогрессии равна 300 руб.). По схеме сложных процентов она будет принимать значения 3300, 3630, 3993, 4392.3,... (знаменатель прогрессии равен 1.1).

БИНАРНЫЕ ОТНОШЕНИЯ

Отношения на множествах

1. Одним из синонимов общего понятия соответствия является отношение.

Начнем с примеров. Натуральные числа могут быть полными квадратами, как 4, 81, 144, или не быть ими, как 5, 30, 48. Это свойство, или признак числа, можно трактовать как принадлежность к определенному подмножеству натуральных чисел – полных квадратов
{0, 1, 4, 9, 16, 25,...}. То же можно сказать про признак «X > 2» для действительных чисел: число
5 обладает этим свойством, а число 1 – нет. Напротив, неравенство X > Y выражает свойство не одного числа X или Y, а совокупное свойство пары чисел: если X = 5, Y = 3, то неравенство выполняется, а для пар (5, 10) и (3, 5) не выполняется. Можно выразить это так: условие X > Y выполнено для определенного множества пар чисел.

Некоторые понятия как в математике, так и в обычном языковом употреблении самими своими названиями предполагают отношения между субъектами или объектами: сосед, знакомый (чей-то), одноименный, сопоставимый (с кем-либо или чем-либо), отличающийся (от чего-то другого), внутри, снаружи, между и др.

Таким образом, бинарное отношение – это свойство, присущее некоторым парам элементов
a Î M₁, b Î M₂. Обозначения бинарного отношения R(a, b) или aRb сходны с обозначением алгебраической операции, но результат отношения – выполнение или невыполнение свойства R. Можно также считать, что результат – множество тех пар (a, b), для которых свойство R выполнено.

Примеры: 1) бинарное отношение равенства между двумя числами, фигурами, множествами;

2) бинарное отношение старшинства между людьми по возрасту («старше», «моложе») или воинскому званию;

3) бинарные родственные и другие отношения между людьми: «быть отцом», «быть внуком», «быть одноклассниками», «быть одногодками»;

4) бинарное отношение C₇ между целыми числами – «иметь одинаковые остатки от деления на 7»;

5) отношение принадлежности элемента a множеству M, выполненное для всех таких пар
(a, M), что a Î M;

6) бинарное отношение инцидентности точки и прямой на плоскости или в пространстве: точка А лежит на прямой l.

Упражнение. 1) Определите, находятся ли в отношении C₇пары чисел: (12, 26), (16, 34), (34, 16), (26, 12);

2) в каком отношении из примера 2 находятся Л.Н. Толстой и И.С. Тургенев?

3) находятся ли в отношении инцидентности точка плоскости (4, 1) и прямая Y = X – 3?

Поскольку бинарные отношения являются множествами, то к ним применимы все теоретико-множественные операции: объединение, пересечение, дополнение и др. Так, объединение отношений X > Y и X = Y на числовом множестве есть отношение X ³ Y , а дополнение к последнему есть отношение X < Y.

Еще один важный пример – отношение включения для множеств. Если M, N – подмножества универсального множества U , то (M Í N) – бинарное отношение M есть подмножество множества N;например, как указано выше, для чисел выполнено включение Z Í R.

2. Равенство отношений R₁= R₂ есть равенство множеств R₁ и R₂, определяющих эти отношения, хотя бы они были выражены по-разному. Например, отношения между натуральными числами «иметь одинаковые остатки от деления на 2» и «давать при сложении четное число» совпадают. Действительно, остатки от деления двух чисел p и q на 2 равны, если они оба четные
(в этом случае остаток 0) или оба нечетные (остаток 1).

То же при сложении чисел p и q: если сумма четная, то оба слагаемых – одной четности, в то время как сумма четного и нечетного чисел – нечетна.

Бинарное отношение на конечном множестве можно представить квадратной матрицей (таблицей), у которой строки и столбцы – это элементы множества, а элемент матрицы, находящийся на пересечении строки x и столбца y, равен 1, если xRy, и равен 0 в противном случае.

Пример. Рассмотрим 4 отношения R₁, R₂, R₃, R₄ на множестве из трех элементов M{a, b, c}; каждое из них задано перечислением пар, для которых это отношение выполнено.

R₁= {(a, b), (b, c), (c, a)};

R₂ = {(a, a), (a, b), (b, b), (b, c), (c, a)};

R₃= {(a, a), (a, b), (b, b), (c, c)};

R₄= {(a, a), (a, b), (a, c), (b, a), (b, c), (c, a), (c, b)}.

Соответствующие матрицы:

, , , .

Бинарное отношение aRb можно изобразить схемой (рис. 4.1) сопоставив элементам множества точки (вершины), а парам (a, b) R-связки (линии со стрелками, идущие из a в b).

Рис. 4.1

Инверсией бинарного отношения R называется отношение, обозначаемое R^-1 и такое, что aR^-1b тогда и только тогда, когда bRa. Понятно, что инверсией отношения R^-1 является отно-шение R, т.е. можно сказать, что отношения R и R^-1 взаимно обратны.

Пример. Инверсией для отношения «больше» является отношение «меньше»; то же – для их разновидностей: «старше – моложе», «дороже – дешевле», «выше – ниже» и т.п.; инверсия отношения «x – внук y» - «y – дед x».

Инверсия отношения отличается от отрицания: инверсией отношения x > y на множестве чисел является отношение x < y, тогда как отрицанием – отношение x ≤ y.

Инверсия отношения инцидентности точки и прямой – прямая l проходит через точку А.

3. Возможно обобщение понятия бинарного отношения: n-арное (n-местное) отношение на множестве М - подмножество R Í Mⁿ; обозначение - R(m₁, m₂,..., m_n). Говорят, что элементы, составляющие принадлежащий множеству R набор (m₁, m₂,..., m_n), находятся в n-арном отношении R, причем это свойство не отдельных элементов, а именно их совокупности. Полезно рассматривать и одноместное (унарное) отношение – его можно называть признаком,
или свойством элементов множества. В более общем смысле n-арное отношение можно определить и для совокупностей элементов различных множеств M₁, M₂,..., M_n как подмножество R Í M₁ ´ M₂ ´ . . . ´ M_n. Число n называется арностью, или местностью отношения.

Примеры. 1) Трехместное (тернарное) отношение «между» для тройки точек А, В, С на прямой: точка В расположена между точками А и С.

2) Тернарное отношение для тройки точек на плоскости – «лежать на одной прямой».

3) Четырехместное отношение для точек пространства – «принадлежать одной плоскости» (можно заметить, что трехместное отношение для точек пространства – «принадлежать одной плоскости» выполнено для любых трех точек).

4) Четырехместное отношение для четверки чисел X, Y, Z, T – «быть пропорциональными», т.е. удовлетворять соотношению X/Y = Z/T.

5) Тернарное отношение S(А, В, l) двух точек А, В и прямой l на плоскости – «точки А и В находятся по разные стороны от прямой l».