Изображение синусоидальной функции комплексным числом. Символический метод расчета цепей синусоидального тока.
Метод расчета цепей синусоидального тока, основанный на изображении гармонических функций времени комплексными числами, называется символическим методом. Сущность символического метода состоит в том, чтобы, используя комплексные числа, перейти от составления и решения интегро-дифференциальных уравнений для мгновенных значений токов и напряжений к составлению и решению алгебраических уравнений для функций оператора комплексной плоскости.
В курсе электротехники используются следующие формы записи комплексного числа:
а) алгебраическая 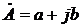 ;
;
б) показательная 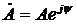 ;
;
в) тригонометрическая 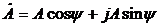 .
.
Здесь 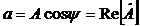 – действительная часть комплексного числа
– действительная часть комплексного числа 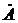 ;
; 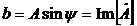 – мнимая часть комплексного числа
– мнимая часть комплексного числа 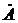 ;
; 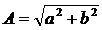 – модуль комплексного числа
– модуль комплексного числа 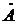 ;
; 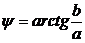 – аргумент комплексного числа
– аргумент комплексного числа 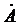 ;
; 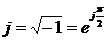 – мнимая единица или оператор поворота на угол p/2=900 (умножение на +j сводится к повороту вектора против часовой стрелки на угол 900, а умножение на
– мнимая единица или оператор поворота на угол p/2=900 (умножение на +j сводится к повороту вектора против часовой стрелки на угол 900, а умножение на 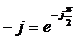 – к повороту вектора на угол 900 по часовой стрелке).
– к повороту вектора на угол 900 по часовой стрелке).
Комплексное число изображается в системе координат (+1; +j) следующим образом (рис. 2.3):
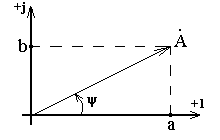
Рис. 2.3. Изображение комплексного числа на комплексной плоскости
Действия над комплексными числами.
а) С использованием алгебраической формы записи комплексного числа (пусть 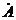 =(a1+jb1),
=(a1+jb1), 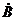 =(a2+jb2)):
=(a2+jb2)):
- сложение: 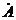 +
+ 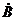 =(a1+jb1)+(a2+jb2)=(a1+a2)+j(b1+b2)=
=(a1+jb1)+(a2+jb2)=(a1+a2)+j(b1+b2)= 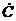 ;
;
- умножение: 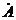 ×
× 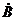 =(a1+jb1)×(a2 +jb2)=(a1a2–b1b2)+j(a1b2+a2b1)=
=(a1+jb1)×(a2 +jb2)=(a1a2–b1b2)+j(a1b2+a2b1)= 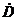 ;
;
- деление: 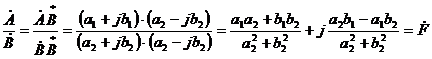 ,
,
где число 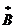 – комплексно-сопряженное числу
– комплексно-сопряженное числу 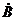 (отличаются знаком мнимой части). Произведение комплексно-сопряженных чисел – действительное число, равное квадрату их модуля:
(отличаются знаком мнимой части). Произведение комплексно-сопряженных чисел – действительное число, равное квадрату их модуля: 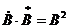 .
.
б) С использованием показательной формы комплексного числа (пусть 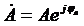 ,
, 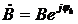 ): в этом случае удобнее производить операции умножения, деления, возведения в степень, чем в случае использования алгебраической формы.
): в этом случае удобнее производить операции умножения, деления, возведения в степень, чем в случае использования алгебраической формы.
- умножение: 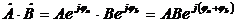 ;
;
- деление : 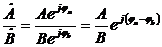 ;
;
- возведение в степень: 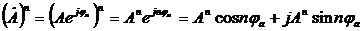 ;
;
- извлечение корня: 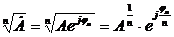 .
.
Различные формы записи комплексного числа объединяются между собой при помощи формулы Эйлера:
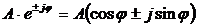 .
.
Мгновенное значение синусоидальной функции есть мнимая часть изображающей ее комплексной амплитуды, умноженной на e+jwt:
a(t)=Im[ 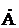 mejwt]=Im[Amej(wt + j)]=Amsin(wt+j).
mejwt]=Im[Amej(wt + j)]=Amsin(wt+j).
Комплексные выражения синусоидальной функции времени, ее производной и интеграла представлены в таблице 2.1.
Таблица 2.1
| Временная и комплексная записи | Функция | Производная функции | Интеграл от функции |
| Запись во временной области | a=Amsin(wt+y) | 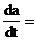 wAmcos(wt+y) wAmcos(wt+y) | 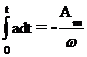 cos(wt+ y) cos(wt+ y) |
| Комплексная функция времени | Amej×(wt + y ) | wAmej×(wt + y + p / 2) | 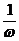 ×Amej×(wt +y - p /2) ×Amej×(wt +y - p /2) |
| Комплексная амплитуда | 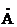 m = A m ejy m = A m ejy | jw 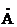 m m | 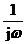 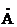 m m |
| Комплексное действующее значение | 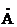 = A m ejy = A m ejy | jw 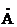 | 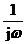 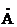 |
Например, для тока i, падения напряжения на активном сопротивлении uR, индуктивности uL и емкости uC соответствующие комплексные амплитуды записываются следующим образом:
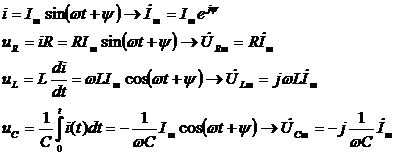
(здесь стрелка ® означает знак соответствия).
