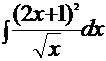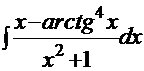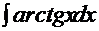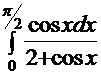Тема 1.5. Аналитическая геометрия
32. Понятие уравнения геометрического образа.
33. Плоскость, нормальный вектор плоскости. Общее уравнение плоскости и его частные случаи.
34. Угол между плоскостями, условие перпендикулярности и параллельности плоскостей, расстояние от точки до плоскости. Плоскость в Еn, n>3.
35. Прямая в Е3, ее направляющий вектор. Общие, канонические, параметрические уравнения прямой. Луч и отрезок.
36. Угол между прямыми в Е3. Перпендикулярные, параллельные, пересекающиеся и скрещивающиеся прямые. Расстояние от точки до прямой в Е3. Прямая, луч и отрезок в Еn, n>3.
37. Угол между прямой и плоскостью, условия параллельности и перпендикулярности прямой и плоскости. Точка пересечения прямой и плоскости, принадлежность прямой плоскости.
38. Прямая на плоскости, как частный случай прямой в Е3 и как линия пересечения плоскости с плоскостью ОХУ.
39. Уравнение прямой на плоскости с угловым коэффициентом.
40. Уравнение кривой второго порядка, его преобразование с помощью поворота и параллельного переноса осей координат.
41. Эллипс, гипербола, парабола. Оси симметрии, центр, вершины, эксцентриситет. Канонические уравнения и уравнения со смещенным центром.
Раздел 2. Математический анализ
Темы 2.1-2.5.
42. Множество, операции с множествами.
43. Функция одной переменной, способы задания. Основные элементарные функции, их графики. Сложная функция.
44. Предел функции при х®х0 (х®¥).
45. Бесконечно малая функция и ее свойства.
46. Бесконечно большая функция, связь с бесконечно малой.
47. Основные теоремы о пределах функции (критерий существования предела, единственность, предел суммы, произведения, частного).
48. Первый и второй специальные пределы.
49. Сравнение бесконечно малых функций.
50. Односторонние пределы функции.
51. Непрерывность функции в точке, на интервале, отрезке. Точки разрыва и их классификация.
52. Основные теоремы о непрерывных функциях (непрерывность основных элементарных функций, сложной функции).
53. Свойства функций непрерывных на замкнутом отрезке, абсолютный экстремум функции.
Тема 2.6. Дифференциальное исчисление функции одной переменной
54. Приращение аргумента и приращение функции. Задача о касательной к плоской кривой.
55. Производная функции, ее геометрический и физический смысл. Уравнение касательной и нормали к кривой.
56. Темп роста и эластичность функции.
57. Необходимое условие дифференцируемости функции.
58. Основные правила и формулы дифференцирования.
59. Дифференциал функции, его геометрический смысл, свойства, применение к приближенным вычислениям.
60. Производные и дифференциалы высших порядков.
Семестр
Тема 2.7. Неопределенный интеграл (НИ)
1.Первообразная. Теорема о первообразной. НИ, его геометрический смысл.
2. Свойства НИ.
3. Теорема о замене переменной в НИ.
4. Таблица основных интегралов.
5. Интегрирование по частям в НИ.
6. Рациональные дроби, правильные и неправильные дроби. Интегрирование неправильных дробей (теорема).
7. Простейшие рациональные дроби, их интегрирование. Теорема о разложении правильной дроби на сумму простейших дробей.
8. Интегрирование тригонометрических функций.
9. Интегрирование простейших иррациональностей.
10. Тригонометрические подстановки.
Тема 2.8. Определенный интеграл (ОИ)
11. Задача о вычислении площади криволинейной трапеции.
12.ОИ как предел интегральных сумм. Геометрический смысл ОИ. Теорема существования ОИ.
13. Свойства ОИ, теорема о среднем.
14 Теорема о производной от интеграла с переменным верхним пределом.
15. Формула Ньютона-Лейбница (теорема).
16. Замена переменной и интегрирование по частям в ОИ.
17. Теоремы о площади плоской фигуры, ограниченной линиями, заданными а) в декартовой системе координат; б) параметрически.
18. Длина дуги плоской кривой. Теорема о длине дуги в декартовой системе координат и ее следствия.
19. Вычисление объемов тел по площадям поперечных сечений (теорема). Объем тела вращения.
20. Экономические приложения ОИ.
21. Несобственные интегралы 1-го рода и 2-го, их определение, вычисление и геометрический смысл.
Раздел 3. Дифференциальные уравнения
Темы 3.1, 3.2
22. Дифференциальные уравнения первого порядка. Основные понятия
23. ДУ с разделяющимися переменными
24. Однородные ДУ.
25. Линейные дифференциальные уравнения.
26. Дифференциальные уравнения второго порядка. Основные понятия
27.Линейные дифференциальные уравнения второго порядка
Раздел 3. Ряды
Темы 4.1-4.3
28. Числовые ряды. Частичная сумма. Сумма ряда
29. Необходимый признак сходимости. Гармонический ряд
30. Достаточные признаки сходимости. Признак сравнения
31. Признак Даламбера
32. Радикальный признак Коши
33. Интегральный признак Коши
34. Знакочередующиеся ряды. Признак Лейбница
Функциональные ряды. Сходимость функциональных рядов
Задания для промежуточной аттестации
Вариант №1
-----------------------------------------------------------------------------------------------------------------------------------
1. Определитель 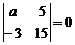 при значении а равном… Варианты ответов: а) -1; б) 5; в) -5; г) 1.
при значении а равном… Варианты ответов: а) -1; б) 5; в) -5; г) 1.
2. Матрица D=AB, где 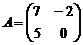 ,
, 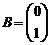 равна… Варианты ответов: а)
равна… Варианты ответов: а)  ; б)
; б) 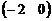 ; в)
; в) 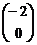 ; г)
; г)  .
.
3. Диагональной матрицей называется…
Варианты ответов:
а) матрица, все элементы которой, стоящие ниже главной диагонали, равны нулю;
б) матрица, все элементы которой, не стоящие на главной диагонали, равны нулю;
в) матрица, полученная из данной матрицы заменой каждой ее строки столбцом с тем же номером;
г) матрица, все элементы которой стоящие на главной диагонали равны единице, а остальные элементы равны нулю.
4. Решением системы 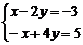 является…
является…
Варианты ответов: а) x = 0, y = 1; б) x = -1, y = 1; в) x = -2, y = 1; г) x = 0, y = 0.
-----------------------------------------------------------------------------------------------------------------------------------
5. Прямая проходит через точки А(2,-1) и В(3,1). Тогда ее угловой коэффициент равен…
Варианты ответов: а) 2; б) 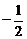 ; в) -2; г)
; в) -2; г) 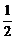 .
.
6. Уравнением прямой, параллельной 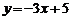 , является …
, является …
Варианты ответов: а) 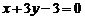 ; б)
; б) 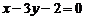 ; в)
; в) 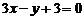 ; г)
; г) 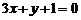
7. Уравнение гиперболы имеет вид 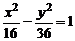 . Длина ее мнимой полуоси равна…
. Длина ее мнимой полуоси равна…
Варианты ответов: а) 16; б) 4; в) 6; г) 36.
8. Координаты нормального вектора плоскости 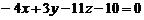 равны…
равны…
Варианты ответов: а) {-4, 3, -11}; б) {-4, -11, -10}; в) {3, -11, -10}; г) {-4, 3, -10}.
9. Прямая 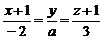 параллельна плоскости
параллельна плоскости 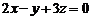 при значении а равном…
при значении а равном…
Варианты ответов: а) 1; б) 0; в) 5; г) -5.
10. Уравнение прямой проходящей через точку N (0,-3,1) перпендикулярно плоскости 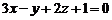 имеет вид…
имеет вид…
Варианты ответов: а) 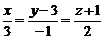 ; б)
; б) 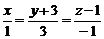 ; в)
; в) 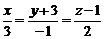 ; г)
; г) 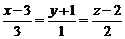 .
.
11. Расстояние от точки А (1,-7,-3) до плоскости 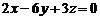 равно…
равно…
Варианты ответов: а) 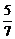 ; б) 49; в) 5; г) 7.
; б) 49; в) 5; г) 7.
12. Установить какая из точек А (1,1,1), В (1,-2,0), С (0,1,0), D (0,-3,1) принадлежит плоскости 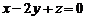
Варианты ответов: а) А; б) B; в) C; г) D.
13. Скалярное произведение векторов 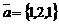 и
и 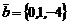 равно…
равно…
Варианты ответов: а) 2; б) 1; в) -8; г) -2.
14. Даны векторы 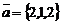 и
и 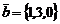 , тогда их векторное произведение имеет вид…
, тогда их векторное произведение имеет вид…
Варианты ответов: а) 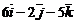 ; б)
; б) 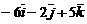 ; в)
; в) 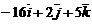 ; г)
; г) 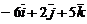
15. Смешанное произведение векторов 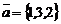 ,
, 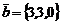 ,
, 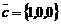 равно…
равно…
Варианты ответов: а) 6; б) 1; в) 0; г) -6.
16. Для вектора 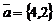 соответствующий ему нормированный вектор имеет вид…
соответствующий ему нормированный вектор имеет вид…
Варианты ответов: а) 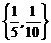 ; б)
; б) 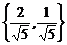 ; в)
; в) 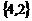 ; г)
; г) 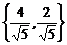 .
.
Примеры заданий по Математическому анализу.
1.Вычислить пределы:
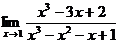
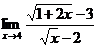
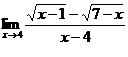
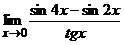
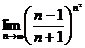
2.Найти производную:
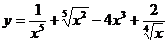
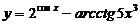
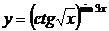
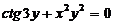
3.Вычислить предел функции, используя правило Лопиталя:
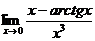
4.Провести полное исследование функции и построить её график:
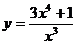
5.Вычислить неопределенный интеграл: