Шкала отношений (степени значимости действий)

Степень значимости	Определение	Объяснение
	Одинаковая значимость	Два действия вносят одинаковый вклад в достижение цели
	Некоторое преобладание значимости одного действия над другим (слабая значимость)	Существуют соображения в пользу предпочтения одного из действий, однако эти соображения недостаточно убедительны
	Существенная или сильная значимость	Имеются надежные данные или логические суждения для того, чтобы показать предпочтительность одного из действий
	Очевидная или очень сильная значимость	Убедительное свидетельство в пользу одного действия перед другим
	Абсолютная значимость	Свидетельства в пользу предпочтения одного действия другому в высшей степени убедительны
2,4,6,8	Промежуточные значения между двумя соседними суждениями	Ситуация, когда необходимо компромиссное решение
Обратные величины приведен-ных выше ненулевых величин	Если действию i при сравнении с действием j приписывается одно из определенных выше ненулевых чисел, то действию j при сравнении с действием i приписывается обратное значение	Если согласованность была постулирована при получении N числовых значений для образования матрицы

Правомочность этой шкалы доказана теоретически при сравнении со многими другими шкалами [2]. При использовании указанной шкалы ЛПР, сравнивая два объекта в смысле достижения цели, расположенной на вышележащем уровне иерархии, должен поставить в соответствие этому сравнению число в интервале от 1 до 9 или обратное значение чисел. В тех случаях, когда трудно различить столько промежуточных градаций от абсолютного до слабого предпочтения или этого не требуется в конкретной задаче, может использоваться шкала с меньшим числом градаций. В пределе шкала имеет две оценки: 1 — объекты равнозначны; 2 — предпочтение одного объекта над другим.

Матрицы парных сравнений

После построения иерархии устанавливается метод сравнения ее элементов. Если принимается метод попарного сравнения, то строится множество матриц парных сравнений. Для этого в иерархии выделяют элементы двух типов: элементы-«родители» и элементы-«потомки». Элементы-«потомки» воздействуют на соответствующие элементы вышестоящего уровня иерархии, являющиеся по отношению к первым элементами-«родителями». Матрицы парных сравнений строятся для всех элементов-«потомков», относящихся к соответствующему элементу-«родителю». Элементами-«родителями» могут являться элементы, принадлежащие любому иерархическому уровню, кроме последнего, на котором расположены, как правило, альтернативы. Парные сравнения проводятся в терминах доминирования одного элемента над другим. Полученные суждения выражаются в целых числах с учетом девятибалльной шкалы (см. табл. 2.1).

Заполнение квадратных матриц парных сравнений осуществляется по следующему правилу. Если элемент E₁ доминирует над элементом Е₂, то клетка матрицы, соответствующая строке Е₁ и столбцу E₂, заполняется целым числом, а клетка, соответствующая строке E₂ и столбцу Е₁, заполняется обратным к нему числом. Если элемент Е₂ доминирует над Е₁, то целое число ставится в клетку, соответствующую строке Е₂ и столбцу Е₁, а дробь проставляется в клетку, соответствующую строке Е₁ и столбцу Е₂. Если элементы Е₁ и Е₂ равнопредпочтительны, то в обе позиции матрицы ставятся единицы.

Для получения каждой матрицы эксперт или ЛПР выносит n(n – 1)/2 суждений (здесь п — порядок матрицы парных сравнений).

Рассмотрим в общем виде пример формирования матрицы парных сравнений.

Пусть Е₁,E₂, ..., Е_п — множество из п элементов (альтернатив) и v₁, v₂, …, v_n — соответственно их веса, или интенсивности. Сравним попарно вес, или интенсивность, каждого элемента с весом, или интенсивностью, любого другого элемента множества по отношению к общему для них свойству или цели (по отношению к элементу-«родителю»). В этом случае матрица парных сравнений [Е] имеет следующий вид:

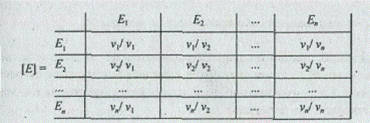
Матрица парных сравнений обладает свойством обратной симметрии, т. е.

a_ij=1/a_ji,

где a_ij=v_i / v_j

При проведении попарных сравнений следует отвечать на следующие вопросы: какой из двух сравниваемых элементов важнее или имеет большее воздействие, какой более вероятен и какой предпочтительнее.

При сравнении критериев обычно спрашивают, какой из критериев более важен; при сравнении альтернатив по отношению к критерию — какая из альтернатив более предпочтительна или более вероятна.