Логические операции, равносильность формул
Цель работы. Изучить логические операции и основные равносильности алгебры логики, научиться составлять таблицы истинности для формул алгебры логики и преобразовывать формулы, используя основные равносильности и правила поглощения.
Рассмотрим следующие операции: отрицание, конъюнкцию, дизъюнкцию, импликацию и эквиваленцию.
Элементарные высказывания обозначаются прописными буквами латинского алфавита: А, В, С... X, Y, Z.
А= «Иванов разбил окно»,
В= «Петров разбил окно».
Задание 1
Постройте таблицы истинности для высказываний
1) 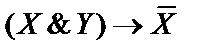 ;
;
2) 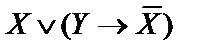 ;
;
3) 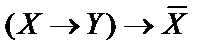 ;
;
4) 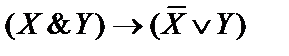 ;
;
5) 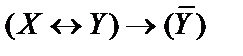 ;
;
6) 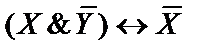 ;
;
7) 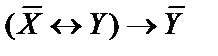 ;
;
8) 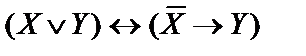 ;
;
9) 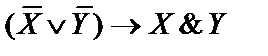 ;
;
10) 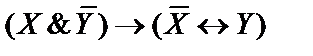 .
.
Методические указания.
Отрицание
Логическая операция, соответствующая логической связке «не» («Неверно, что») называется отрицанием. В результате этой операции получается высказывание ложное, если исходное высказывание истинно, и истинное, если исходное высказывание ложно.
| Х | 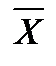 |
Отрицание высказывания Xобозначается 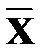 .
.
Конъюнкция
Логическая операция, соответствующая союзу «и» (или близким по смыслу союзам «а» и «но»), называется конъюнкцией.В результате конъюнкции получается высказывание, истинное тогда и только тогда, когда оба элементарных высказывания Xи Yистинны.
Используются обозначения: XÙY, X&Y.
| X | Y | XÙY |
Дизъюнкция
Логическая операция, соответствующая союзу «или», называется дизъюнкцией.В результате этой операции образуется высказывание, ложное тогда и только тогда, когда оба составных высказывания ложны. Дизъюнкция обозначается XÚY.
| X | Y | XÚ Y |
Импликация
Логическая операция, имеющая вид «если X, то Y», называется импликацией.Высказывание Xименуется посылкой (или антецедентом – предшествующим по-латыни), Y – заключением (или консеквентом – последующим). В результате импликации получается высказывание, ложное тогда и только тогда, когда посылка истинна, а заключение ложно. Обозначается импликация X ® Y
| X | Y | X®Y |
Эквиваленция
Логическая операция, соответствующая сложному союзу «тогда и только тогда, когда», «в том и только в том случае», «если и только если», называется эквиваленцией. Врезультате этой операции образуется высказывание, истинное тогда и только тогда, когда оба составляющих его элементарных высказывания истинны или оба ложны.
Эквиваленция обозначается X«Y.
| X | Y | X«Y |
Приоритеты логических операций:
1. отрицание
2. конъюнкция
3. дизъюнкция
4. импликация
5. эквиваленция.
Это позволяет упрощать запись, избавляясь от лишних скобок.
Пример
Построить таблицу истинности для высказывания 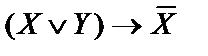 .
.
| X | Y | 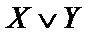 | 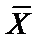 | 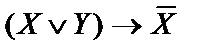 |
Задание 2
Используя основные равносильности алгебры логики, докажите равносильность формул:
1) 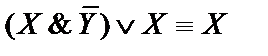 ;
;
2) 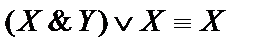 ;
;
3) 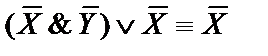 ;
;
4) 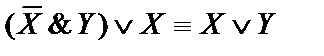 ;
;
5) 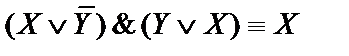 ;
;
6) 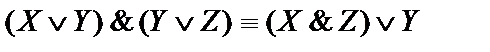 .
.
Методические указания
Основные равносильности алгебры логики
| № | Дизъюнкция | Конъюнкция | |
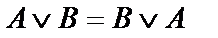 | 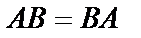 | Коммутативные | |
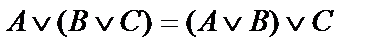 | 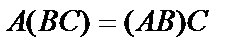 | Ассоциативные | |
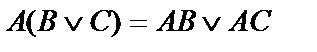 | 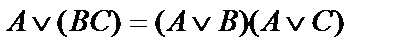 | Дистрибутивные | |
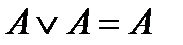 | 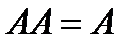 | Идемпотентные | |
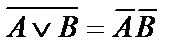 | 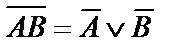 | Законы де Моргана | |
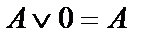 | 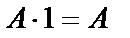 | Законы действий с 0 и 1 | |
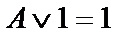 | 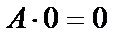 | ||
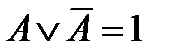 | 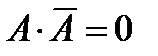 | ||
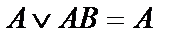 | 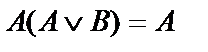 | Законы поглощения | |
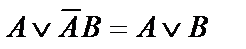 | 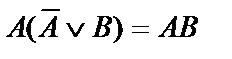 |
Равносильности для импликации и эквиваленции, закон двойного отрицания
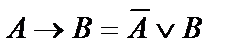 | ||
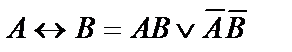 | ||
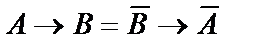 | Закон конрапозиции | |
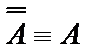 |
Пример
Доказать, что 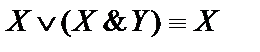 .
.
Решение
Закон единицы для конъюнкции позволяет заменить X на X&1:
X  (X&Y)
(X&Y) 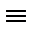 (X&1)
(X&1)  (X&Y).
(X&Y).
Используя дистрибутивный закон, вынесем Xзаскобки:
X  (X&Y)
(X&Y) 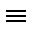 (X&1)
(X&1)  (X&Y)
(X&Y) 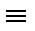 X&(1
X&(1  Y).
Y).
Закон единицы для дизъюнкции гласит 1  Y
Y 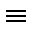 1, а закон единицы для дизъюнкции X&1
1, а закон единицы для дизъюнкции X&1 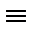 X позволяет получить искомое выражение:
X позволяет получить искомое выражение:
X  (X&Y)
(X&Y) 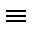 (X&1)
(X&1)  (X&Y)
(X&Y) 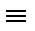 X&(1
X&(1  Y)
Y) 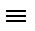 X&1
X&1 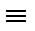 X, что требовалось доказать.
X, что требовалось доказать.
Задание 3
Используя основные равносильности алгебры логики, а также равносильности, упростите формулы:
1) 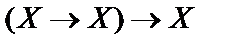 ;
;
2) 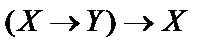 ;
;
3) 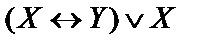 ;
;
4) 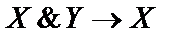 ;
;
5) 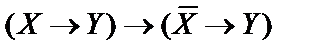 ;
;
6) 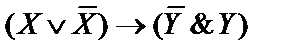 ;
;
7) 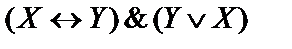 ;
;
8) 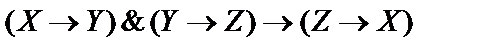 ;
;
9) 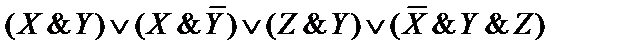 .
.
Методические указания.
Пример.
Используя основные равносильности алгебры логики, а также равносильности 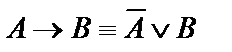 и
и 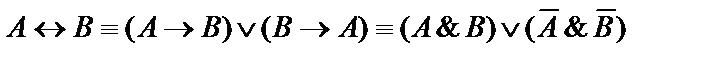 , упростить формулу
, упростить формулу 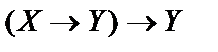 .
.
Решение
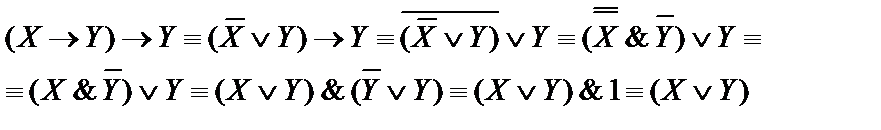
Ответ: 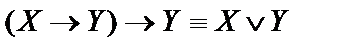
Задание 4 (обобщающее)
Методические указания
Логическую операцию «конъюнкция» в формулах алгебры логики можно опускать, т.е. выражение А&В можно записывать в виде АВ.
Пример.Для заданного высказывания 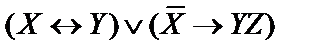 .
.
1) построить таблицу истинности;
2) упростить высказывание, используя равносильные преобразования;
3) полученный результат проверить, построив для него таблицу истинности.
Решение.
1) Таблица истинности:
Пусть 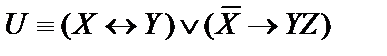
| X | Y | Z | 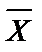 | 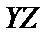 | 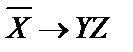 | 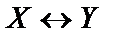 | U |
2) Выполнить равносильные преобразования, используя 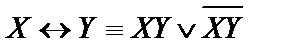 и
и 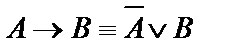 , имеем:
, имеем:
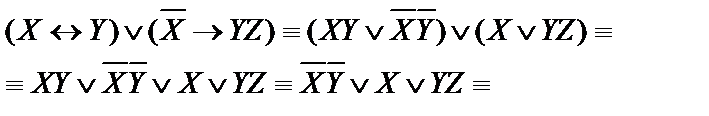
(в последнем преобразовании для первого и третьего слагаемых использовали правило поглощения 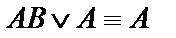 (1), далее использовать другое правило поглощения
(1), далее использовать другое правило поглощения 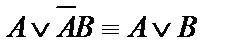 (2), получили)
(2), получили)
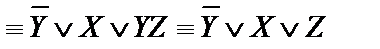 .
.
Еще раз использовали правило поглощения (2).
3) Для полученного выражения построить таблицу истинности:
| X | Y | Z | 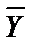 | 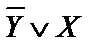 | 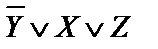 |
Результирующие (последние) столбцы в двух таблицах совпали, следовательно, выполненные преобразования верны.
Задания для самостоятельной работы
Для заданного логического выражения (высказывания):
1) построить таблицу истинности;
2) упростить высказывание, используя равносильные преобразования;
3) полученный результат проверить, построив для него таблицу истинности.
| Вариант | Вариант | ||
| 1. | 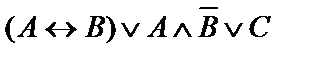 | 2. | 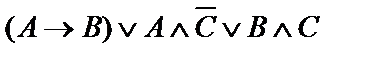 |
| 3. | 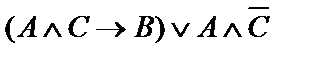 | 4. | 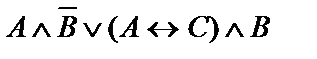 |
| 5. | 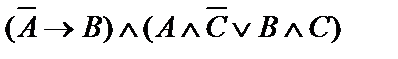 | 6. | 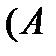 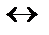 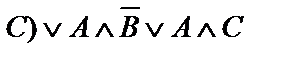 |
| 7. | 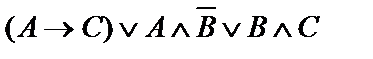 | 8. | 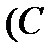 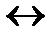 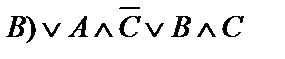 |
| 9. | 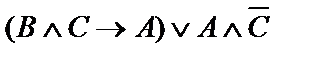 | 10. | 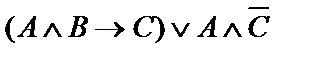 |
| 11. | 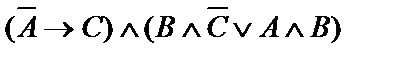 | 12. | 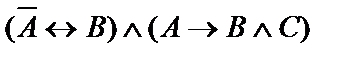 |
| 13. | 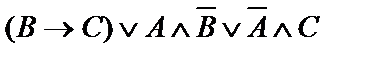 | 14. | 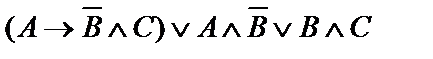 |
| 15. | 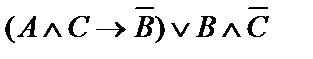 | 16. | 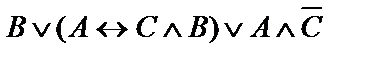 |
| 17. | 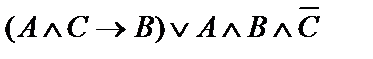 | 18. | 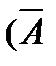 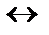 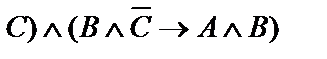 |
| 19. | 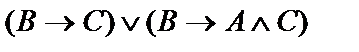 | 20. | 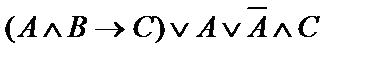 |
| 21. | 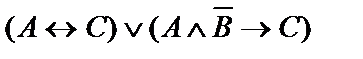 | 22. | 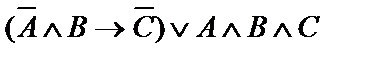 |
| 23. | 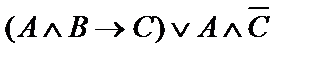 | 24. | 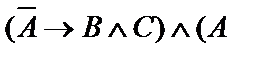 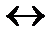  |
| 25. | 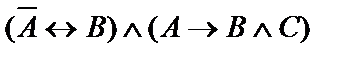 | 26. | 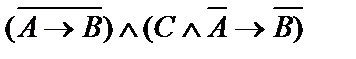 |
Лабораторная работа №7
Приложения алгебры логики
Цель работы. Изучить приложения алгебры логики к построению электронных схем и решению логических задач.
Логические элементы на комбинационных схемах имеют обозначения:
Отрицание
Дизъюнкция
Конъюнкция
Например, схеме соответствует формула a&b&c, или abc, в которой символ конъюнкции опущен.
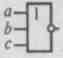 |
 |
А схема реализует формулу 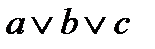
Задание 1
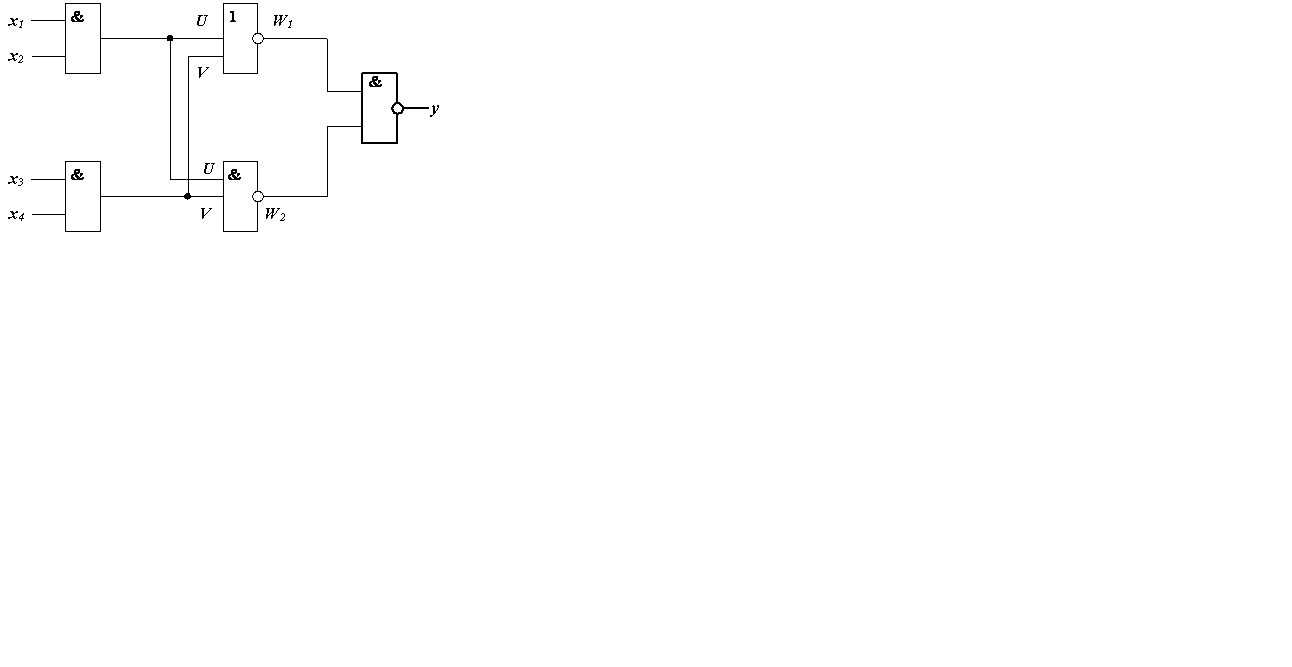
Для заданной комбинационной схемы построить аналитическое выражение и, если возможно, равносильную ей упрощенную схему.
Здесь U=x1  x2, V=x3
x2, V=x3  x4,
x4,
 |
 |
 |
 |
 |
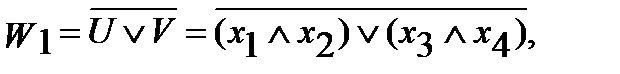
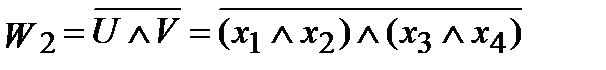 ,
,
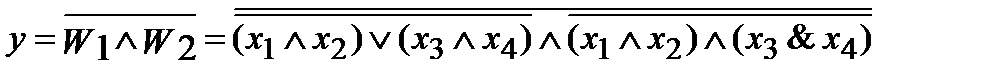 .
.
Преобразуем последнее выражение по закону де Моргана. Получаем 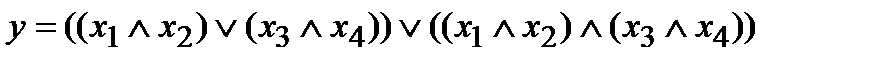 .
.
Используя законы ассоциативности и правила приоритета логических операций, получаем  . Осталось воспользоваться правилом поглощения
. Осталось воспользоваться правилом поглощения 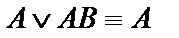 , в результате получим упрощенную формулу, равносильную данной
, в результате получим упрощенную формулу, равносильную данной 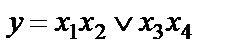 .
.
Ей соответствует упрощенная комбинационная схема
Задание 2
Для заданной логической таблицы функции y(a,b,c) записать аналитическое выражение и построить комбинационную схему.
| a | b | c | y |
Рассмотрим строки таблицы, в которых функция принимает значение 1. На базе этих строк построим элементарные конъюнкции по следующему правилу: единицу заменим именем аргумента, а нуль – именем аргумента с отрицанием. Полученные таким образом элементарные конъюнкции соединим знаками дизъюнкции. Для рассматриваемого примера имеем
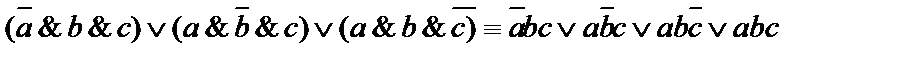 .
.
Объединим первое и четвертое слагаемые и вынесем за скобки bc, получаем 
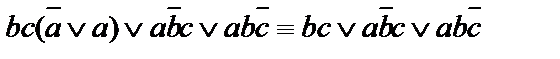 . Объединим первое и второе слагаемые, вынесем за скобки с, а к выражению в скобках применим правило поглощения:
. Объединим первое и второе слагаемые, вынесем за скобки с, а к выражению в скобках применим правило поглощения: 
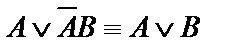
Получаем 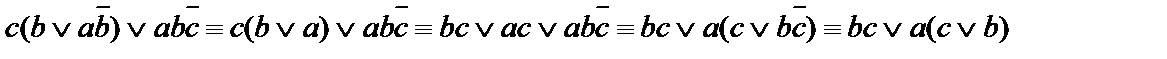 Найденному аналитическому выражению соответствует схема
Найденному аналитическому выражению соответствует схема
Задания для самостоятельной работы
Задание 1
Для заданной комбинационной схемы постройте аналитическое выражение, упростите его с помощью равносильных преобразований и, если возможно, нарисуйте упрощенную схему.
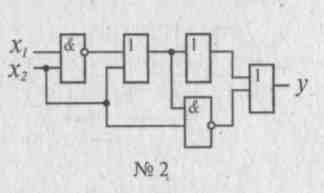 |
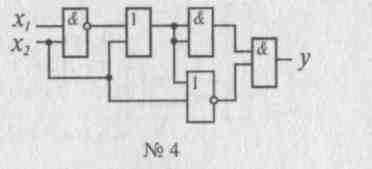 |
Задание 2
Для заданной логической таблицы функции y(a,b,c)) запишите аналитическое выражение и постройте комбинационную схему.
Вариант 1
| Вариант 2
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Вариант 3
| Вариант 4
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Вариант 5
| Вариант 6
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Вариант 7
| Вариант 8
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Вариант 9
| Вариант 10
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Вариант 11
| Вариант 12
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Вариант 13
| Вариант 14
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Вариант 15
| Вариант 16
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Вариант 17
| Вариант 18
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Вариант 19
| Вариант 20
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Вариант 21
| Вариант 22
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Вариант 23
| Вариант 24
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Вариант 25
|
