Апостериорная оценка точности рассчитанных координат

В априорной оценке использовалась информация о точности, полученная по результатам предыдущих измерений, а в апостериорной оценке участвуют текущие измерения, по которым была вычислена вероятнейшая точка.

Допустим, что ковариационная матрица погрешностей измерений D известна с точностью до постоянного множителя т²:

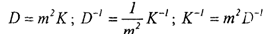
где матрица К— известна, а величина т² — неизвестна.

Иными словами, известны относительные, а не абсолютные значения матрицы D. С учетом этого рассмотрим систему нормальных уравнений

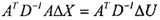
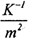, получим:

Подставив в уравнение вместо D~' выражение

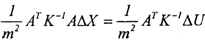
Величина т² (дисперсия наблюдения с единичным весом) сокращается и решение, в итоге, не зависит от абсолютной величины элементов ковариационной матрицы измерений D. Матрицу К~' также называют «весовой» и обозначают через W, а т² - дисперсией наблюдения с единичным весом. Если т не выносилась из D, то весовой будет просто D~'.

Рассмотрим величину, представляющую собой обобщенную (взвешенную) остаточную сумму квадратов уклонений:

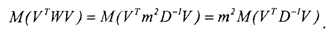
Здесь М — операция взятия математического ожидания, которую упрощенно можно рассматривать как отыскание среднего значения.

Рассмотрим выражение V^TD~^lУ пока без операции взятия математического ожидания:

V^'D-'V = V'D-^AU - ААХ) = V^-'^U - V⁷ D~'АЬХ

Последнее слагаемое равно нулю. Это видно из условия (2.17) и рис. 2.6, поскольку векторы V^r D'¹ и ААХ ортогональны, а скалярное произведение таких

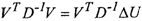векторов равно нулю. Тогда

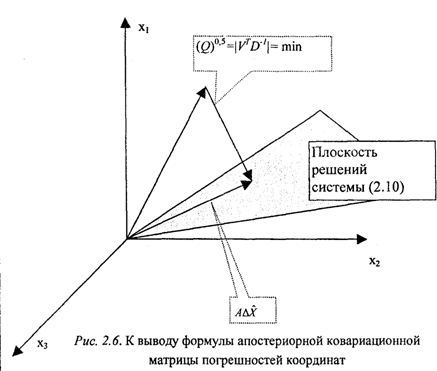
Кроме того,

Т 1 Т -Т Т -1 Т 1 'Т Т -1 V¹ D'^AU = (•AU¹ - AX¹ A¹ )D 'W = AC/⁷ D ^l &U - &X¹ A¹ D ' MJ .

т f Во втором слагаемом произведение A D~ Ш представляет собой правую часть

системы нормальных уравнений (2.19). Записав вместо нее левую часть этой

системы (A^TD~¹A}^X, окончательно получим формулу, по которой можно рассчитать значение квадратичного критерия (остаточную сумму квадратов невязок):

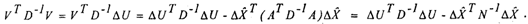
Здесь /\U - вектор, рассчитанный по исходным данным Uu - Uc, и первое слагаемое в правой части дают значение остаточной суммы в начальной (счислимой) точке, а второе — уменьшает это значение за счет смещения к оптимальной точке на величину д^ .

С учетом взятия операции математического ожидания (2.33) справедливо выражение:

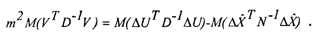
Распишем второе слагаемое:

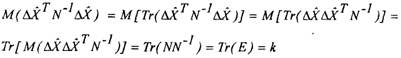
С учетом выражения (2.35) получим

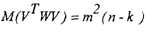
Несмещенная оценка т² запишется в виде выражения

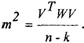
Тогда апостериорную оценку ковариационной матрицы погрешности резуль­татов получим следующим образом:

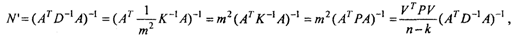
или апостериорная ковариационная матрица погрешностей координат рассчитыва­ется через априорную матрицу так:

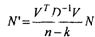
Пример. Определить координаты места судна и поправку компаса по измерениям четырех пеленгов. Рассчитать элементы априорного и апостериорного эллипсов погрешностей координат и средние квадратические погрешности обсервации.

Задачу решить на плоскости в прямоугольных координатах согласно значениям, представленным в табл. 2.2, используя два последовательных приближения.

Окончательный ответ дать в географической системе координат.

Счислимые координаты: х = 8,0 миль; у = 4,4 миль.

Таблица 2.2

Координаты ориентиров	Обсервованные пеленги ориентиров	СКП измерения пеленгов
^ai	Ул	П"	7»°
16,3	7,9	25,5	0,2
12,0	9,8	56,6	0,2
5,4	11,8	112,6	0,2
14,2	3,0	350,1	0,2

Решение Первая итерация

1. Запишем навигационную функцию пеленга (1.10) с учетом поправки Z:

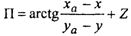
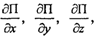из которых

2. Рассчитаем производные на счислимые координаты

составим матрицу А.

3. По навигационной функции рассчитаем счислимьге пеленги по счислимьм координатам и координатам навигационных ориентиров, полагая поправку Z=0 на первой итерации.

4. Вычислим вектор свободных членов Д?7, а также вектор &Хи вектор координат Ху, и ковариационную матрицу погрешностей координат N. Далее приведены вычисления:

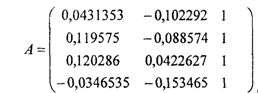
/ / Пд1 = +0,399061 , Пс2 = +0,933248,М1сз = +1,908675, П^ = +6,061103

Затем из априорной ковариационной матрицы N выбираем верхний левый блок ni, который определяет точность координат х,у и по формулам (2.26) - (2.29), находим элементы априорного эллипса погрешностей обсервации и СКП М.

Элементы априорного эллипса погрешностей обсервации из N':

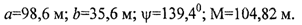
Элементы апостериорного эллипса погрешностей обсервации из верхнего левого блока матрицы (2.36):

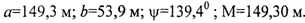
Вторая итерация:

\. Обсервованные координаты принимаем за счислимые, т.е. Хс = Ху, и

повторяем вычисления по формулам ( 2.20) и (2.26) - (2.29) с расчетом оценки точности координат.

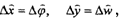определяем

2. Учитывая принятые обозначения, а именно

географические координаты при известных географических координатах счислимой точки С (©с, ^с)-'

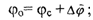
^о^с⁺ Aw cos (pm, где <pm ⁼ (фс + <ро)/2 - средняя широта

Графоаналитический расчет

1. На листе миллиметровой бумаги строим систему координат с началом в счислимой точке и выбираем масштаб для прокладки (рис. 2.7).

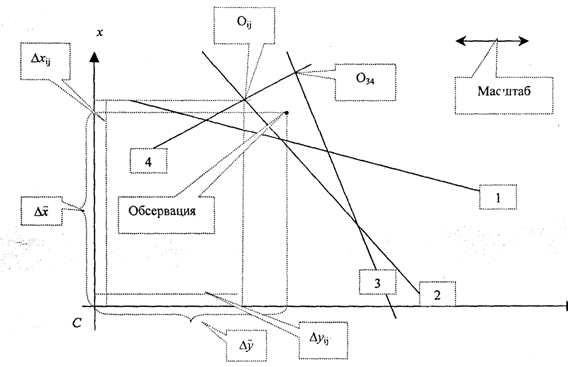
Рис. 2.7. Графоаналитический расчет координат места судна

2. Производим прокладку линий положения, используя формулу Дп, =—'-, и Si

получаем фигуру погрешностей координат.

3. Определяем приращения координат каждой из вершин фигуры погрешностей ау,/, Ауу.

4. Каждая точка пересечения двух линий положения Оу имеет вес, который можно рассчитать по следующей формуле:

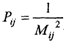
где My — средняя квадратическая погрешность точки по двум линиям положения. 5. Находим средневзвешенное значение приращений координат относительно счислимой точки:

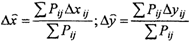
6. Находим обсервованные прямоугольные координаты, используя формулу (2.8), а также географические координаты по формулам, приведенным во второй итерации.

7. Для сравнения сгавим точку по первой итерации на диаграмму графоаналитического расчета.