Лекция 1. Числовые множества. Комплексные числа

Лекция 1. Числовые множества. Комплексные числа

I. Аксиоматическое построение множества действительных чисел

Множество натуральных и целых чисел.

Множество рациональных чисел.

Аксиоматическое построение множества действительных чисел.

4. Расширенная числовая прямая. Окрестности конечных точек и .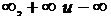

Комплексные числа.

Одним из основных объектов математики является число. Среди бесконечных числовых множеств выделяют:

N - множество натуральных чисел, предназначенных для счета предметов. Во множестве натуральных чисел выполнимы операции сложения, умножения, возведения в степень, тогда как операции вычитания, деления и извлечения корня некоторой степени не всегда выполнимы. Существует несколько теорий натуральных чисел, например, N - множество, содержащее самое маленькое число 1, и, за любым числом n всегда следует (n+1) и др.

Z - множество целых чисел (нуль, все натуральные и им противоположные – отрицательные числа). Во множестве целых чисел всегда могут быть совершены операции сложения, вычитания, умножения, возведения в степень, тогда как операции деления и извлечения корня некоторой степени не всегда выполнимы. На первый взгляд множество Z казалось бы, гораздо богаче числами, чем множество N, но это не так 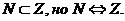Эквивалентность данных множеств устанавливается с помощью взаимно-однозначного соответствия: 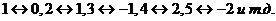(четным числам – положительные целые, нечетным – отрицательные).

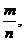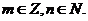Q – множество рациональных чисел, это множество дробей вида где Множество рациональных чисел обладает свойством счётности (есть несколько способов подсчета рациональных чисел – табличный, с помощью взаимно-однозначного соответствия с точками плоскости и др.). Рациональные числа удобно располагать на числовой прямой (оси).

Каждому рациональному числу соответствует точка на числовой оси, но не каждой точке на числовой оси соответствует рациональное число ( 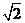), доказательство несоизмеримости диагонали квадрата с его стороной основано на применении теоремы Пифагора и свойствах делимости натуральных чисел:

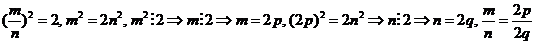, пришли к противоречию, что дробь 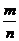несократима. Возникает необходимость расширения множества рациональных чисел, вновь водимые числа – иррациональные I, а их объединение образует множество действительных чисел R.

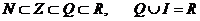
К возникновению множеств N,Z и Q привели практические потребности людей считать, указывать направление счета (долг-прибыль, верх-низ, право-лево и т.д.) и делить целое на части, а множества I, R и Cобразовались в связи с потребностями самой математики.

При обращении любой обыкновенной дроби в десятичную получается либо конечная, либо бесконечная периодическая десятичная дробь: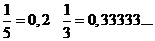

Любая периодическая десятичная дробь может быть обращена в обыкновенную по формуле суммы бесконечно убывающей геометрической прогрессии: 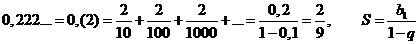, 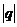<1.

Иррациональное число выражается бесконечной непериодической дробью.

Варианты индивидуальных заданий

Лекция 1. Числовые множества. Комплексные числа