Раздел 1. Основания математики
СОДЕРЖАНИЕ
1. Цели и задачи освоения дисциплины………………………………......... 4
2. Место дисциплины в структуре образовательной программы……….... 4
3. Результаты освоения дисциплины………………………………………...5
4. Структура и содержание дисциплины…………………………………… 7
4.1. Объем дисциплины и виды контактной и самостоятельной
работы ………………………………………...……………….………………7
4.2. Содержание и тематическое планирование дисциплины………...……8
4.3. Содержание разделов (тем) дисциплины …….……..………………….9
5.Образовательные технологии……..……………………………….……..11
6.Учебно-методические материалы………………………….……………..12
6.1. Задания и методические указания по организации и проведению практическихзанятий............……………………...………….…….......…………12
6.2. Задания и методические указания по организации самостоятельной работы студента………...………………………………….……………..………..14
6.3. Вопросы для подготовки к зачету..........................................................18
7. Учебно-методическое и информационное обеспечение……..….……..21
8.Материально-техническоеобеспечение дисциплины…….….……..…...22
ЦЕЛИ и задачи ОСВОЕНИЯ ДИСЦИПЛИНЫ
Цели преподавания дисциплины «Математика»:
– формирование личности студента, развитие интеллекта, способности к логическому и алгоритмическому мышлению;
– привитие знаний основных математических методов и математического аппарата, используемого при изучении общенаучных и специальных дисциплин;
– развитие математической культуры у обучающегося, навыков применения математических методов и основ математического моделирования при решении практических задач.
Задачами изучения курса математики являются:
– усвоение студентами основных математических понятий;
– приобретение твердых навыков решения основных математических задач, являющихся моделями прикладных задач;
– развитие на этой базе логического и алгоритмического мышления;
– овладение умением при решении задач выбирать и использовать оптимальные математические методы, анализировать полученные результаты;
– освоение навыков самостоятельного изучения литературы, содержащей математический аппарат; пользования справочной литературой.
МЕСТО ДИСЦИПЛИНЫ В СТРУКТУРЕ ОПОП ВО
Дисциплина «Математика» относится к общенаучному модулюосновных образовательных программ.
Для изучения данной учебной дисциплины необходимы знания, умения и навыки, формируемые при изучении курса математики средней школы.
Знания, полученные студентами при изучении курса "Математика ", будут использованы ими при освоении различных курсов. Среди них:
· Прикладная математика
· Статистика
· Теоретическая механикаи сопротивление материалов
· Физика
· Начертательная геометрия и компьютерная инженерная графика
· Электротехника и электропривод
· Экономика
· Методы математической обработки данных психолого-педагогических исследований
· Теория систем и системный анализ
· Методы измерения качества продукции
РЕЗУЛЬТАТы ОСВОЕНИЯ ДИСЦИПЛИНЫ
Дисциплина «Математика» способствует формированию следующих компетенций, предусмотренных ФГОС по направлению подготовки
Таблица 1
| ФГОС направления подготовки | компетенция | содержание компетенции |
| 09.03.02 | (ОПК-2) | способность использовать основные законы естественнонаучных дисциплин в профессиональной деятельности, применять методы математического анализа и моделирования, теоретического и экспериментального исследования |
| 09.03.03 | (ОПК-3) | способность использовать основные законы естественнонаучных дисциплин и современные информационно-коммуникационные технологии в профессиональной деятельности |
| 13.03.02 | (ОПК-2) | способность применять соответствующие физико-математический, аппарат методы анализа и моделирования теоретического и экспериментального исследования при решении профессиональных задач |
| 15.03.01 | (ОПК-1) | умение использовать основные законы естественнонаучных дисциплин в профессиональной деятельности, применять методы математического анализа и моделирования, теоретического и экспериментального исследования |
| 38.03.01 | (ОПК-2) | способность осуществлять сбор, анализ и обработку данных необходимых для решения профессиональных задач |
| 39.03.01 | (ОПК-6) | способность использовать основные законы естественнонаучных дисциплин в профессиональной деятельности, применять методы математического анализа и моделирования, теоретического и экспериментального исследования |
| 44.03.02 | ОПК-2 | готовность применять качественные и количественные методы в психологических и педагогических исследованиях |
| 44.03.04 | (ОК-3) | способность использовать основы естественнонаучных и экономических знаний при оценке эффективности результатов деятельности в различных сферах |
| (ОПК-2) | способность выявлять естественнонаучную сущность проблем, возникающих в ходе профессионально-педагогической деятельности | |
| 46.03.02 | (ОК-10) | способностью к использованию основных методов, способов и средств получения, хранения, переработки информации |
По окончании изучения курса студент должен:
Знать:
· Основы теории множеств и математической логики.
· Основы линейной алгебры и аналитической геометрии.
· Дифференциальное исчисление функций одной независимой переменной. Основы математического анализа функции нескольких независимых переменных.
Уметь:
· Свободно оперировать математическими понятиями и категориями, доказывать несложные математические утверждения.
· Строить алгоритмы решения задач, связанных с основными математическими моделями.
· Использовать базовые знания математических дисциплин в профессиональной деятельности.
· Проводить анализ решений задач, самостоятельно разбираться в математическом аппарате, содержащемся в литературе, связанной со специальностью студента.
Владеть / быть в состоянии продемонстрировать:
· Твердые навыки решения основных задач математики.
· Логическое и алгоритмическое мышление.
· Основы математического моделирования.
· Владение методами математического анализа.
4. СТРУКТУРА и содержание ДИСЦИПЛИНЫ
4.1.Объем дисциплины и виды контактной и самостоятельной работы
Общая трудоёмкость дисциплины составляет 3 зачетных единиц (108 часов), их распределение по видам работ представлено в табл. 2.
Таблица 2
Распределение трудоемкости дисциплины по видам работ
| Объемы учебной работы, перечень и сроки контрольных мероприятий | Формы обучения | ||
| Очная | Заочная | ||
| Виды и объемы учебной работы, в ч | |||
| Общая трудоемкость дисциплины в часах (в зачетных ед.) | (3) | (3) | |
| Контактная работа, в том числе: | |||
| Лекции | |||
| Практические занятия | |||
| Лабораторные работы | - | - | |
| Самостоятельная работа студента (СРС) (всего) | |||
| В том числе: | |||
| Расчетно-графические работы (РГР, КР) | |||
| Самоподготовка к текущему контролю знаний | |||
| Другие виды СРС | |||
| Подготовка к зачету |
4.2. Содержание и тематическое планирование дисциплины
Тематический план дисциплины
Таблица 3
| Раздел дисциплины | Семестр | Всего, час. | Вид контактной работы, час. | Формы текущего контроля успеваемости (по неделям семестра) Форма промежуточной аттестации (по семестрам) | |||||
| Лекции | Практ. занятия | Лаб. работы | Др. формы контактной работы | Из них, в интерактивной форме | Самотастотельнамя работа | ||||
| Раздел 1. Основания математики | Домашние задания | ||||||||
| Тема 1.1. Элементы математической логики | Домашние задания | ||||||||
| Тема 1.2. Элементы теории множеств | Домашние задания | ||||||||
| Тема 1.3. Элементы теории графов | Домашние задания | ||||||||
| Раздел 2.Элементы линейной алгебры и аналитической геометрии | Домашние задания. Расчетно-графическая работа №1. | ||||||||
| Тема 2.1. Алгебра матриц, Линейные системы уравнений | Тест «Вычисление определителей» | ||||||||
| Тема2.2. Векторная алгебра | Тест «Операции над векторами» | ||||||||
| Тема 2.3. Аналитическая геометрия | Домашние задания | ||||||||
| Раздел 3.Элементыматематическогоанализа | Домашние задания. | ||||||||
| Тема 3.1. Предел и непрерывность функции | Тест «Вычисление пределов» Домашние задания | ||||||||
| Тема 3.2. Производная функции и ее свойства | Тест «Вычисление производной» | ||||||||
| Тема 3.3. Приложения производной | Домашние задания | ||||||||
| Всего по дисциплине | Зачет с оценкой |
Практические занятия
Таблица 4
| № раздела | Наименование практических работ | Кол-во ауд.часов |
| Элементы математической логики | ||
| Элементы теории множеств | ||
| Элементы теории графов | ||
| Алгебра матриц, Линейные системы уравнений | ||
| Векторная алгебра | ||
| Аналитическая геометрия | ||
| Предел и непрерывность функции | ||
| Производная функции и ее свойства | ||
| Приложения производной |
4.3. Содержание разделов (тем) дисциплины
Тема 2.2.Векторная алгебра
Векторы в трехмерном пространстве, линейные операции над ними. Линейно зависимые и линейно независимые системы векторов. Базис и координаты вектора. Скалярное произведение векторов, его свойства, выражение в координатах. Векторное исмешанноепроизведениявекторов.Их свойства и вычисление.
Задания и методические указания по организации и проведению практических занятий
Расчетно-графические работы
Вариантырасчетно-графической работы
Вариант №1
1. Вычислить определитель: 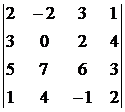 .
.
2. Найти АВ–ВА, где: 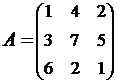 ;
; 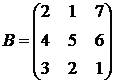 .
.
3. Найти А-1, где: 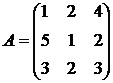 , сделать проверку, и решить систему АХ=
, сделать проверку, и решить систему АХ= 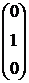 матричным способом.
матричным способом.
4. Решить систему а) методом Крамера; б) методом Гаусса:
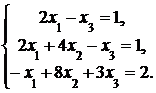 Сделать проверку.
Сделать проверку.
5. Три стороны треугольника АВС заданы уравнениями:
(АВ): х-3у-23=0; (ВС): 7х+9у+19=0; (АС): 4х+3у+13=0. Составить уравнение высоты, проведенной из вершины В и уравнение медианы, проведенной из вершины А.
6. Даны координаты вершин пирамиды 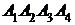 .
.
Найти: 1) длину ребра 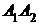 ; 2) угол между ребрами
; 2) угол между ребрами 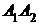 и
и 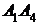 ; 3) угол между ребром
; 3) угол между ребром 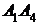 и гранью
и гранью 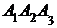 ; 4) площадь грани
; 4) площадь грани 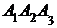 ; 5) объем пирамиды. Сделать чертеж.
; 5) объем пирамиды. Сделать чертеж.
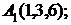
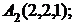
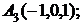
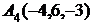 .
.
7. Найти точкуВ, симметричную точке А(1, 3, –4) относительно плоскости 3х+у–2z=0.
Вариант №2
1. Вычислить определитель: 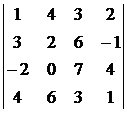 .
.
2. Найти АВ–ВА, где: 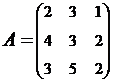 ;
; 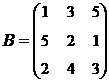 .
.
3. Найти А-1, где: 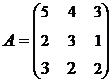 , сделать проверку, и решить систему АХ=
, сделать проверку, и решить систему АХ= 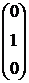 матричным способом.
матричным способом.
4. Решить систему а) методом Крамера; б) методом Гаусса:
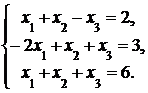 Сделать проверку.
Сделать проверку.
5. Даны уравнения одной из сторон ромба 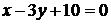 и одной из его диагоналей
и одной из его диагоналей 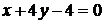 ; диагонали ромба пересекаются в точке
; диагонали ромба пересекаются в точке 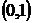 .
.
Найти уравнения остальных сторон ромба.
6. Даны координаты вершин пирамиды 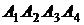 .
.
Найти: 1) длину ребра 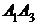 ; 2) угол между ребрами
; 2) угол между ребрами 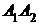 и
и 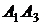 ; 3) угол между ребром
; 3) угол между ребром 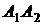 и гранью
и гранью 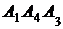 ; 4) площадь грани
; 4) площадь грани 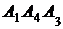 ; 5) объем пирамиды. Сделать чертеж.
; 5) объем пирамиды. Сделать чертеж.
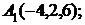
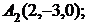
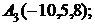
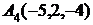 .
.
7. Найти точку М, симметричную точке N(1, 3, 5) относительно плоскости 2х–у–3z+5=0.
Вариант №3
1. Вычислить определитель: 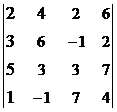 .
.
2. Найти АВ–ВА, где: 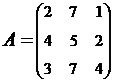 ;
; 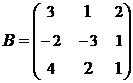 .
.
3. Найти А-1, где: 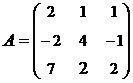 , сделать проверку, и решить систему АХ=
, сделать проверку, и решить систему АХ= 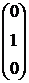 матричным способом.
матричным способом.
4. Решить систему а) методом Крамера; б) методом Гаусса:
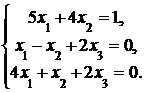 Сделать проверку.
Сделать проверку.
5. Даны две вершины 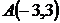 и
и 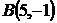 и точка
и точка 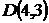 пересечения высот треугольника. Составить уравнения его сторон.
пересечения высот треугольника. Составить уравнения его сторон.
6. Даны координаты вершин пирамиды 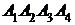 .
.
Найти: 1) длину ребра 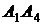 ; 2) угол между ребрами
; 2) угол между ребрами 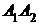 и
и 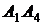 ; 3) угол между ребром
; 3) угол между ребром 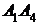 и гранью
и гранью 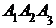 ; 4) площадь грани
; 4) площадь грани 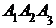 ; 5) объем пирамиды. Сделать чертеж.
; 5) объем пирамиды. Сделать чертеж.
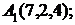
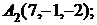
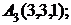
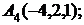
7. Найти проекцию точки Р(2, –5,7) на прямую, проходящую через точки М1(4, 5, 6) и М2(–2, –17, –8).
Вариант №4
1. Вычислить определитель: 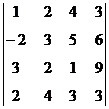 .
.
2. Найти АВ–ВА, где: 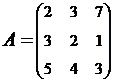 ;
; 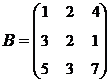 .
.
3. Найти А-1, где: 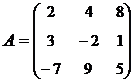 , сделать проверку, и решить систему АХ=
, сделать проверку, и решить систему АХ= 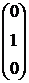 матричным способом.
матричным способом.
4. Решить систему а) методом Крамера; б) методом Гаусса:
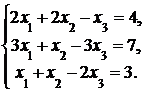 Сделать проверку.
Сделать проверку.
5. Уравнения двух сторон параллелограмма 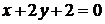 и
и 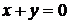 , а уравнение одной из его диагоналей
, а уравнение одной из его диагоналей 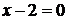 .Найти координаты вершин параллелограмма.
.Найти координаты вершин параллелограмма.
6. Даны координаты вершин пирамиды 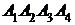 .
.
Найти: 1) длину ребра 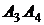 ; 2) угол между ребрами
; 2) угол между ребрами 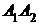 и
и 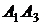 ; 3) угол между ребром
; 3) угол между ребром 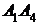 и гранью
и гранью 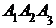 ; 4) площадь грани
; 4) площадь грани 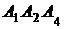 ; 5) объем пирамиды. Сделать чертеж.
; 5) объем пирамиды. Сделать чертеж.
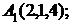
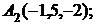
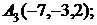
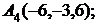
7. Найти точку Q, симметричную точке Р(4, 1, 6) относительно прямой
Вариант №5
1. Вычислить определитель: 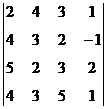 .
.
2. Найти АВ–ВА, где: 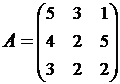 ;
; 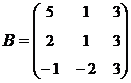 .
.
3. Найти А-1, где: 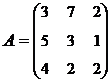 , сделать проверку, и решить систему АХ=
, сделать проверку, и решить систему АХ= 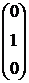 матричным способом.
матричным способом.
4. Решить систему а) методом Крамера; б) методом Гаусса:
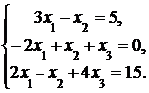 Сделать проверку.
Сделать проверку.
5. Три стороны треугольника 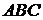 заданы уравнениями
заданы уравнениями 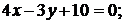
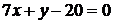 и
и 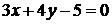 . Написать уравнение высоты и биссектрисы, проведенных из вершины
. Написать уравнение высоты и биссектрисы, проведенных из вершины 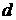 .
.
6. Даны координаты вершин пирамиды 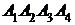 .
.
Найти: 1) длину ребра 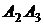 ; 2) угол между ребрами
; 2) угол между ребрами 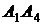 и
и 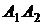 ; 3) угол между ребром
; 3) угол между ребром 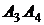 и гранью
и гранью 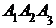 ; 4) площадь грани
; 4) площадь грани 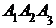 ; 5) объем пирамиды. Сделать чертеж.
; 5) объем пирамиды. Сделать чертеж.
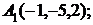
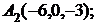
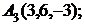
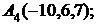
6. Найти точку Q, симметричную точке Р(2, –5, 7) относительно прямой 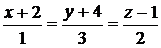
Вариант №6
1. Вычислить определитель: 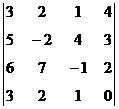 .
.
2. Найти АВ–ВА, где: 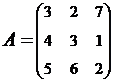 ;
; 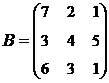 .
.
3. Найти А-1, где: 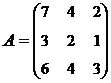 , сделать проверку, и решить систему АХ=
, сделать проверку, и решить систему АХ= 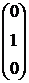 матричным способом.
матричным способом.
4. Решить систему а) методом Крамера; б) методом Гаусса:
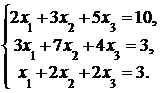 Сделать проверку.
Сделать проверку.
5. Даны вершины 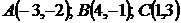 трапеции
трапеции 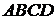
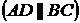 . Известно, что диагонали трапеции взаимно перпендикулярны. Найти координаты вершины
. Известно, что диагонали трапеции взаимно перпендикулярны. Найти координаты вершины 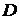 этой трапеции.
этой трапеции.
6. Даны координаты вершин пирамиды 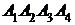 .
.
Найти: 1) длину ребра 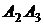 ; 2) угол между ребрами
; 2) угол между ребрами 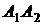 и
и 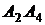 ; 3) угол между ребром
; 3) угол между ребром 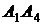 и гранью
и гранью 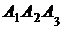 ; 4) площадь грани
; 4) площадь грани 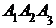 ; 5) объем пирамиды. Сделать чертеж.
; 5) объем пирамиды. Сделать чертеж.
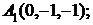
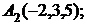
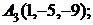
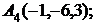
7. Найти проекцию точки А(2, 0, 3) на прямую 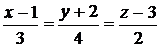 .
.
Вариант №7
1. Вычислить определитель: 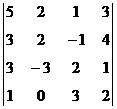 .
.
2. Найти АВ–ВА, где: 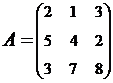 ;
; 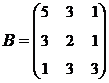 .
.
3. Найти А-1, где: 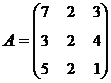 , сделать проверку, и решить систему АХ=
, сделать проверку, и решить систему АХ= 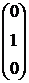 матричным способом.
матричным способом.
4. Решить систему а) методом Крамера; б) методом Гаусса:
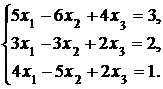 Сделать проверку.
Сделать проверку.
5. Даны уравнения двух сторон треугольника 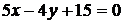 и
и 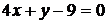 . Его медианы пересекаются в точке
. Его медианы пересекаются в точке 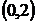 .Составить уравнение третьей стороны треугольника.
.Составить уравнение третьей стороны треугольника.
6. Даны координаты вершин пирамиды 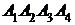 .
.
Найти: 1) длину ребра 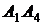 ; 2) угол между ребрами
; 2) угол между ребрами 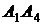 и
и 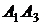 ; 3) угол между ребром
; 3) угол между ребром 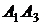 и гранью
и гранью 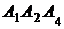 ; 4) площадь грани
; 4) площадь грани 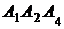 ; 5) объем пирамиды. Сделать чертеж.
; 5) объем пирамиды. Сделать чертеж.
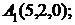
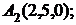
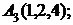
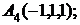
7. Найти проекцию точки А(1, –1, 2) на плоскость х+у+2z–3=0.
Вариант №8
1. Вычислить определитель: 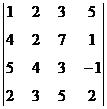 .
.
2. Найти АВ–ВА, где: 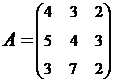 ;
; 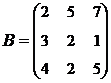 .
.
3. Найти А-1, где: 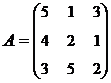 , сделать проверку, и решить систему АХ=
, сделать проверку, и решить систему АХ= 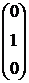 матричным способом.
матричным способом.
4. Решить систему а) методом Крамера; б) методом Гаусса:
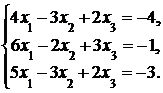 Сделать проверку.
Сделать проверку.
5. Даны две вершины 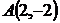 и
и 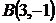 и точка
и точка  пересечения медиан треугольника
пересечения медиан треугольника 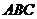 . Составить уравнение высоты треугольника, проведенной через третью вершину С.
. Составить уравнение высоты треугольника, проведенной через третью вершину С.
6. Даны координаты вершин пирамиды 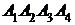 .
.
Найти: 1) длину ребра 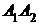 ; 2) угол между ребрами
; 2) угол между ребрами 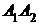 и
и 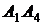 ; 3) угол между ребром
; 3) угол между ребром 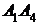 и гранью
и гранью 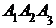 ; 4) площадь грани
; 4) площадь грани 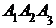 ; 5) объем пирамиды. Сделать чертеж.
; 5) объем пирамиды. Сделать чертеж.
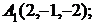
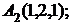
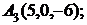
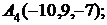
7. Найти проекцию точки М(0, –3, –2) на прямую 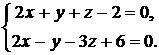
Вариант №9
1. Вычислить определитель: 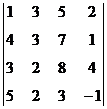 .
.
2. Найти АВ–ВА, где: 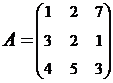 ;
; 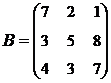 .
.
3. Найти А-1, где: 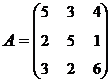 , сделать проверку, и решить систему АХ=
, сделать проверку, и решить систему АХ= 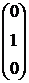 матричным способом.
матричным способом.
4. Решить систему а) методом Крамера; б) методом Гаусса:
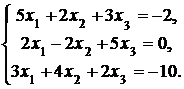 Сделать проверку.
Сделать проверку.
5. Уравнения двух высот треугольника 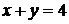 и
и 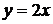 , и одна из его вершин А(0;2). Составить уравнение сторон треугольника.
, и одна из его вершин А(0;2). Составить уравнение сторон треугольника.
6. Даны координаты вершин пирамиды 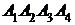 .
.
Найти: 1) длину ребра 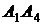 ; 2) угол между ребрами
; 2) угол между ребрами 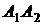 и
и 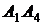 ; 3) угол между ребром
; 3) угол между ребром 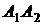 и гранью
и гранью 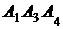 ; 4) площадь грани
; 4) площадь грани 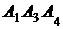 ; 5) объем пирамиды. Сделать чертеж.
; 5) объем пирамиды. Сделать чертеж.
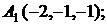
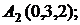
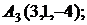
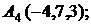
7. Найти проекцию точки М(3, 3, 3) на прямую 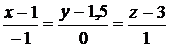 .
.
Вариант №10
1. Вычислить определитель: 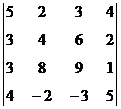 .
.
2. Найти АВ–ВА, где: 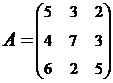 ;
; 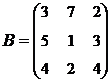 .
.
3. Найти А-1, где: 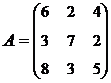 , сделать проверку, и решить систему АХ=
, сделать проверку, и решить систему АХ= 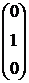 матричным способом.
матричным способом.
4. Решить систему а) методом Крамера; б) методом Гаусса:
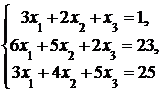 Сделать проверку.
Сделать проверку.
5. Даны уравнения двух медиан треугольника 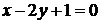 и
и 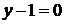 и одна из его вершин (1;3). Составить уравнения его сторон.
и одна из его вершин (1;3). Составить уравнения его сторон.
6. Даны координаты вершин пирамиды 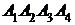 .
.
Найти: 1) длину ребра 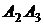 ; 2) угол между ребрами
; 2) угол между ребрами 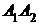 и
и 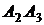 ; 3) угол между ребром
; 3) угол между ребром 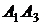 и гранью
и гранью 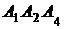 ; 4) площадь грани
; 4) площадь грани 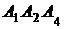 ; 5) объем пирамиды. Сделать чертеж.
; 5) объем пирамиды. Сделать чертеж.
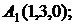
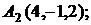
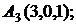
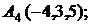
7. Найти точку К, симметричную точке М(1, 0, –1) относительно плоскости 2у+4z–1=0.
Варианты контрольной работы для студентов заочной формы обучения
Задача 1.
1.1. Граф, имеет матрицу инциденций  . Построить граф. Найти для него матрицу смежности.
. Построить граф. Найти для него матрицу смежности.
1.2. Граф, имеет матрицу смежности  . Построить граф. Найти для него матрицу инциденций..
. Построить граф. Найти для него матрицу инциденций..
1.3. Граф, имеет матрицу инциденций  . Построить граф. Найти для него матрицу смежности.
. Построить граф. Найти для него матрицу смежности.
1.4. Граф, имеет матрицу смежности  . Построить граф. Найти для него матрицу инциденций.
. Построить граф. Найти для него матрицу инциденций.
1.5. Граф, имеет матрицу инциденций  . Построить граф. Найти для него матрицу смежности.
. Построить граф. Найти для него матрицу смежности.
1.6. Граф, имеет матрицу смежности  . Построить граф. Найти для него матрицу инциденций.
. Построить граф. Найти для него матрицу инциденций.
1.7. Граф, имеет матрицу инциденций  . Построить граф. Найти для него матрицу смежности.
. Построить граф. Найти для него матрицу смежности.
1.8. Граф, имеет матрицу смежности  . Построить граф. Найти для него матрицу инциденций.
. Построить граф. Найти для него матрицу инциденций.
1.9. Граф, имеет матрицу инциденций  . Построить граф. Найти для него матрицу смежности.
. Построить граф. Найти для него матрицу смежности.
1.10. Граф, имеет матрицу смежности  . Построить граф. Найти для него матрицу инциденций.
. Построить граф. Найти для него матрицу инциденций.
Задача 2.
В пирамиде SABC: треугольник АВС – основание пирамиды, точка S – ее вершина. Даны координаты точек A, B, C, S.
2.1. А(-2;0;0); В(0;3;0); C(0;0;1); S(0;2;3).
2.2. А(4;0;0); В(0;-8;0); C(0;0;2); S(4;6;3).
2.3. А(-2;0;0); В(0;6;0); C(0;0;2); S(-1;6;4).
2.4. А(1;0;0); В(0;2;0); C(0;0;2); S(1;1;4).
2.5. А(-3;0;0); В(0;-2;0); C(0;0;1); S(-2;-1;3).
2.6. А(6;0;0); В(0;-3;0); C(0;0;2); S(4;-3;4).
2.7. А(3;0;0); В(0;-6;0); C(0;0;1); S(1;-3;3).
2.8. А(-4;0;0); В(0;4;0); C(0;0;2); S(-2;4;3).
2.9. А(-6;0;0); В(0;2;0); C(0;0;3); S(-3;2;5).
2.10. А(-1;0;0); В(0;5;0); C(0;0;2); S(-1;3;4).
Сделать чертеж. Найти:
1) длину ребра АВ;
2) угол между ребрами АВ и AS;
3) угол наклона ребра AS к основанию пирамиды;
4) площадь основания пирамиды;
5) объем пирамиды;
6) уравнение прямой АВ;
7) уравнение плоскости АВС;
8) проекцию вершины S на плоскость АВС;
9) длинувысоты пирамиды.
Задача 3.
Дана система линейных уравнений: 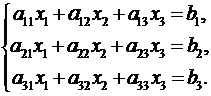
Доказать ее совместность и решить тремя способами: 1) методом Гаусса; 2) средствами матричного исчисления; 3) по правилу Крамера.
3.1. 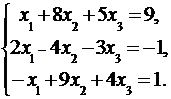 3.2.
3.2. 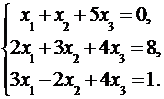
3.3. 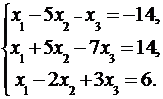 3.4.
3.4. 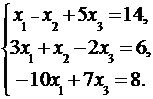
3.5. 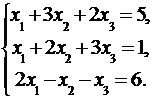 3.6.
3.6. 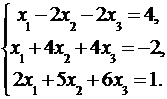
3.7. 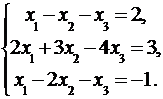 3.8.
3.8. 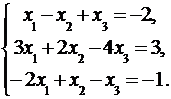
3.9. 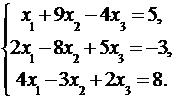 3.10.
3.10. 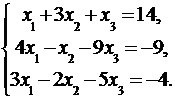
Задача 4.
Найти пределы функций, не пользуясь правилом Лопиталя.
4.1. а) 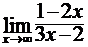 ; б)
; б) 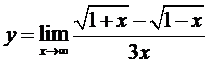 ;
;
в) 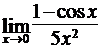 ; г)
; г) 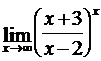 .
.
4.2. а) 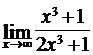 ; б)
; б) 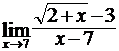 ;
;
в) 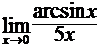 ; г)
; г) 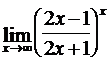 .
.
4.3. а) 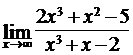 ; б)
; б) 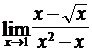 ;
;
в) 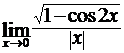 ; г)
; г) 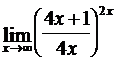 .
.
4.4. а) 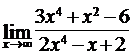 ; б)
; б) 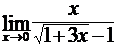 ;
;
в) 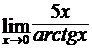 ; г)
; г) 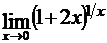 .
.
4.5. а) 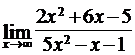 ; б)
; б) 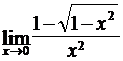 ;
;
в) 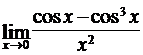 ; г)
; г) 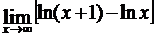 .
.
4.6. а) 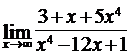 ; б)
; б) 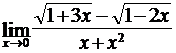 ;
;
в) 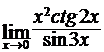 ; г)
; г) 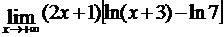 .
.
4.7. а) 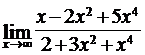 ; б)
; б) 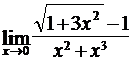 ;
;
в) 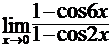 ; г)
; г)  .
.
4.8. а) 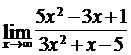 ; б)
; б) 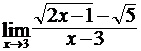 ;
;
в) 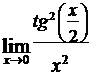 ; г)
; г) 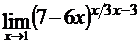 .
.
4.9. а) 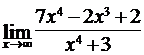 ; б)
; б) 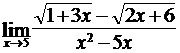 ;
;
в) 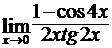 ; г)
; г) 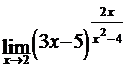 .
.
4.10. а) 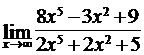 ; б)
; б) 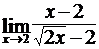 ;
;
в) 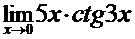 ; г)
; г) 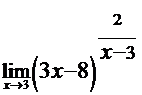 .
.
Задача 5.
Найти производные 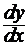 данных функций
данных функций
5.1. а) 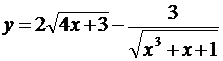 ; б)
; б) 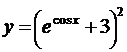 ;
;
в) 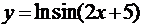 ; г)
; г) 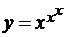 .
.
5.2. а) 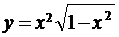 ; б)
; б) 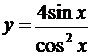 ; в)
; в) 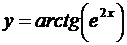 ;
;
г) 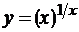 .
.
5.3. а) 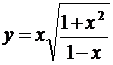 ; б)
; б) 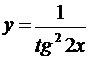 ; в)
; в) 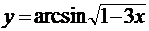 ;
;
г) 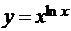 .
.
5.4. а) 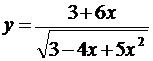 ; б)
; б) 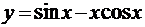 ;
;
в) 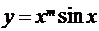 ; г)
; г) 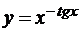 .
.
5.5. а) 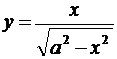 ; б)
; б) 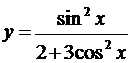 ; в)
; в) 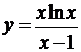 ;
;
г) 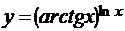 .
.
5.6. а) 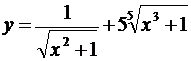 ; б)
; б) 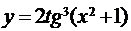 ;
;
в) 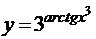 ; г)
; г) 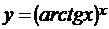 .
.
5.7. а) 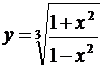 ; б)
; б) 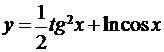 ;
;
в) 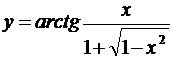 ; г)
; г) 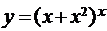 .
.
5.8. а) 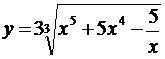 ; б)
; б) 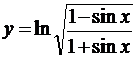 ;
;
в) 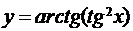 ; г)
; г) 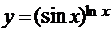 .
.
5.9. а) 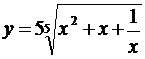 ; б)
; б) 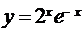 ; в)
; в) 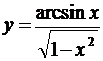 ;
;
г) 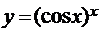 .
.
5.10. а) 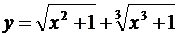 ; б)
; б) 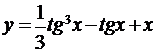 ;
;
в) 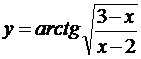 ; г)
; г) 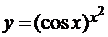 .
.
Задача 6.
а) Найти 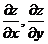 , если
, если
6.а.1 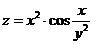 ; 6.а.2
; 6.а.2 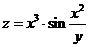 ; 6.а.2
; 6.а.2 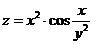
6.а.1 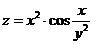 ; 6.а.2
; 6.а.2
