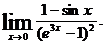Задача 1 . Вычислить пределы функций.
1. 
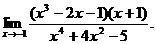
2. 
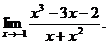
3. 
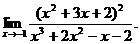
4. 
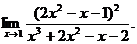
5. 
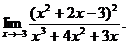
6.
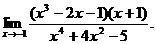
7. 
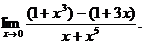
8. 
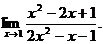
9. 
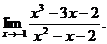
10. 
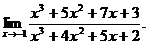
11. 
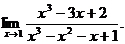
12. 
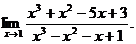
13. 
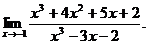
14. 
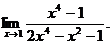
15. 
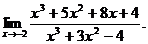
16. 
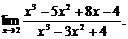
17. 
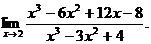
18. 
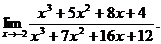
19. 
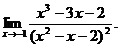
20. 
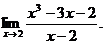
21. 
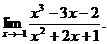
22. 
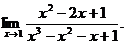
23.
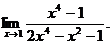
24. 
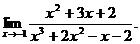
25. 
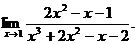
26. 
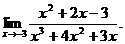
27. 
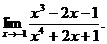
28. 
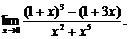
29. 
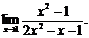
30. 
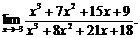
Задача 2. Вычислить пределы числовых последовательностей.
1. 
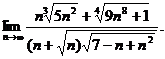
2. 
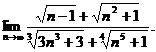
3. 
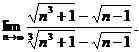
4. 
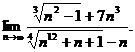
5. 
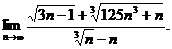
6. 
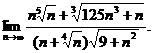
7. 
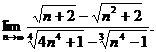
8. 
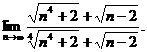
9. 
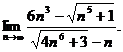
10. 
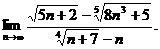
11. 
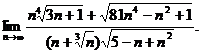
12. 
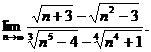
13. 
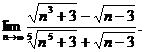
14. 
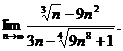
15. 
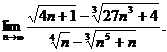
16. 
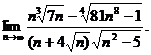
17. 
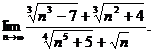
18. 
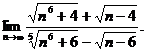
19. 
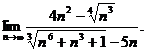
20. 
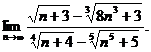
21. 
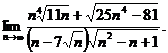
22. 
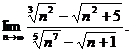
23. 
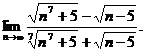
24. 
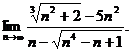
25. 
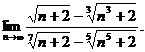
26. 
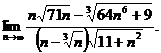
27. 
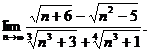
28. 
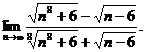
29. 
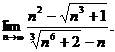
30. 
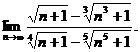
Задача 3 . Доказать (найти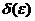 
), что:
1. 
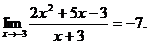
2. 
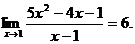
3. 
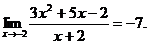
4. 
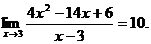
5. 
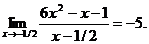
6. 
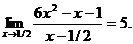
7. 
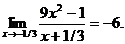
8. 
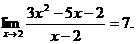
9. 
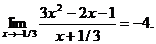
10. 
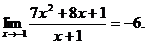
11. 
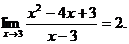
12. 
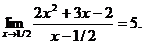
13. 
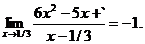
14. 
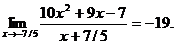
15. 
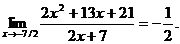
16. 
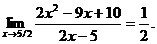
17. 
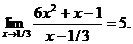
18. 
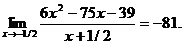
19. 
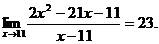
20. 
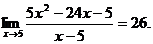
21. 
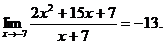
22. 
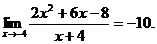
23. 
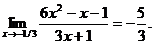
24. 
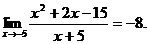
25. 
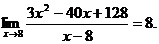
26. 
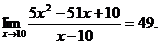
27. 
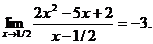
28. 
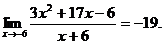
29. 
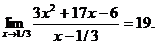
30. 
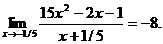
31. 
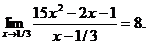
Задача 4. Вычислить пределы функций.
1. 
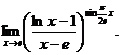
2. 
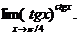
3. 
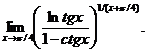
4. 
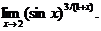
5. 
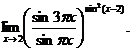
6. 
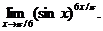
7. 
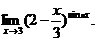
8. 
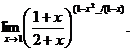
9. 
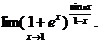
10. 
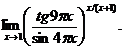
11. 
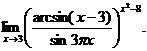
12. 
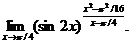
13. 
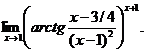
14. 
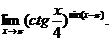
15. 
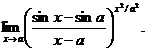
16. 
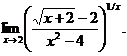
17. 
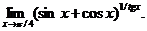
18. 
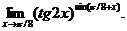
19. 
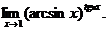
20. 
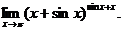
21. 
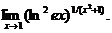
22. 
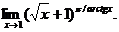
23. 
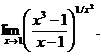
24. 
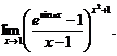
25. 
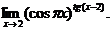
26. 
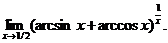
27. 
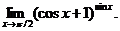
28. 
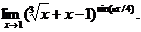
29. 
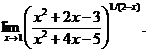
30. 
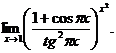
31. 
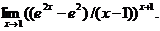
Задача 5. Вычислить предел функции или числовой последовательности.
1. 
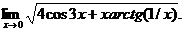
2. 
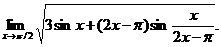
3. 
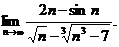
4. 
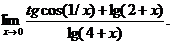
5. 
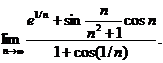
6. 
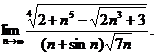
7. 
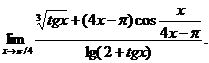
8. 
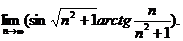
9. 
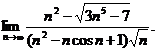
10. 
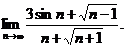
11. 
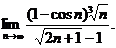
12. 
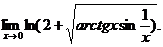
13. 
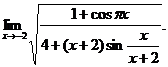
14. 
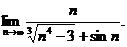
15. 
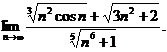
16. 
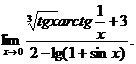
17. 
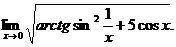
18. 
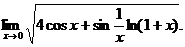
19. 
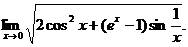
20. 
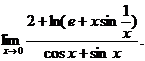
21. 
22. 
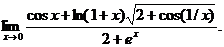
23. 
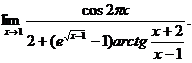
24. 
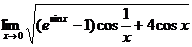
25. 
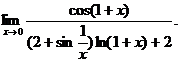
26. 
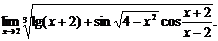
27. 
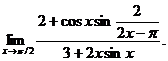
28. 
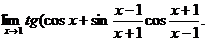
29. 
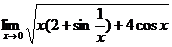
30. 
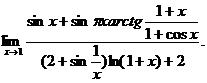
III. Непрерывность функции
Приращения аргумента и функции
Пусть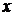 
есть некоторое значение данной переменной величины. Наряду с 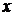рассмотрим другое значение 
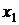этой переменной величины.
Определение. Приращением переменной величины называется разность между новым значением этой величины и ее прежним значением, т.е. приращение переменной величины равно
.
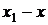Для обозначения приращения используется греческая буква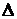 
.
Например,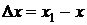 
обозначает приращение величины .
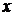Предположим, что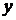 
есть некоторая функция от аргумента 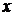, т.е.
.
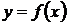Дадим аргументу 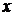приращение 
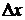; тогда 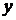получит соответствующее приращение 
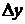. Этот факт можно записать так:
.
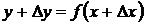Из двух последних равенств следует
.
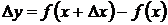Определение. Функция называется непрерывной в данной точке, если в этой точке бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.
Определение. Функция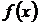 
называется непрерывной на данном множестве 
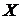, если:
1) она определена на этом множестве;
2) непрерывна в каждой точке этого множества.
Определение. Точка, в которой нарушается непрерывность функции, называется точкой разрыва этой функции.
Односторонние пределы
Скачок функции
Определение. Если значение функции 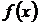стремится к числу 
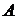, при 
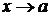со стороны меньших значений, то 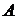называют левосторонним пределом функции 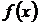и пишут:
.
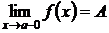Определение. Если значение функции 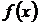стремится к числу 
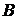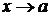, при со стороны больших значений, то 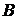называют правосторонним пределом функции 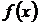и пишут:
.
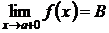Для чисел 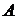и 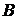употребляется символическая запись
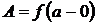и 
.
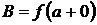Определение. Величина
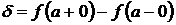
называется скачком функции 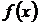в точке 
.
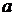Определение. Точка 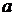разрыва функции 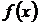называется точкой разрыва первого рада, если существуют конечные односторонние пределы функции
, 
.
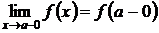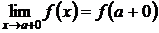Все прочие точки разрыва 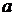функции 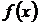называются ее точками разрыва второго рода.
Раскрытие неопределенностей
Может случиться, что функция 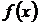определена и непрерывна всюду, за исключением некоторого значения 
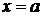, при котором функция 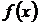теряет смысл (становится неопределенной).
Определение. Операция нахождения предела функци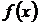и при 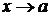в этом случае называется раскрытием неопределенности, а сам предел 
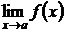, если он существует, называется истинным значением функци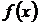и при .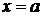
Решение типовых заданий
1.Вычислить предел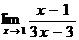 
.
,
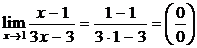отсюда следует, что функция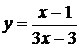 
не определена, а значит разрывна в точке 
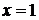. Выполним некоторые преобразования этой функции, а именно вынесем общий множитель знаменателя дроби за скобку. Получим:
.
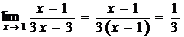2.Вычислить предел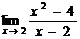 
.
.
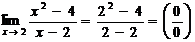Преобразуем функцию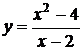 
, а именно применим формулу сокращенного умножения.
.
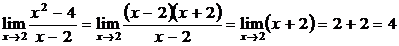3.Вычислить предел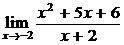 
.
,
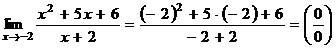Преобразуем функцию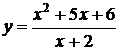 
, а именно разложим на множители квадратный трехчлен, находящийся в числителе, используя теорему Виета.
.
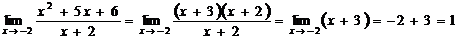4.Вычислить предел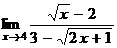 
.
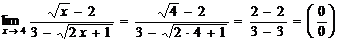
Преобразуем функцию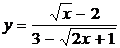 
, а именно используем умножение числителя и знаменателя на число сопряженное.
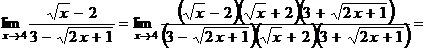
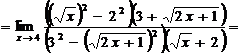
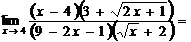
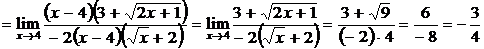
5.Вычислить предел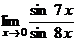 
.
Преобразуем функцию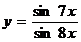 
, используя «замечательный предел»
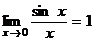. Получим
,
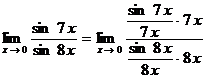так как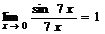 
и 
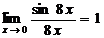, то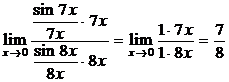 
.
6.Вычислить предел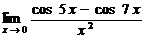 
.
Так как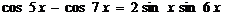 
, то
.
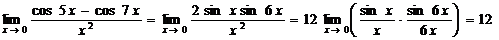Упражнения и задания для самостоятельной работы
Теоретические вопросы
1. Какая функция называется непрерывной в точке?
2. Дайте определение непрерывность сложной функции.
3. Сформулируйте свойства функций, непрерывных в точке.
4. Сформулируйте теорему о непрерывности обратной функций.
5. Что такое скачек функции?
Задание 1. Доказать, что функция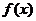 
непрерывна в точке 
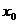(найти ).
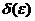1. 
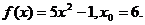
2. 
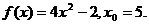
3. 
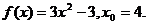
4. 
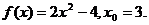
5. 
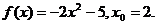
6. 
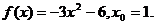
7. 
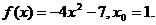
8. 
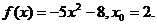
9. 
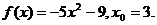
10. 
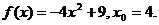
11. 
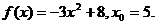
12. 
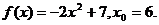
13. 
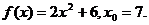
14. 
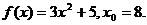
15. 
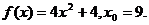
16. 
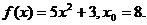
17. 
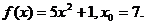
18. 
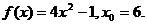
19. 
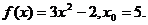
20. 
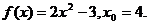
21. 
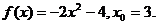
22. 
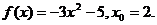
23. 
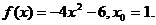
24. 
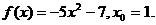
25. 
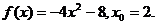
26. 
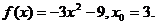
27. 
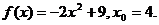
28. 
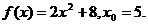
29. 
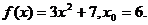
30. 
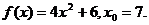
31. 
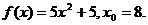
Задание 2. Пользуясь определением непрерывности "на языке
приращения", доказать непрерывность следующих функций в области
их определения.
1. 
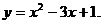
2. 
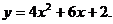
3. 
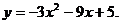
4. 
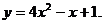
5. 
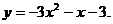
6. 
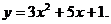
7. 
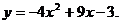
8. 
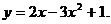
9. 
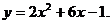
10. 
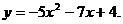
11. 
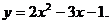
12. 
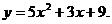
13. 
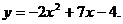
14. 
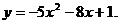
15. 
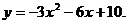
16. 
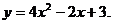
17. 
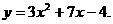
18. 
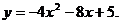
19. 
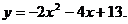
20. 
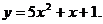
21. 
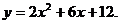
22. 
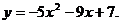
23. 
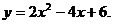
24. 
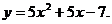
25. 
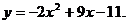
26. 
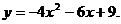
27. 
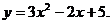
28. 
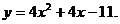
29. 
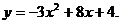
30. 
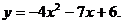
Задание 3. Вычислить пределы функции.
1. 
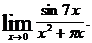
2. 
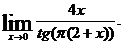
3. 
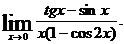
4. 
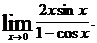
5. 
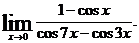
6. 
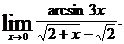
7. 
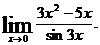
8. 
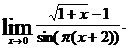
9. 
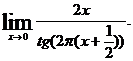
10. 
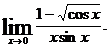
11. 
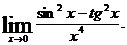
12. 
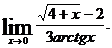
13. 
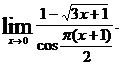
14. 
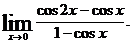
15. 
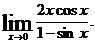
16. 
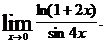
17. 
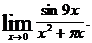
18. 
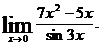
19. 
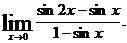
20. 
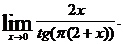
21. 
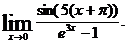
22. 
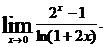
23. 
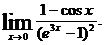
24. 
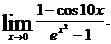
25. 
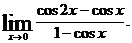
26. 
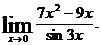
27. 
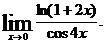
28. 
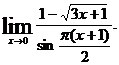
29. 
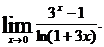
30. 