Тема №1 «Элементы теории множеств»
Цель: усвоить понятия множества, его элементов, конечного и бесконечного, равных множеств, научиться проводить основные операции над множествами.
Краткие теоретические сведения:
Множество – одно из основных неопределяемых понятий математики. Множество – совокупность объектов, обладающих одним и тем же признаком, объекты, не входящие в эту совокупность таким признаком не обладают. Объекты множества называются его элементами.
Множества обозначаются большими латинскими буквами, его элементы - маленькими.
Универсальное множество 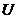 (универсум) – множество, которому принадлежат все те элементы, которые допустимо рассматривать при решении данной задачи.
(универсум) – множество, которому принадлежат все те элементы, которые допустимо рассматривать при решении данной задачи.
Пустое множествоØ–множество, которое не содержит ни одного элемента.
Способы задания множеств:
1) перечислением элементов – 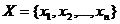 ,
,
2) указанием характеристического свойства – 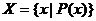 .
.
Если множество содержит конечное число элементов, то оно называется конечным, иначе множество называется бесконечным.
Если каждый элемент множества  является элементом множества
является элементом множества 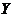 , то множество
, то множество  называется подмножеством множества
называется подмножеством множества 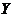 :
: 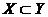 .
.
Свойства подмножеств:
1) 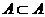 ,
,
2) Ø 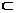
 .
.
Множества  и
и  называются равными, если они состоят из одних и тех же элементов:
называются равными, если они состоят из одних и тех же элементов: 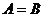 .
.
Всякое подмножество  данного множества
данного множества  , которое не совпадает с
, которое не совпадает с  и Ø, называется собственным подмножеством
и Ø, называется собственным подмножеством  .
.
Объединениеммножеств  и
и  называется множество
называется множество 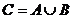 , состоящее из элементов множеств
, состоящее из элементов множеств  и
и  .
.
Пересечениеммножеств  и
и  называется множество
называется множество 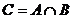 , состоящее из элементов, одновременно принадлежащих множеству
, состоящее из элементов, одновременно принадлежащих множеству  и множеству
и множеству  .
.
Разностью множеств  и
и  называется множество
называется множество 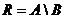 , состоящее из элементов
, состоящее из элементов  , которых нет в
, которых нет в  .
.
Геометрически операции над множествами изображаются с помощью диаграмм Эйлера – Венна:

 U
U 
 ∩
∩ 
 \
\ 
Свойства операций над множествами:
1) 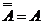 ,
,
2) 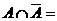 Ø,
Ø,
3) 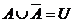 ,
,
4) 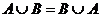 ,
, 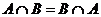 - коммутативность,
- коммутативность,
5) 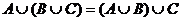 ,
, 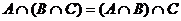 - ассоциативность,
- ассоциативность,
6) 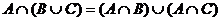 ,
, 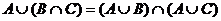 - дистрибутивность,
- дистрибутивность,
7) 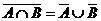 ,
, 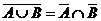 - законы де Моргана,
- законы де Моргана,
8) 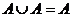 ,
, 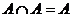 ,
,
9) 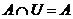 ,
, 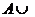 Ø
Ø 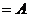 ,
,
10) 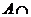 Ø = Ø,
Ø = Ø, 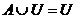 ,
,
11) 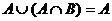 ,
, 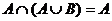 - законы поглощения.
- законы поглощения.
Пример. Доказать свойство 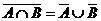 .
.
Решение. Пусть 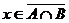 , тогда
, тогда 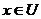 и
и 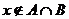 , то есть либо
, то есть либо 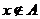 , либо
, либо 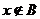 . В первом случае
. В первом случае 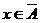 , но тогда
, но тогда 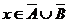 ; во втором случае
; во втором случае 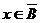 , но тогда
, но тогда 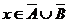 . Следовательно,
. Следовательно, 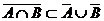 .
.
Пусть 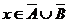 , тогда либо
, тогда либо 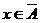 , либо
, либо 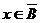 . В первом случае
. В первом случае 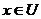 и
и 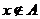 , тогда
, тогда 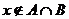 и
и 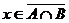 ; во втором случае
; во втором случае 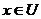 и
и 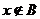 , но тогда
, но тогда 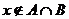 и
и 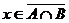 . Следовательно,
. Следовательно, 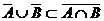 .
.
Так как 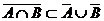 и
и 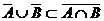 , то
, то 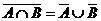 .
.
Множество, рассматриваемое вместе с каким-нибудь установленным в нём порядком следования элементов, называется упорядоченным множеством.
Основные числовые множества:
1) 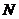 – натуральные,
– натуральные,
2) 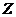 – целые,
– целые,
3) 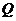 - рациональные,
- рациональные,
4) 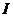 – иррациональные,
– иррациональные,
5) 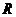 – действительные,
– действительные,
6) 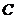 – комплексные числа.
– комплексные числа.
Между множествами  и
и 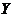 установлено соответствие, если по какому-либо закону или правилу каждому элементу множества
установлено соответствие, если по какому-либо закону или правилу каждому элементу множества  соответствует элемент множества
соответствует элемент множества 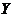 . Соответствие называется взаимно-однозначным, если любому элементу из
. Соответствие называется взаимно-однозначным, если любому элементу из  соответствует только один элемент из
соответствует только один элемент из 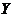 и наоборот. Два множества называются эквивалентными,если между их элементами установлено взаимно-однозначное соответствие:
и наоборот. Два множества называются эквивалентными,если между их элементами установлено взаимно-однозначное соответствие:  ~
~ 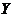 .
.
Если множества эквивалентны, то они имеют одинаковую мощность или кардинальное число 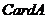 .
.
Мощность конечного множества равна числу элементов этого множества. Мощность пустого множества равна нулю.
Бесконечное множество называется счётным, если оно эквивалентно множеству натуральных чисел. Бесконечное множество, мощность которого превышает мощность счётного множества, называется несчётным.
Множество действительных чисел несчётно и его мощность называется мощностью континуума.
Пусть имеются два множества  и
и  . Прямое (декартово) произведение
. Прямое (декартово) произведение 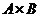 есть множество всех упорядоченных пар
есть множество всех упорядоченных пар 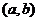 , в которых первый элемент принадлежит множеству
, в которых первый элемент принадлежит множеству  , а второй – множеству
, а второй – множеству  .
.
Пример. Пусть 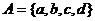 ,
, 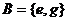 . Тогда
. Тогда
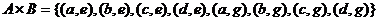 .
.
Нечётким множеством  в универсальном множестве
в универсальном множестве 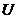 называется совокупность упорядоченных пар
называется совокупность упорядоченных пар 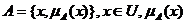 – степень принадлежности
– степень принадлежности 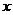 множеству
множеству  .
.
Пример. Математико-психологический портрет группы студентов 1-го курса факультета клинической психологии по степени принадлежности каждого из них к множеству трудолюбивых людей.
| Студенты | Антонова | Веркутов | Любимова | Миронова | Новиков | Калинина | Осина |
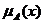 | 0,8 | 0,7 | 0,4 | 0,9 | 0,3 | 0,5 | 0,4 |
Объединениемнечётких множеств  и
и  называется нечёткое множество
называется нечёткое множество 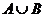 с функцией принадлежности
с функцией принадлежности 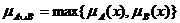 .
.
Пересечениемнечётких множеств  и
и  называется нечёткое множество
называется нечёткое множество 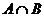 с функцией принадлежности
с функцией принадлежности 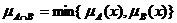 .
.
Лингвистическая переменная – переменная, значениями которой являются слова или предложения естественного или искусственного языков.
Контрольные вопросы:
1. Понятие множества и его элементов. Способы задания множеств.
2. Конечное и бесконечное множества.
3. Подмножество. Свойства подмножеств.
4. Операции над множествами.
5. Основные числовые множества.
6. Мощность множества. Счётное и несчётное множества.
7. Декартово произведение множеств.
8. Нечёткие множества. Пример.
9. Операции над нечёткими множествами.
10. Понятие лингвистической переменной.
Контрольные задания:
1. Определить является ли одно из множеств 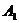 и
и 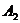 собственным подмножеством другого:
собственным подмножеством другого:
а) 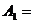 {1,{1,2}},
{1,{1,2}}, 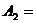 {{1,2},2},
{{1,2},2},
б) 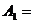 {1},
{1}, 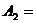 {1,{1}}.
{1,{1}}.
2. Какие из элементов множества  одновременно являются и его подмножествами:
одновременно являются и его подмножествами: 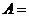 {Ø,{Ø},{1}}?
{Ø,{Ø},{1}}?
3. Для двухэлементного множества  построить
построить  - множество всех подмножеств
- множество всех подмножеств  :
:  ={1,2}.
={1,2}.
4. Найти объединение, пересечение, разность и декартово произведение множеств  и
и  :
:
а)  и
и  – множества всех букв слов «параллельность» и «трапеция»,
– множества всех букв слов «параллельность» и «трапеция»,
б)  и
и  – множества всех цифр чисел 3464675678 и 3464758858.
– множества всех цифр чисел 3464675678 и 3464758858.
5. Найти объединение, пересечение и разность следующих промежутков:
а) [3;7), (4;9],
б) (- 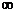 ;5], (0;+
;5], (0;+ 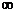 ),
),
в) [1;10], (-7;4].
6. Доказать и с помощью диаграмм Эйлера-Венна проверить:
а)  \
\  =
=  \(
\( 
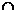
 ),
),
б)  \
\  = (
= ( 
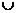
 )\
)\  ,
,
в) ( 
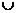
 )\
)\ 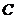 = (
= (  \
\ 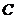 )
) 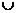 (
(  \
\ 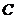 ),
),
г) (  \
\ 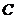 )
) 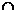 (
(  \
\ 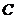 ) = (
) = ( 
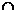
 )\
)\ 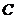 .
.
7. Решить задачу:
Из 32 учеников класса 12 занимаются в волейбольной секции, 15 – в баскетбольной, 8 – и в той, и в другой. Сколько школьников не занимаются ни в волейбольной, ни в баскетбольной секциях.
Задания для домашней работы:
1. Найти объединение, пересечение, разность и декартово произведение множеств  и
и  :
:
а)  и
и  – множества всех букв слов «алгебра» и «планета»,
– множества всех букв слов «алгебра» и «планета»,
б)  и
и  – множества всех цифр чисел 5660399839 и 5382388992.
– множества всех цифр чисел 5660399839 и 5382388992.
2. Доказать и с помощью диаграмм Эйлера-Венна проверить:
а) (  \
\  )\
)\ 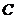 =
=  \(
\( 
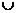
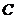 ),
),
б)  \(
\(  \
\ 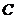 ) = (
) = (  \
\  )
) 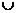 (
( 
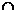
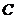 ),
),
в) (  \
\  )
) 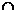 (
( 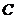 \
\ 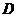 ) = (
) = ( 
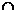
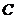 )\(
)\( 
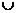
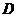 ).
).
3. Найти объединение, пересечение и разность следующих промежутков:
а) (-1;3), [2;+ 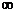 ),
),
б) [1;4), [2;3],
в) [1;3), [5; + 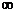 ).
).
