Тригонометрическая подстановка

Интегралы вида

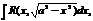
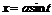
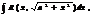
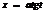
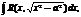
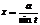
с помощью замен сводятся к интегралам от рац. ф-ий.

«Берущиеся» и «не берущиеся» интегралы

Говорят, что интеграл берется или вычисляется, если первообр. выражается через элементарные ф-и. Если же первообр. не вычисляется, то говорят, что интеграл не берется.

Пример: 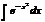- интеграл Пуассона (теория вероятности)

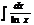-интегральный логарифм (теория чисел)

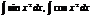-интегралы Френеля (физика)

Первообразные этих ф-ий хорошо изучены, для них составлены подробные таблицы для различных значений аргумента х.

Дифференциальные ур-ния.

ДУ наз-тся соотношение, связывающее независимую переменную 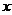, искомую ф. 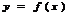и ее производную. Если искомая ф. есть ф-я одной независимой переменной, то ДУ наз-тсяобыкновенным. Порядок старшей производной, входящей в ДУ наз-тся порядком данногоур-ния.

Общий вид ДУ 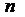–ного порядка .

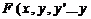Пр. –ДУ 1-го порядка.

ДУ. Линейные ДУ 1 порядка.

Дифференциальным уравнением наз соотношение, связывающее независ переменную x, искомую ф-июy=f(x) и её производную.

Если искомая функция есть ф-ия одной независимой переменной, то ДУ наз обыкновенным, порядок старшей производной , входящей в ДУ, наз порядком ланногоур-я.

Общий вид ДУ n-го порядка: 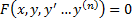(1)

Ф-ияy=f(x), кот-я при подстановке в ур-е (1) обращает этоур-е в тождество, наз-ся решением этого ур-я.

ДУ 1-го порядка имеет вид: F(x,y,y’)=0 (2) или y’=f(x,y)(3) в случае, если y’ можно выразить относительно x и y

Реш-е ур-я (3) наз-ся общим реш-ем этого ур-я.

Реш-е может получаться в неявной форме Ф(x,y,c)=0 – наз общим интегралом.

Реш-е, кот получается из общего при некотором фиксированном значении С наз частным решением. Условия, что при x=x₀ ф-ияy=y₀наз начальным условием, кот-е позволяет из общего реш-я выделить частное.

Ур-я с разделяющимися переменными.

Ур-е вида наз ур-ем с разделяющимися переменными. Это ур-е можно записать в виде:

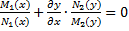, домножим на :

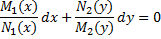
Вычислим: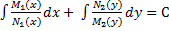

Однородные ДУ

Ф-ияf(x,y) наз однородной измерения М если имеет место тождество f(xt,yt)=t^m(x,y)

f(x,y) = x²-3xy+2y²

f(tx,ty)=(tx)²-3(tx)(ty)+2(ty)²=t²(x²-3xy+2y²)=t²f(x,y) – однородная ф-ия измерения t.

Ур-е M(x,y)dx+N(x,y)dy=0 наз однородным ДУ 1-го порядка, если ф-ииM и N однородные ф-ии одного и того же измерения.

С помощью подстановки y=ux, где u – искомая ф-ия, зависящая от x, ур-е сводится к ур-ю с разделяющимися переменными.

Линейные ДУ 1-го порядка: Ур-е вида y’+p(x)y=q(x)

Для реш-я исп-ют подстановку y=uv; dy=vdu+udv

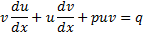
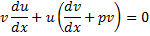
Ф-ию 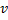подбирают т.о., чтобы 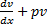=0.

Метод Лагранжа.

Линейное ДУ 1-го порядка наз линейным если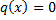

Y’+py=0

Для ур-й 1-го порядка это ур-е с разделяющимися переменными. Метод Лагранжа заключается в следующем: сначала мы решаем соответственно однородноеур-е, полученная ф-ия содержит С. Для реш-я исходного ур-я подбираем С т.о., чтобы реш-е однородного ур-я давало реш-е исходного, считая С зависящей от x.

19))Числовые и функциональные ряды.

Числовые ряды.

Числовой ряд-символ, обозначаемый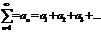

Числа 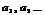наз-ют членами этого ряда.

Суммы конечного числа членов этого ряда 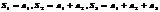наз-ют частичными суммами или отрезками данного ряда.

Рассм. послед-сть 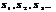. Если сущ-ет 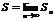, то ряд наз-ют сходящимся, число 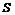–суммой этого ряда. Если послед-сть 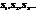не имеет предела, то ряд расходящийся.

Пр. , ,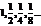

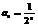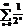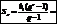
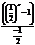
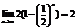след-но данный числовой ряд сходится и его сумма =0.

Св-ва числовых рядов:

1) если из членов ряда отбросить 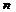первых членов, то получим ряд 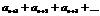, к-рыйназ-тся 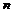–ным остатком. Остаток данного ряда сходится и расходится одновременно с исходным рядом. Это означает, что при исследовании сходимости ряда можно отбрасывать конечное число первых членов.

2) (необходимый признак сходимости). Общий член сходящегося ряда ®0, т.е. 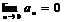, что не явл. достаточным признаком.

3) если ряд 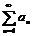сходится и его сумма = 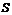, то ряд 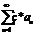также сходится, и его сумма =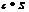

4) если 2 числовых ряда 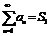и 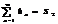сходятся, тогда ряд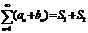

Положительные ряды.

Полож. рядом наз-тся ряд, члены к-рогонеотриц.

1. Признак сравнения.

Пусть даны 2 «+» ряда 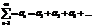(1) и 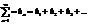(2) начиная с нек-рого номера 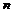вып-тся условие 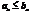, тогда из сходимости ряда (2) следует сходимость ряда (1), а из расходимости ряда (1) следует расходимость ряда (2).

2. Признак Даламбера.

Если члены «+» -ного ряда 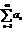таковы, что сущ-ет предел 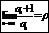, тогда если r<1 -ряд сходится; r>1 - расходится; r=1 -нужны доп. исследования.

Интегральный признак Коши.

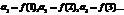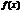Пусть члены «+» ряда таковы, что , где при 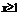непрерывн., «+» и убывает, тогда исх. ряд 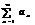и несобств. интеграл 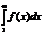сходятся и расходятся одновременно.

Пр. 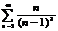рассм. соотв. несобств. интеграл 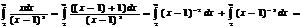= 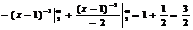- ряд сходится.

Знакочередующиеся ряды.

Знакочеред. рядом наз-тся ряд вида , где . Этот ряд можно записать в виде

Признак Лейбница.

Если члены знакочеред. ряда удовлетворяют условиям:

1.

2.

то знакочеред. ряд сходится.

Абсолютная и условная сходимость.

О. Ряд (1) наз-тсяабсолютно сходящимся, если сходится ряд (2). Если же ряд (1), а ряд (2) расх., то такие ряды наз-ют условно сходящимися. 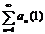и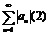

Теорема:если ряд сходится абсолютно, то он сходится.

Пр. 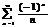-ряд Лейбница сходится. 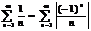-гармонич. ряд расходится.

т.е. данный пример пок-ет, что сущ-ют ряды сходящиеся, но не сходящиеся абсолютно.

Если ряд с произвольными членами расходится, то члены данного ряда можно расставить таким образом, что ряд будет сходиться к любому наперед заданному числу.

Функциональные ряды.

Ряды, членами к-рыхявл. функции наз-тсяфункциональным рядом.

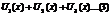
Если вместо переменной положить 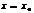, где 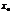–из обл. определения ф-и 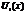, то получим числовой ряд 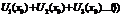. Если данный ряд сходится, то наз. точкой сходимости, если числ. ряд расходится. то 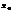–точка расходимости.

О. Совокупность всех точек сходимости функ. ряда наз-тся областью его сходимости.

Пр. 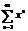при 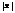<1 ряд сходится, а при 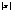>1 ряд расходится.

Рассм. соотв. числовые ряды пр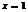и и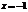

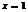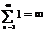: -расходится

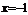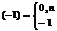: след-но обл. сходимости (-1;1).

Степенные ряды.

-функциональный ряд вида 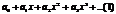, где 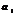–действит. числа, называемые коэф-тами степенного ряда.

1. если степенной ряд сходится только в т. 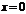, то его будем относить к рядам 1-го класса.

Пр. 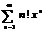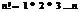. Применим признак Даламбера

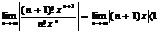
т.к. 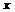–конечно, то данный предел при 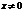, остается единственный случай, когда 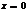– ряд-1-го рода.

2. ряд (1) сходящийся в любой точке, будем относить к рядам 2-го рода.

Пр.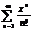

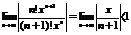
т.к. 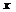– конечная точка на числ. прямой, то данный предел при любом 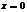, след-но при любом 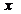по признаку Даламбера ряд сходится-ряд 2-го рода.

3. ряд, не Î к 1-му и 2-му классу относят к рядам 3-го класса.

Пр. 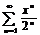т.к. при 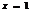ряд сходится, то ряд не относится к 1-му классу, т.к. при 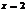ряд расходится, то ряд не относится ко 2-му ряду, т.е. это ряд 3-го класса.

Теорема Авеля: если степенной ряд (1) сходится при 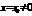, то он абсолютно сходится для любого 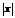< 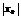. Если же степ.ряд (1) расходится при 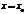, то он расходится и при всех > .

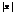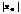След-но для каждого степенного ряда(1) третьего класса сущ-ет число 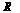>0, называемое радиусом сходимости, для к-роговып-тся условия: при 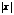< 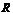ряд сходится абсолютно , при 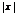> 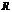–расходится. Промежуток 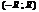наз-тся интервалом сходимости степ.ряда. Для степ. ряда 2-го класса инт. сходимости (-¥;+¥). Областью сходимости степ.ряда явл. интервал, к-рому в отдельном случае добавляются один или оба конца этого интервала. Для степенного ряда 1-го класса полагают 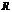=0, 2-го класса =¥.

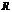Теорема. Пусть для степенного ряда сущ-ет и оличен от 0 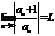, тогда .

Пр.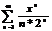

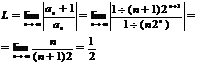
тогда 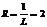. Проверим как ведет себя ряд на границе сходимости

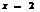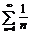: -расходится(гармонич. ряд)

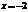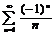: - ряд Лейбница (сходится). След-но область сходимости .

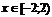ДУ второго порядка

Общий вид: F(x,y,y’,y’’)=0. Общее реш-е содержит 2 независимые произвольные постоянные с₁ и с₂. Если заданы начальные условия y(x₀)=y₀, y’(x₀) = y’₀, то из с-мы 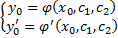можно найти произв постоянные с₁ и с₂, тем самым найти частное реш-е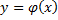

Ур-я 2-го порядка решаются путём применения неопределённого интегрирования в след случаях:

1. Пусть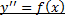

; ; ;

;

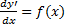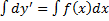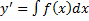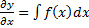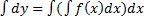
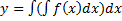+c

2.

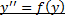
Положим 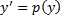, тогда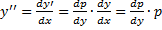

=>данноеур-е примет вид: 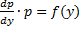, те получаем ур-е 1-го порядка с разделяющимися переменными.

Однородные линейные ДУ 2-го порядка имеет вид: 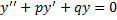;p,q – нек действительные числа.

Искать решение в виде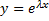

λ²+pλ+q=0 – характеристическое ур-е.

1 случай:ур-е имеет 2 действит корня, λ₁≠ λ₂, тогда общее реш-е имеет вид: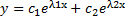

2 случай: ур-е имеет 2 действитсовп корня λ₁= λ₂= λ

Общее реш-е: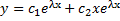

3 случай: корни квадратногоур-я мнимые: λ_1,2= ,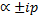

Общий вид:

Линейные неоднородные ДУ 2-го порядка с постоянными коэффициентами: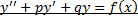

Т. Общее реш-е неоднородного ЛДУ 2-го порядка с пост коээф-ми равно 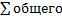решения соответствующего однородного ур-я и частноо реш-я исходного неоднородного ур-я.

Нахождение частного реш-я неоднородного ур-я:

1. Пусть правая часть – показательная ф-ия,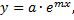

a≠0:

а) m не явл корнем характеристического многочлена, тогда частное реш-е в виде: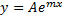

б) если характеристическое ур-е имеет 2 разл действ корня, один из кот-х = m, то частное реш-е в виде: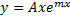

в) если корни характеристическогоур-я совпадают и равны m, то частное реш-е в виде: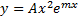

2. Правая часть неоднородногоур-я – тригонометрическая ф-ия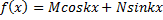

Частное реш-е в случае, когда ± ki не явл-ся корнем характеристическогоур-я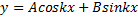

Если же kiявл корнем хар-гоур-я, то частное реш-е в виде: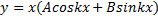

3. Правая часть линейногоур-я предст собой многочлен P_n(x), тогда частное реш-е в случае коглаq≠0 будем искать в виде Q_n(x)

Если q=0, p≠0, тогда в виде xQ_n(x).