Матрица как запись коэффициентов системы линейных уравнений

Систему из 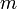линейных уравнений с 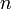неизвестными

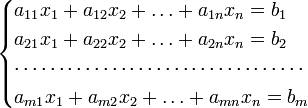
можно представить в матричном виде

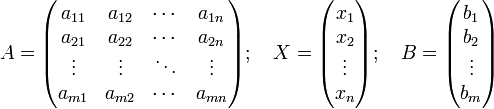
и тогда всю систему линейных уравнений можно записать так:

,

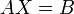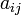где имеет смысл таблицы коэффициентов системы линейных уравнений.

Если 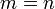и матрица невырожденная, то решение этого уравнения состоит в нахождении обратной матрицы 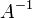, поскольку умножив обе части уравнения на эту матрицу слева

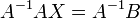
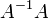— превращается в 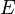(единичную матрицу). И это даёт возможность получить столбец корней уравнений

.

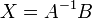Все правила, по которым проводятся операции над матрицами, выводятся из операций над системами уравнений.

Квадратная матрица и смежные определения

Если количество строк матрицы равно количеству столбцов, то такая матрица называется квадратной.

Для квадратных матриц существует единичная матрица 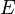(аналог единицы для операции умножения чисел) такая, что умножение любой матрицы на неё не влияет на результат, а именно

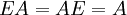
У единичной матрицы единицы стоят только по главной диагонали, остальные элементы равны нулю

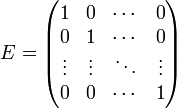
Для некоторых квадратных матриц можно найти так называемую обратную матрицу. Обратная матрица 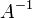такова, что если матрицу умножить на обратную ей матрицу, то получится единичная матрица:

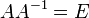
Обратная матрица существует не всегда. Матрицы, для которых обратная матрица существует, называются невырожденными (или регулярными), а для которых нет — вырожденными (или сингулярными). Матрица невырождена, если все ее строки (столбцы) линейно независимы как векторы. Максимальное число линейно независимых строк (столбцов) называется рангом матрицы. Определителем (детерминантом) матрицы называется значение нормированной кососимметрической (антисимметрической) полилинейной формы валентности 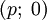на столбцах матрицы. Квадратная матрица над числовым полем вырождена тогда и только тогда, когда ее определитель равен нулю.

Элементарные преобразования матриц

Основная статья: Элементарные преобразования матрицы

Элементарными преобразованиями строк матрицы называются следующие преобразования:

1. Умножение строки на число отличное от нуля,
2. Прибавление одной строки, умноженной на число, к другой строке,
3. Перестановка местами двух строк.

Элементарные преобразование столбцов матрицы определяются аналогично. При элементарных преобразованиях ранг матрицы не меняется.

Матрица линейного оператора

Матрица линейного оператора — матрица, выражающая линейный оператор в некотором базисе. Для того, чтобы ее получить, необходимо подействовать оператором на векторы базиса и координаты полученных векторов (образов базисных векторов) записать в столбцы матрицы.

Матрица оператора аналогична координатам вектора. При этом действие оператора на вектор равносильно умножению матрицы на столбец координат этого вектора в том же базисе.

Выберем базис 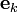. Пусть 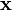— произвольный вектор. Тогда его можно разложить по этому базису:

,

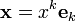где 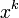— координаты вектора 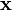в выбранном базисе.

Здесь и далее предполагается суммирование по немым индексам.

Пусть 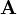— произвольный линейный оператор. Подействуем им на обе стороны предыдущего равенства, получим

.

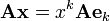Вектора 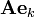также разложим в выбранном базисе, получим

,

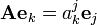где 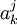— 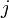-я координата 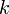-го вектора из .

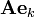Подставим разложение в предыдущую формулу, получим

.

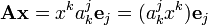Выражение 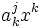, заключённое в скобки, есть ни что иное, как формула умножения матрицы на столбец, и, таким образом, матрица 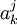при умножении на столбец 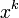даёт в результате координаты вектора 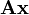, возникшего от действия оператора 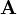на вектор 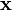, что и требовалось получить.

Комментарий: Если в полученной матрице поменять местами пару столбцов или строк, то мы, вообще говоря, получим уже другую матрицу, соответствующую тому же набору базисных элементов 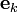. Иными словами, порядок базисных элементов предполагается жёстко упорядоченным.

Матрицы в теории групп

Матрицы играют важную роль в теории групп. Они используются при построении общих линейных групп, специальных линейных групп, диагональных групп, треугольных групп, унитреугольных групп.

Конечную группу (в частности, симметрическую) можно (изоморфно) промоделировать матрицами перестановок (содержащими только "0" и "1"),

например, для : , , , , , .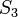

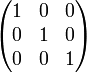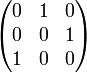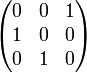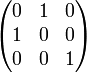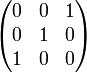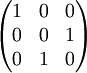Поле 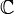комплексных чисел может быть (изоморфно) промоделировано над полем 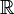вещественных чисел:

для 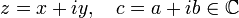матричные аналоги 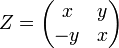, , 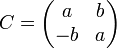где ;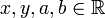

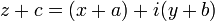соответствует ;

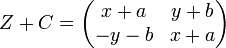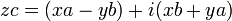соответствует ;

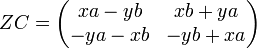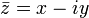соответствует ;

;

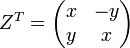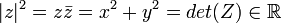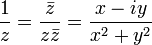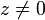при соответствует 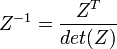при ;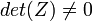

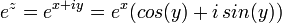соответствует .

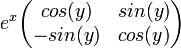В частности, для ,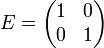

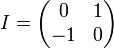
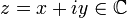соответствует ,

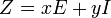где .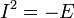

Замечание. Модель имеет автоморфизм 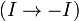, т.е.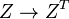

Тело кватернионов 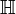может быть (изоморфно) промоделировано над полем 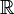вещественных чисел:

для 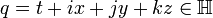матричный аналог 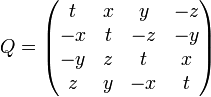, где .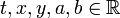

Для того, чтобы кватерниону 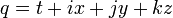соответствовала матрица ,

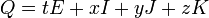где , , , ,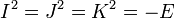

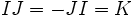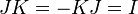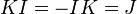можно ввести базисные элементы

, , , .

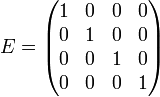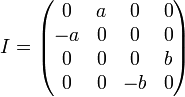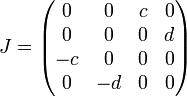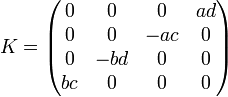Параметры должны удовлетворять условиям: 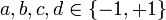и .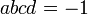

Существует 8 решений (8 представлений).

См. также

• Норма матрицы
• Определитель матрицы
• Собственные векторы, значения и пространства
• Массив — тип данных в программировании, соответствующий матрице (многомерность достигается вложенными массивами).
• Разрежённый массив — компьютерная форма представления матриц со множеством нулей.
• Линейные матричные неравенства — аппарат для решения задач синтеза законов управления.
• Лямбда-матрица
• Жорданова нормальная форма
• Список матриц

Примечания

1. ↑ Под треугольными матрицами сейчас понимают матрицы, ненулевые элементы которых заполняют в таблице матрицы треугольную область, остальные же элементы - нули.
2. ↑ Этот изоморфизм полностью задается выбором базиса в линейном пространстве: при фиксированном базисе изоморфизм фиксирован и таким образом реализована взаимная однозначность соответствия матриц операторам. Это не означает того, что такой изоморфизм в принципе единственный: в другом базисе тем же линейным операторам будут соответствовать другие матрицы (тоже взаимно однозначно при фиксации этого нового базиса).
3. ↑ Даан-Дальмедико А., Пейффер Ж. Пути и лабиринты. Очерки по истории математики: Пер. с франц. — М.: Мир, 1986. — С. 397.
4. ↑ Формально в этом определении всё симметрично, и можно было бы поменять "основной" и дуальный базис местами (они оба просто взаимно дуальны), однако принято именно описанное соглашение.