Вектор-строка и вектор-столбец
История
Впервые матрицы упоминались ещё в древнем Китае, называясь тогда «волшебным квадратом». Основным применением матриц было решение линейных уравнений. Также волшебные квадраты были известны чуть позднее у арабских математиков, примерно тогда появился принцип сложения матриц. После развития теории определителей в конце 17-го века, Габриэль Крамер начал разрабатывать свою теорию в 18-ом столетии и опубликовал «правило Крамера» в 1751 году. Примерно в этом же промежутке времени появился «метод Гаусса». Теория матриц начала своё существование в середине XIX века в работах Уильяма Гамильтона и Артура Кэли. Фундаментальные результаты в теории матриц принадлежат Вейерштрассу, Жордану, Фробениусу. Термин «матрица» ввел Джеймс Сильвестр в 1850 г.[3]
Определение
Пусть есть два конечных множества 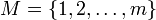 и
и 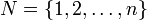 , где
, где 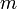 и
и 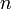 - натуральные числа.
- натуральные числа.
Назовём матрицей размера 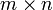 (читается
(читается 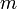 на
на 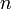 ) с элементами из некоторого кольца или поля
) с элементами из некоторого кольца или поля 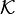 отображение вида
отображение вида
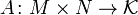 .
.
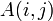 называется элементом матрицы, находящимся на пересечении
называется элементом матрицы, находящимся на пересечении 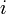 -той строки и
-той строки и 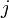 -ого столбца;
-ого столбца;
-
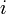 -ая строка матрицы состоит из элементов вида
-ая строка матрицы состоит из элементов вида 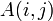 , где
, где 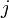 пробегает всё множество
пробегает всё множество 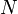 ;
; -
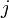 -ый столбец матрицы состоит из элементов вида
-ый столбец матрицы состоит из элементов вида 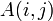 , где
, где 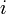 пробегает всё множество
пробегает всё множество 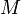 .
.
Если индекс 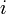 пробегает множество
пробегает множество 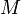 , а
, а 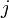 пробегает множество
пробегает множество 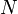 , то совокупность элементов
, то совокупность элементов 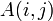 полностью определяет матрицу.
полностью определяет матрицу.
Таким образом, матрица размера 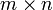 состоит в точности из
состоит в точности из
-
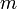 строк (по
строк (по 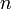 элементов в каждом)
элементов в каждом) - и
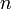 столбцов (по
столбцов (по 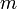 элементов в каждом)
элементов в каждом) - или
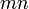 элементов.
элементов.
В соответствии с этим
- каждую строку матрицы можно интерпретировать как вектор в
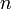 -мерном координатном пространстве
-мерном координатном пространстве 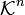 ;
; - каждый столбец матрицы — как вектор в
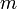 -мерном координатном пространстве
-мерном координатном пространстве 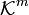 .
.
Сама матрица естественным образом интерпретируется как вектор в пространстве 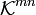 , имеющем размерность
, имеющем размерность 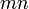 . Это позволяет ввести покомпонентное сложение матриц и умножение матрицы на число (см. ниже); что касается матричного умножения, то оно существенным образом опирается на прямоугольную структуру матрицы.
. Это позволяет ввести покомпонентное сложение матриц и умножение матрицы на число (см. ниже); что касается матричного умножения, то оно существенным образом опирается на прямоугольную структуру матрицы.
Если у матрицы количество строк 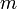 совпадает с количеством столбцов
совпадает с количеством столбцов 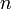 , то такая матрица называется квадратной, а число
, то такая матрица называется квадратной, а число 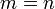 называется размером квадратной матрицы или её порядком.
называется размером квадратной матрицы или её порядком.
Обозначения
Обычно матрицу обозначают заглавной буквой латинского алфавита: пусть
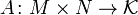 ,
,
тогда  — матрица, которая интерпретируется как прямоугольный массив элементов поля
— матрица, которая интерпретируется как прямоугольный массив элементов поля 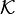 вида
вида 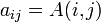 , где
, где
- первый индекс означает индекс строки:
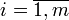 ;
; - второй индекс означает индекс столбца:
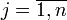 ;
;
таким образом, 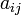 — элемент матрицы
— элемент матрицы  , находящийся на пересечении
, находящийся на пересечении 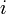 -той строки и
-той строки и 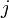 -того столбца. В соответствии с этим принято следующее компактное обозначение для матрицы размера
-того столбца. В соответствии с этим принято следующее компактное обозначение для матрицы размера 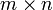 :
:
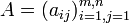
или просто:
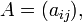
если нужно просто указать обозначение для элементов матрицы.
Иногда, вместо 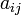 , пишут
, пишут 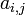 , чтобы отделить индексы друг от друга и избежать смешения с произведением двух чисел.
, чтобы отделить индексы друг от друга и избежать смешения с произведением двух чисел.
Если необходимо дать развёрнутое представление матрицы в виде таблицы, то используют запись вида

Можно встретить как обозначения с круглыми скобками «(…)», так и обозначения с квадратными скобками «[…]». Реже можно встретить обозначения с двойными прямыми линиями "||…||").
Поскольку матрица состоит из строк и столбцов, для них используются следующие обозначения:
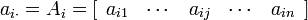 — это
— это 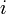 -тая строка матрицы
-тая строка матрицы  ,
,
а
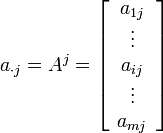 — это
— это 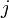 -тый столбец матрицы
-тый столбец матрицы  .
.
Таким образом, матрица обладает двойственным представлением — по строкам:
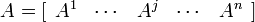
и по столбцам:
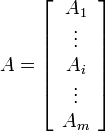 .
.
Такое представление позволяет формулировать свойства матриц в терминах строк или в терминах столбцов.
Транспонированная матрица
С каждой матрицей 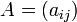 размера
размера 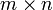 связана матрица
связана матрица 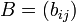 размера
размера 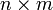 вида
вида
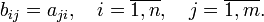
Такая матрица называется транспонированной матрицей для  и обозначается так
и обозначается так 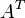 .
.
Транспонированную матрицу можно получить, поменяв строки и столбцы матрицы местами. Матрица 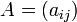 размера
размера 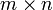 при этом преобразовании станет матрицей размерностью
при этом преобразовании станет матрицей размерностью 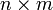 .
.
Диагональная матрица
Диагональная матрица - квадратная матрица, все элементы которой кроме диагональных - нулевые 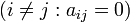 , иногда записывается как
, иногда записывается как
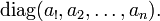
Единичная матрица
Единичная матрица - матрица, при умножении на которую любая матрица (или вектор) остается неизменной, является диагональной матрицей с единичными (всеми) диагональными элементами:
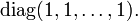
Для ее обозначения чаще всего используется обозначение I или E, а также просто 1 (или 1 специальным шрифтом).
Для обозначения ее элементов также используется символ Кронекера 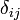 , определяемый как:
, определяемый как:
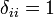
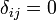 при
при 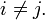
Нулевая матрица
Для обозначения нулевой матрицы - матрицы, все элементы которой нули (при сложении ее с любой матрицей та остается неизменной, а при умножении на любую получается нулевая матрица) - используется обычно просто 0 или 0 специальным шрифтом, или буква, начертанием похожая на ноль, например 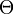 .
.
Операции над матрицами
Умножение матрицы на число
Умножение матрицы  на число
на число 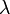 (обозначение:
(обозначение: 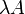 ) заключается в построении матрицы
) заключается в построении матрицы 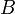 , элементы которой получены путём умножения каждого элемента матрицы
, элементы которой получены путём умножения каждого элемента матрицы  на это число, то есть каждый элемент матрицы
на это число, то есть каждый элемент матрицы 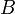 равен
равен
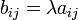
Свойства умножения матриц на число:
- 1. 1A = A;
- 2. (λβ)A = λ(βA)
- 3. (λ+β)A = λA + βA
- 4. λ(A+B) = λA + λB
Сложение матриц
Сложение матриц 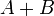 есть операция нахождения матрицы
есть операция нахождения матрицы 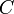 , все элементы которой равны попарной сумме всех соответствующих элементов матриц
, все элементы которой равны попарной сумме всех соответствующих элементов матриц  и
и 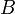 , то есть каждый элемент матрицы
, то есть каждый элемент матрицы 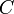 равен
равен
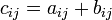
Свойства сложения матриц:
- 1.коммутативность: A+B = B+A;
- 2.ассоциативность: (A+B)+C =A+(B+C);
- 3.сложение с нулевой матрицей: A + Θ = A;
- 4.существование противоположной матрицы: A + (-A) = Θ;
Все свойства линейных операций повторяют аксиомы линейного пространства и поэтому справедлива теорема:
Множество всех матриц одинаковых размеров mxn с элементами из поля P (поля всех действительных или комплексных чисел) образуют линейное пространство над полем P (каждая такая матрица является вектором этого пространства). Впрочем, прежде всего во избежание терминологической путаницы, матрицы в обычных контекстах избегают без необходимости (которой нет в наиболее обычных стандартных применениях) и четкого уточнения употребления термина называть векторами.
Умножение матриц
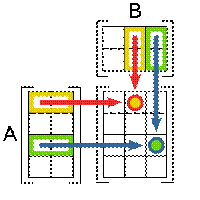
Умножение матриц (обозначение: 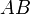 , реже со знаком умножения
, реже со знаком умножения 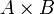 ) — есть операция вычисления матрицы
) — есть операция вычисления матрицы 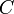 , элементы которой равны сумме произведений элементов в соответствующей строке первого множителя и столбце второго.
, элементы которой равны сумме произведений элементов в соответствующей строке первого множителя и столбце второго.
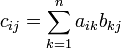
Количество столбцов в матрице  должно совпадать с количеством строк в матрице
должно совпадать с количеством строк в матрице 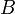 , иными словами, матрица
, иными словами, матрица  обязана быть согласованной с матрицей
обязана быть согласованной с матрицей 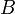 . Если матрица
. Если матрица  имеет размерность
имеет размерность 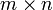 ,
, 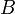 —
— 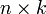 , то размерность их произведения
, то размерность их произведения 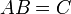 есть
есть 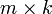 .
.
Свойства умножения матриц:
- 1.ассоциативность (AB)C = A(BC);
- 2.некоммутативность (в общем случае): AB
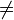 BA;
BA;
- 3.произведение коммутативно в случае умножения с единичной матрицей: AI = IA;
- 4.дистрибутивность: (A+B)C = AC + BC, A(B+C) = AB + AC;
- 5.ассоциативность и коммутативность относительно умножения на число: (λA)B = λ(AB) = A(λB);
Комплексное сопряжение
Если элементами матрицы 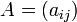 являются комплексные числа, то комплексно сопряжённая (не путать с эрмитово сопряжённой! см. далее) матрица равна
являются комплексные числа, то комплексно сопряжённая (не путать с эрмитово сопряжённой! см. далее) матрица равна 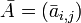 . Здесь
. Здесь 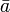 — число, комплексно сопряжённое к
— число, комплексно сопряжённое к 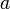 .
.
След
Основная статья: След матрицы
Для квадратной матрицы определен след:
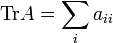
(иногда также обозначается как Sp или Spur).
Является инвариантом ортогональных (унитарных) преобразований матрицы, соответствующих преобразованию матричного представления линейного оператора или билинейной (квадратичной) формы при соотвестствующем преобразовании векторного пространства (например, вращении).
Определитель (детерминант)
Основная статья: Определитель
Перманент
Основная статья: Перманент
Линейные трансформации
Основные статьи: Линейная трансформация, Трансформация матрицы


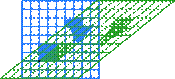
Векторы представлены как матрица 2 x 2, образованная сторонами соответствующего единичного квадрата, трансформируемого в параллелограмм.
Матрицы и их произведения выявляют их существенные особенности, когда это связано с линейными преобразованиями, так же известными, как линейные карты. Матрица A вещественных чисел размера m × n порождает линейное преобразование Rn → Rm отображая каждый вектор x в Rn на новую матрицу Ax, которая является вектором Rm. Наоборот, каждое линейное преобразование f: Rn → Rm вытекает из уникальной m × n матрицы A: явно (i, j)-вхождение матрицы A есть i-тая координата f(ej), где ej = (0,...,0,1,0,...,0) является единичным вектором с единицей в j-той позиции и 0 в остальных случаях. Матрица A как говорят, представляет собой линейную карту f, и называется матрицей трансформирования f.
Для примера матрица 2×2
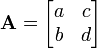
может быть рассмотрена при трансформации единичного квадрата в параллелограмм с вершинами (0, 0), (a, b), (a + c, b + d), и (c, d). Параллелограмм, показанный на рисунке справа получается путем умножения матрицы A на каждый вектор-столбец 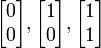 и
и  . Эти векторы определяют вершины единицы площади.
. Эти векторы определяют вершины единицы площади.
В следующей таблице показаны матрицы 2 × 2 вещественных чисел с соответствующими им линейными картами R2. Синим цветом обозначена исходная карта, а зеленым - трансформированная and shapes. Начало (0,0) обозначено черной точкой.
| Горизонтальный сдвиг (m=1.25) | Горизонтальный поворот | Сжатие (r=3/2) | Масштабирование (3/2) | Поворот (π/6R = 30°) |
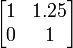 | 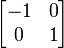 | 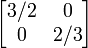 | 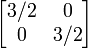 | 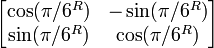 |
 |  |  | 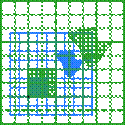 | 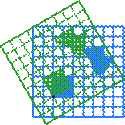 |
Связанные понятия
Линейные комбинации
В векторном пространстве линейной комбинацией векторов 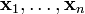 называется вектор
называется вектор
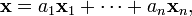
где 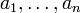 — коэффициенты разложения:
— коэффициенты разложения:
- если все коэффициенты равны нулю, то такая комбинация называется тривиальной,
- если же хотя бы один коэффициент отличен от нуля, то такая комбинация называется нетривиальной.
Это позволяет описать произведение 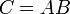 матриц
матриц  и
и 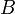 терминах линейных комбинаций:
терминах линейных комбинаций:
- столбцы матрицы
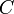 — это линейные комбинации столбцов матрицы
— это линейные комбинации столбцов матрицы  с коэффициентами, взятыми из матрицы
с коэффициентами, взятыми из матрицы 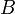 ;
; - строки матрицы
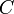 — это линейные комбинации строк матрицы
— это линейные комбинации строк матрицы 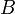 с коэффициентами, взятыми из матрицы
с коэффициентами, взятыми из матрицы  .
.
Линейная зависимость
Если какой-либо вектор можно представить в виде линейной комбинации, то говорят о линейной зависимости данного вектора от элементов комбинации.
Точнее, говорят так: некоторая совокупность элементов векторного пространства называется линейно зависимой, если существует равная нулю линейная комбинация элементов данной совокупности или
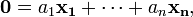
где не все числа 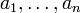 равны нулю; если такой нетривиальной комбинации не существует, то данная совокупность векторов называется линейно независимой.
равны нулю; если такой нетривиальной комбинации не существует, то данная совокупность векторов называется линейно независимой.
Линейная зависимость векторов означает, что какой-то вектор заданной совокупности линейно выражается через остальные векторы.
Каждая матрица представляет собой совокупность векторов (одного и того же пространства). Две такие матрицы — две совокупности. Если каждый вектор одной совокупности линейно выражается через векторы другой совокупности, то на языке теории матриц этот факт описывается при помощи произведения матриц:
- если строки матрицы
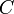 линейно зависят от строк матрицы
линейно зависят от строк матрицы 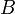 , то
, то 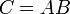 для некоторой матрицы
для некоторой матрицы  ;
; - если столбцы матрицы
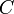 линейно зависят от столбцов другой матрицы
линейно зависят от столбцов другой матрицы  , то
, то 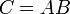 для некоторой матрицы
для некоторой матрицы 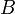 .
.
Ранг матрицы
Количество линейно независимых строк матрицы называют строчным рангом матрицы, а количество линейно независимых столбцов матрицы называют столбцовым рангом матрицы. В действительности, оба ранга совпадают. Их общее значение и называется рангом матрицы.
Другой эквивалентный данному подход заключается в определении ранга матрицы, как максимального порядка отличного от нуля минора матрицы.
Свойства
Матричные операции
Сложение и вычитание допускается только для матриц одинакового размера.
Существует нулевая матрица 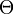 такая, что её прибавление к другой матрице A не изменяет A, то есть
такая, что её прибавление к другой матрице A не изменяет A, то есть
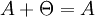
Все элементы нулевой матрицы равны нулю.
Возводить в степень можно только квадратные матрицы.
- Ассоциативность сложения:
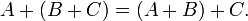
- Коммутативность сложения:
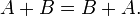
- Ассоциативность умножения:
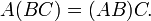
- Вообще говоря, умножение матриц некоммутативно:
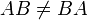 . Используя это свойство, вводят коммутатор матриц.
. Используя это свойство, вводят коммутатор матриц. - Дистрибутивность умножения относительно сложения:
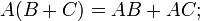
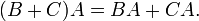
- С учётом упомянутых выше свойств, матрицы образуют кольцо относительно операций сложения и умножения.
- Свойства операции транспонирования матриц:
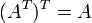
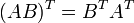
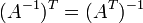 , если обратная матрица
, если обратная матрица 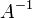 существует.
существует.
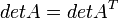
Примеры
Основная статья: Список матриц
Матрица линейного оператора
Матрица линейного оператора — матрица, выражающая линейный оператор в некотором базисе. Для того, чтобы ее получить, необходимо подействовать оператором на векторы базиса и координаты полученных векторов (образов базисных векторов) записать в столбцы матрицы.
Матрица оператора аналогична координатам вектора. При этом действие оператора на вектор равносильно умножению матрицы на столбец координат этого вектора в том же базисе.
Выберем базис 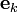 . Пусть
. Пусть  — произвольный вектор. Тогда его можно разложить по этому базису:
— произвольный вектор. Тогда его можно разложить по этому базису:
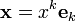 ,
,
где 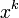 — координаты вектора
— координаты вектора 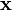 в выбранном базисе.
в выбранном базисе.
Здесь и далее предполагается суммирование по немым индексам.
Пусть 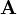 — произвольный линейный оператор. Подействуем им на обе стороны предыдущего равенства, получим
— произвольный линейный оператор. Подействуем им на обе стороны предыдущего равенства, получим
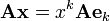 .
.
Вектора 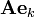 также разложим в выбранном базисе, получим
также разложим в выбранном базисе, получим
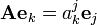 ,
,
где 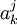 —
— 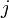 -я координата
-я координата 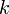 -го вектора из
-го вектора из 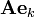 .
.
Подставим разложение в предыдущую формулу, получим
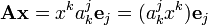 .
.
Выражение 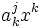 , заключённое в скобки, есть ни что иное, как формула умножения матрицы на столбец, и, таким образом, матрица
, заключённое в скобки, есть ни что иное, как формула умножения матрицы на столбец, и, таким образом, матрица 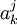 при умножении на столбец
при умножении на столбец 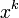 даёт в результате координаты вектора
даёт в результате координаты вектора 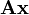 , возникшего от действия оператора
, возникшего от действия оператора 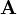 на вектор
на вектор 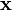 , что и требовалось получить.
, что и требовалось получить.
 Комментарий: Если в полученной матрице поменять местами пару столбцов или строк, то мы, вообще говоря, получим уже другую матрицу, соответствующую тому же набору базисных элементов
Комментарий: Если в полученной матрице поменять местами пару столбцов или строк, то мы, вообще говоря, получим уже другую матрицу, соответствующую тому же набору базисных элементов 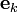 . Иными словами, порядок базисных элементов предполагается жёстко упорядоченным.
. Иными словами, порядок базисных элементов предполагается жёстко упорядоченным.
Матрицы в теории групп
Матрицы играют важную роль в теории групп. Они используются при построении общих линейных групп, специальных линейных групп, диагональных групп, треугольных групп, унитреугольных групп.
Конечную группу (в частности, симметрическую) можно (изоморфно) промоделировать матрицами перестановок (содержащими только "0" и "1"),
например, для 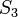 :
: 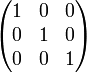 ,
, 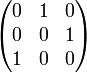 ,
, 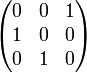 ,
, 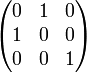 ,
, 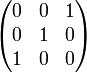 ,
, 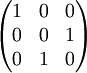 .
.
Поле 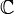 комплексных чисел может быть (изоморфно) промоделировано над полем
комплексных чисел может быть (изоморфно) промоделировано над полем 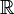 вещественных чисел:
вещественных чисел:
для 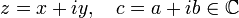 матричные аналоги
матричные аналоги 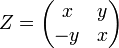 ,
, 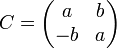 , где
, где 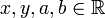 ;
;
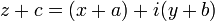 соответствует
соответствует 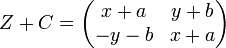 ;
;
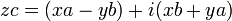 соответствует
соответствует 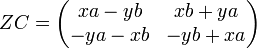 ;
;
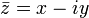 соответствует
соответствует 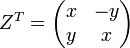 ;
;
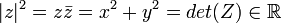 ;
;
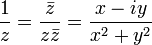 при
при  соответствует
соответствует 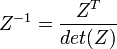 при
при 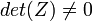 ;
;
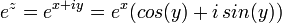 соответствует
соответствует 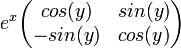 .
.
В частности, для 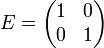 ,
, 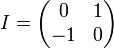
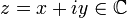 соответствует
соответствует 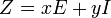 ,
,
где 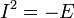 .
.
Замечание. Модель имеет автоморфизм 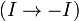 , т.е.
, т.е. 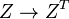
Тело кватернионов 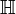 может быть (изоморфно) промоделировано над полем
может быть (изоморфно) промоделировано над полем  вещественных чисел:
вещественных чисел:
для 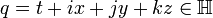 матричный аналог
матричный аналог 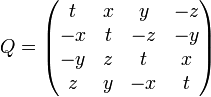 , где
, где  .
.
Для того, чтобы кватерниону 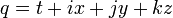 соответствовала матрица
соответствовала матрица 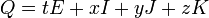 ,
,
где 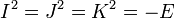 ,
, 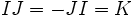 ,
, 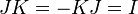 ,
, 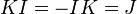 ,
,
можно ввести базисные элементы
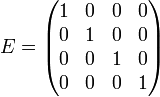 ,
, 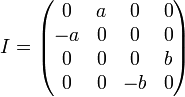 ,
, 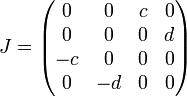 ,
, 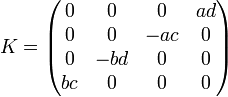 .
.
Параметры должны удовлетворять условиям: 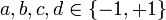 и
и 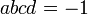 .
.
Существует 8 решений (8 представлений).
См. также
- Норма матрицы
- Определитель матрицы
- Собственные векторы, значения и пространства
- Массив — тип данных в программировании, соответствующий матрице (многомерность достигается вложенными массивами).
- Разрежённый массив — компьютерная форма представления матриц со множеством нулей.
- Линейные матричные неравенства — аппарат для решения задач синтеза законов управления.
- Лямбда-матрица
- Жорданова нормальная форма
- Список матриц
Примечания
- ↑ Под треугольными матрицами сейчас понимают матрицы, ненулевые элементы которых заполняют в таблице матрицы треугольную область, остальные же элементы - нули.
- ↑ Этот изоморфизм полностью задается выбором базиса в линейном пространстве: при фиксированном базисе изоморфизм фиксирован и таким образом реализована взаимная однозначность соответствия матриц операторам. Это не означает того, что такой изоморфизм в принципе единственный: в другом базисе тем же линейным операторам будут соответствовать другие матрицы (тоже взаимно однозначно при фиксации этого нового базиса).
- ↑ Даан-Дальмедико А., Пейффер Ж. Пути и лабиринты. Очерки по истории математики: Пер. с франц. — М.: Мир, 1986. — С. 397.
- ↑ Формально в этом определении всё симметрично, и можно было бы поменять "основной" и дуальный базис местами (они оба просто взаимно дуальны), однако принято именно описанное соглашение.
История
Впервые матрицы упоминались ещё в древнем Китае, называясь тогда «волшебным квадратом». Основным применением матриц было решение линейных уравнений. Также волшебные квадраты были известны чуть позднее у арабских математиков, примерно тогда появился принцип сложения матриц. После развития теории определителей в конце 17-го века, Габриэль Крамер начал разрабатывать свою теорию в 18-ом столетии и опубликовал «правило Крамера» в 1751 году. Примерно в этом же промежутке времени появился «метод Гаусса». Теория матриц начала своё существование в середине XIX века в работах Уильяма Гамильтона и Артура Кэли. Фундаментальные результаты в теории матриц принадлежат Вейерштрассу, Жордану, Фробениусу. Термин «матрица» ввел Джеймс Сильвестр в 1850 г.[3]
Определение
Пусть есть два конечных множества 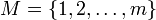 и
и 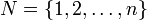 , где
, где 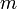 и
и 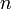 - натуральные числа.
- натуральные числа.
Назовём матрицей размера 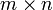 (читается
(читается 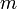 на
на 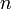 ) с элементами из некоторого кольца или поля
) с элементами из некоторого кольца или поля 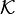 отображение вида
отображение вида
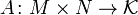 .
.
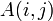 называется элементом матрицы, находящимся на пересечении
называется элементом матрицы, находящимся на пересечении 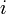 -той строки и
-той строки и 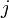 -ого столбца;
-ого столбца;
-
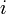 -ая строка матрицы состоит из элементов вида
-ая строка матрицы состоит из элементов вида 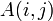 , где
, где 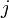 пробегает всё множество
пробегает всё множество 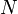 ;
; -
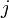 -ый столбец матрицы состоит из элементов вида
-ый столбец матрицы состоит из элементов вида 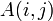 , где
, где 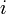 пробегает всё множество
пробегает всё множество 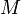 .
.
Если индекс 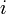 пробегает множество
пробегает множество 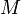 , а
, а 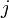 пробегает множество
пробегает множество 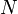 , то совокупность элементов
, то совокупность элементов 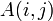 полностью определяет матрицу.
полностью определяет матрицу.
Таким образом, матрица размера 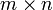 состоит в точности из
состоит в точности из
-
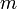 строк (по
строк (по 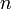 элементов в каждом)
элементов в каждом) - и
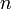 столбцов (по
столбцов (по 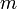 элементов в каждом)
элементов в каждом) - или
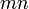 элементов.
элементов.
В соответствии с этим
- каждую строку матрицы можно интерпретировать как вектор в
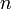 -мерном координатном пространстве
-мерном координатном пространстве 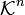 ;
; - каждый столбец матрицы — как вектор в
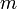 -мерном координатном пространстве
-мерном координатном пространстве 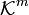 .
.
Сама матрица естественным образом интерпретируется как вектор в пространстве 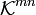 , имеющем размерность
, имеющем размерность 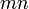 . Это позволяет ввести покомпонентное сложение матриц и умножение матрицы на число (см. ниже); что касается матричного умножения, то оно существенным образом опирается на прямоугольную структуру матрицы.
. Это позволяет ввести покомпонентное сложение матриц и умножение матрицы на число (см. ниже); что касается матричного умножения, то оно существенным образом опирается на прямоугольную структуру матрицы.
Если у матрицы количество строк 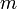 совпадает с количеством столбцов
совпадает с количеством столбцов 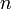 , то такая матрица называется квадратной, а число
, то такая матрица называется квадратной, а число 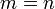 называется размером квадратной матрицы или её порядком.
называется размером квадратной матрицы или её порядком.
Обозначения
Обычно матрицу обозначают заглавной буквой латинского алфавита: пусть
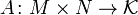 ,
,
тогда  — матрица, которая интерпретируется как прямоугольный массив элементов поля
— матрица, которая интерпретируется как прямоугольный массив элементов поля 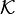 вида
вида 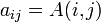 , где
, где
- первый индекс означает индекс строки:
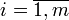 ;
; - второй индекс означает индекс столбца:
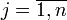 ;
;
таким образом, 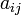 — элемент матрицы
— элемент матрицы  , находящийся на пересечении
, находящийся на пересечении 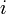 -той строки и
-той строки и 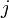 -того столбца. В соответствии с этим принято следующее компактное обозначение для матрицы размера
-того столбца. В соответствии с этим принято следующее компактное обозначение для матрицы размера 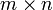 :
:
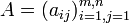
или просто:
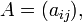
если нужно просто указать обозначение для элементов матрицы.
Иногда, вместо 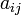 , пишут
, пишут 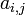 , чтобы отделить индексы друг от друга и избежать смешения с произведением двух чисел.
, чтобы отделить индексы друг от друга и избежать смешения с произведением двух чисел.
Если необходимо дать развёрнутое представление матрицы в виде таблицы, то используют запись вида

Можно встретить как обозначения с круглыми скобками «(…)», так и обозначения с квадратными скобками «[…]». Реже можно встретить обозначения с двойными прямыми линиями "||…||").
Поскольку матрица состоит из строк и столбцов, для них используются следующие обозначения:
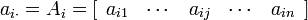 — это
— это 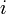 -тая строка матрицы
-тая строка матрицы  ,
,
а
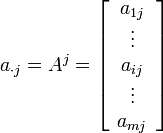 — это
— это 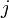 -тый столбец матрицы
-тый столбец матрицы  .
.
Таким образом, матрица обладает двойственным представлением — по строкам:
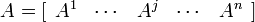
и по столбцам:
 .
.
Такое представление позволяет формулировать свойства матриц в терминах строк или в терминах столбцов.
Транспонированная матрица
С каждой матрицей 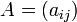 размера
размера 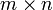 связана матрица
связана матрица 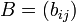 размера
размера
