Относительная частота события

Пусть проведено n испытаний в одних и тех же условиях. частотой события называется количество появлений события А в n испытаниях. Обозначают частоту события буквой m. Отношение частоты события к общему количеству всех проведенных испытаний называется относительной частотой события.

Относительная частота события А определяется формулой .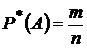

В классическом определении вероятностей не требуется, чтобы испытания проводились в действительности; в определении относительной частоты предполагается, что испытания были проведены.

Если испытания проводились в одинаковых условиях, и число испытаний было достаточно велико, то относительная частота обнаруживает свойство устойчивости: В различных опытах относительная частота изменяется мало, колеблясь около некоторого постоянного числа. Это постоянное число есть вероятность появления события.

Статистической вероятностью события Ав испытании называется число Р(А), около которого группируются значения относительной частоты при большом количестве испытаний n.

Пример 6.1.В ящике 8 пронумерованных шаров с номерами № 1, № 2, ..., № 8. Вынули один шар. Какова вероятность того, что номер вынутого шара не превышает 8?

Решение.Пусть событие А - вынули шар с номером не больше 8. Данное событие достоверное, следовательно, вероятность P(A)=1.

Пример 6.2. Брошены две игральные кости. Найти вероятность того, что сумма очков на выпавших гранях – четная, причем на грани хотя бы одной из костей появится шестерка.

Решение. На выпавшей грани «первой» игральной кости может появиться одно очко, два очка,..., шесть очков. Аналогичные шесть элементарных исходов возможны при бросании «второй» кости. Каждый из исходов бросания «первой» кости может сочетаться с каждым из исходов бросания «второй». Таким образом, общее число возможных элементарных исходов испытания равно 6·6=36.

Эти исходы единственно возможны, и, в силу симметрии костей, равновозможные.

Благоприятствующими интересующему нас событию являются следующие пять исходов:

1) 6, 2; 6+2=8, 4) 2, 6; 2+6=8,

2) 6, 4; 6+4=10, 5) 4, 6; 4+6= 10.

3) 6, 6; 6+6=12,

Искомая вероятность равна отношению числа исходов, благоприятствующих событию, к числу всех возможных элементарных исходов: .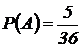

Пример 6.3. По цели произвели 25 выстрелов, зарегистрировали 23 попадания. Найти относительную частоту попадания в цель.

Решение. Число проведенных экспериментов (выстрелы по мишени) 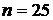, частота попадания в цель 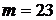. Относительная частота: .

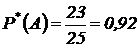Пример 6.4. Монета брошена пять раз. Орел выпал два раза. Каковы вероятность и относительная частота выпадения орла?

Решение. Вероятность впадения орла есть 0,5 (из двух возможных исходов при подбрасывании монеты выпадению орла благоприятствует один), а относительная частота выпадения орла есть 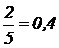(событие наступило два раза в пяти испытаниях).

Самостоятельная работа студентов на занятии

1. В ящике 10 перенумерованных шаров с номерами № 1, № 2, ..., № 10. Вынули один шар. Какова вероятность того, что номер вынутого шара не превышает 10?

2. В урне 15 шаров: 5 белых и 10 черных. Какова вероятность вынуть из урны синий шар?

3. В урне 12 шаров: 3 белых, 4 черных и 5 красных. Какова вероятность вынуть из урны черный шар

4. В урне 20 шаров с номерами № 1, № 2, № 3, .... № 20. Какова вероятность вынуть шар с № 37?

5. В лотерее 2000 билетов. На один билет падает выигрыш 100 руб., на четыре билета – выигрыш по 60 руб., на десять билетов – выигрыш по 20 руб., на двадцать билетов – выигрыш по 10 руб., на 165 билетов – выигрыш по 5 руб., на 400 билетов – выигрыш по 1 руб. Остальные билеты невыигрышные. Какова вероятность выиграть по билету не меньше 10 руб.?

6. Монета подброшена два раза. Какова вероятность того, что оба раза выпадает орел?

7. Брошены две игральные кости. Найти вероятность того, что сумма очков на выпавших гранях равна семи.

8. В партии из 100 деталей отдел технического контроля обнаружил 5 нестандартных деталей? Чему равна относительная частота появления нестандартной детали?

9. Набирая номер телефона, абонент забыл одну последнюю цифру. Найти вероятность того, что абонент набрал правильный номер.

10. По данным автопредприятия на 1000 рейсов автобусов в 50 случаются поломки. Найти вероятность поломки одного автобуса.

11. При стрельбе из винтовки относительная частота попадания в цель оказалась равной 0,85. Найти число попаданий, если всего было произведено 120 выстрелов.

12. В лотерее разыгрываются 100 билетов с номерами от 1 до 100. Найти вероятность того, что номер первого наудачу извлеченного билета не содержит цифры два.

Защита презентаций по теме: «Применение математического анализа при решении задач физики, химии, фармации».

Задание на дом

Практика

1. Из колоды карт наудачу выбирают одну карту. Найти вероятность того, что эта карта пиковой масти.

2. Из тщательно перемешанного набора 28 костей домино наудачу извлечена кость. Найти вероятность того, что вторую кость можно приставить к первой, если первая кость оказалась: а) дублем; б) не дублем.

3. Брошены две игральные кости. Найти вероятность того, что

- сумма выпавших очков равна восьми, а разность – четырем;

- сумма выпавших очков равна пяти, а произведение – четырем.

4. Среди 500 ампул, проверенных на герметичность, оказалось 10 ампул с трещинами. Определить относительную частоту появления ампул, имеющих трещины.

5. Среди 1000 новорожденных оказалось 517 мальчиков. Найти относительную частоту рождения мальчиков.

Теория

1. Лекция по теме «Теорема сложения вероятностей для несовместных событий. Случайные величины. Числовые характеристики дискретной случайной величины».

2. Занятие 7 данного методического пособия.

3. Павлушков И.В. и другие стр. 232-233, 247-249, 256-261