Вторая производная и ее физический смысл

Пусть ф-ция y=f(x) непрерывна в окрестности критической точки 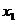и I производная в этой точке =0. Если II производная данной ф-ции также непрерывна в окрестности точки 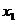, то справедлива теорема- если в критической точке 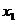первая производная =0, то ф-ция будет иметь максимум в точке 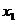,если выполняется условие 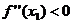-max, ф-ция будет иметь в данной точке минимум, если выполняется условие 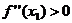-min

Примечание:если вторая производная в точке 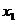=0, то теорема не дает ответа на вопрос о наличие экстремума в этой точке.в данном случае исследование нужно проводить с помощью I производной.

Алгоритм исследования ф-ции по второй производной

1)находим D(y)

2)находят производную данной ф-ции

3)приравнивают полученную производную к нулю и находят критические точки.

4)находят II производную данной ф-ции

5)подставляют полученные критические точки поочередно во II производную. Если при подстановке II производная положительна, то данная точка-минимум ф-ции. Если при подстановке II производная отрицательна, то данная точка-максимум ф-ции.

6)вычесляют значение ф-ции в экстремальных точках путем их подстановки в условие.

Выпуклость кривой. Точки перегиба.

Если в заданном промежутке II производная отрицательна, то кривая выпуклая на этом промежутке.
правило нахождения интервалов выпуклости и вогнутости

1) находят D(y)

2) вычесл.производную дан. ф-ции

3)вычесл. Вторую производную

4) приравнивают вторую производную к нулю и находят критические точки II рода.

5)получен.точками разбивают D(y) на интервалы и находят знак второй производной в каждом интервале путем подстановки любых чисел из интервала,кроме критических точек во II производную.

6)если на интервале II производная положительна,то ф-ция вогнута на этом интервале. Если II производная отрицательна, то ф-ция выпуклая на этом интервале.

Исследование ф-ции на точки перегиба

Точкой перегиба кривой наз. Такая точка,которая отделяет выпуклую часть кривой от вогнутой

(маленький рисунок)

Теорема. Признак существования точки перегиба.

Если II производная ф-ции y=f(x) непрерывна и меняет знак при переходе через критическую точку 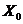, то данная точка- точка перегиба графика ф-ции y=f(x)

Правило нахождения точек перегиба.

1)

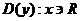
2) 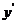данной ф-ции

3) 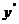данной ф-ции

4) приравнивают 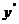к нулю и находят критич.точки II рода

5) получ. точками разбивают D(y) на интервалы и опред. знак 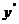в каждом интервале

6) если при переходе через критич. точку вторая производная меняет знак, то данная точка-точка перегиба графика ф-ции

7)находят знач.ф-ции в точках перегиба путем их подстановки в условие.

Полное исследование ф-ции

1)находят область определен.ф-ции

2)исследуют ф-цию на четность или нечетность

3)опред. точки пересечен. Графика ф-ции с осями координат(если возможно)

4)вычесл. Первую производную ф-ции

5)находят еритические точки и исследуют ф-цию на монотонность или экстремумы

6)находят вторую производную ф-ции

7)находят критич. точки второго рода и исследуют ф-цию на выпуклость/вогнутость и точки перегиба

8)используя рез-ты всех исследований соединяют получ. точки плавной кривой