Правила дифференцирования, производная сложной и обратной функции. Производные элементарных функций.
431. Правила дифференцирования, производная сложной и обратной функции.
Если функции 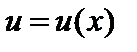 и
и 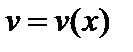 имеют производныев точке x, то сумма, разность, произведение и частное этих функций также имеют производную в этой точке (частное при условии, что
имеют производныев точке x, то сумма, разность, произведение и частное этих функций также имеют производную в этой точке (частное при условии, что 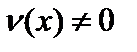 ) и справедливы следующие формулы:
) и справедливы следующие формулы:
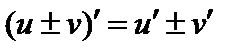 ,
, 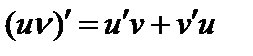 ,
, 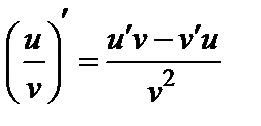 . (1)
. (1)
Производная обратной функции.
Утверждение 1. Если функция 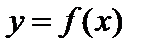 строго монотонна и непрерывна в некоторой окрестности точки
строго монотонна и непрерывна в некоторой окрестности точки 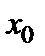 , имеет производную в точке
, имеет производную в точке 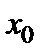 и
и 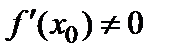 , то обратная функция
, то обратная функция 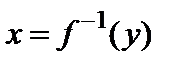 имеет производную в соответствующей точке
имеет производную в соответствующей точке 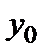 ,
, 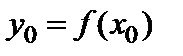 , причем
, причем 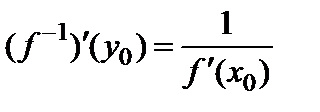 .
.
Производная сложной функции.
Утверждение 1. Если функция 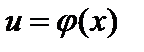 имеет в точке
имеет в точке 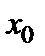 производную, а функция
производную, а функция 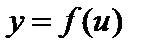 имеет в соответствующей точке
имеет в соответствующей точке 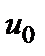
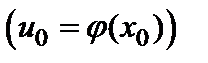 производную
производную 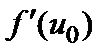 , то сложная функция
, то сложная функция 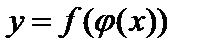 имеет производную в точке
имеет производную в точке 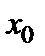 и справедлива следующая формула:
и справедлива следующая формула:
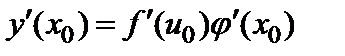 . (1)
. (1)
432. Производные элементарных функций.
Производная постоянной, степенной, тригонометрических и показательной функций.
а) Пусть 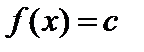 . Тогда
. Тогда 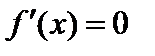 , т.е.
, т.е. 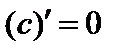 .
.
б) Пусть 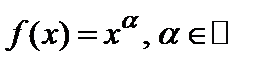 . Тогда
. Тогда 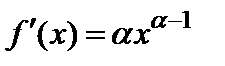 , т.е.
, т.е.
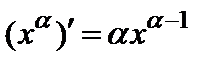 . (2)
. (2)
в) Производная функции 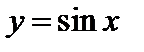 выражается формулой
выражается формулой 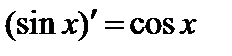 .
.
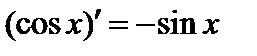 .
.
Из полученных формул и правила дифференцирования частного имеем:
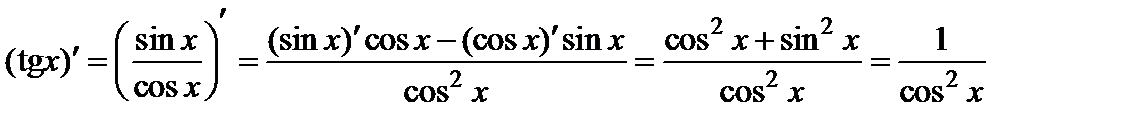 ,
,
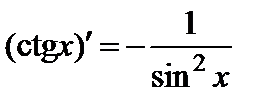 . ☐
. ☐
г) С помощью второго замечательного предела можно показать, что
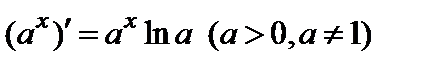 . (3)
. (3)
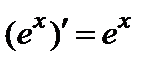 .
.
Логарифмическая производная.Предположим, что
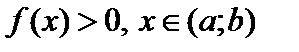 .
.
Рассмотрим функцию 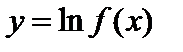 . Дифференцируя эту функцию как сложную, где
. Дифференцируя эту функцию как сложную, где 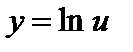 ,
, 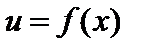 , получим
, получим
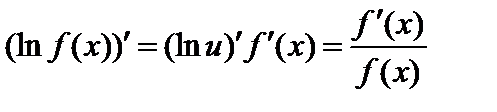 . (2)
. (2)
Производная от логарифма функции называется логарифмической производной этой функции, а последовательное применение операции логарифмирования, а затем дифференцирования называется логарифмическим дифференцированием.
С помощью этого метода найдем производную показательно-степенной функции 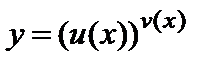 , где
, где  – функции, имеющие в точке x производные и
– функции, имеющие в точке x производные и  . Применяя формулу (2), получим
. Применяя формулу (2), получим
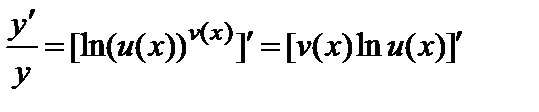 .
.
В правой части имеем производную произведения:
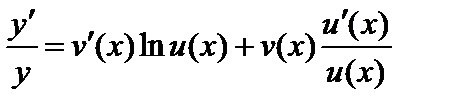 .
.
Следовательно,
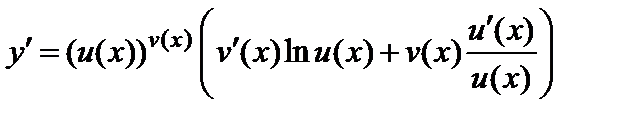 . (3)
. (3)
Производная логарифмической и обратных тригонометрических функций.
а) Производная функции 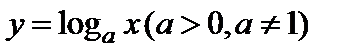 выражается формулой
выражается формулой 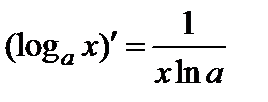 .
.
б) Производная функции 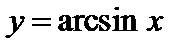 выражается формулой
выражается формулой
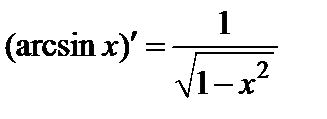 .
.
Корень взят со знаком плюс, так как 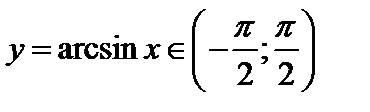 и
и 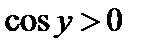 . □
. □
А также:
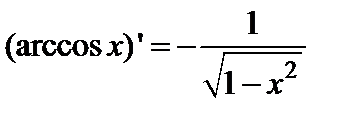 , (4)
, (4)
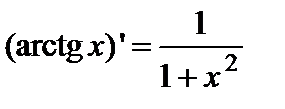 , (5)
, (5)
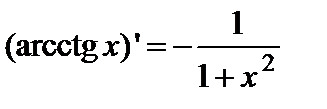 . (6)
. (6)
Дифференцирование функций, заданных параметрически и неявно. Производные и дифференциалы высших порядков.
441. Дифференцирование функций, заданных параметрически и неявно.
Неявно заданная функция
Если функция задана уравнением у=ƒ(х), разрешенным относительно у, то функция задана в явном виде (явная функция).Под неявным заданием функции понимают задание функции в виде уравнения F(x;y)=0, не разрешенного относительно у.Всякую явно заданную функцию у=ƒ (х) можно записать как неявно заданную уравнением ƒ(х)-у=0, но не наоборот.Не всегда легко, а иногда и невозможно разрешить уравнение относительно у (например, у+2х+cosy-1=0 или 2у-х+у=0).Если неявная функция задана уравнением F(x; у)=0, то для нахождения производной от у по х нет необходимости разрешать уравнение относительно у: достаточно продифференцировать это уравнение по x, рассматривая при этом у как функцию х, и полученное затем уравнение разрешить относительно у'.Производная неявной функции выражается через аргумент х и функцию у.
