Линейные уравнения второго порядка с постоянными коэффициентами

1. Однородные линейные уравнения с постоянными коэффициентами

Рассматриваем уравнение 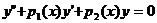, считая в нем коэффициенты

р₁, р₂ постоянными. Это уравнение имеет ФСР 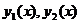, состоящую из степенных, показательных и тригонометрических функций. Соответсвующее ей общее решение 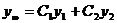определено в области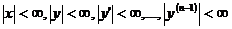

ФСР строится по методу Эйлера. В этом случае частное решение однородного уравнения ищем в виде 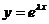, где λ – некоторое неизвестное число (вещественное или комплексное). Для его нахождения составляют характеристическое уравнение .

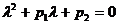Структура общего решения зависит от вида корней характеристического уравнения.

а) Корни 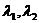характеристического уравнения вещественны и различны. ФСР в этом случае имеет вид 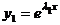, , 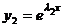а общее решение .

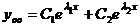б) Корень 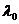характеристического уравнения вещественнен и имеет кратность 2. ФСР имеет вид 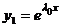, , 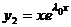а общее решение .

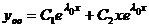в) Корни характеристического уравнения комплексно сопряженные: 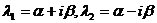. В этом случае ФСР имеет вид 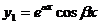, , 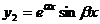а общее решение .

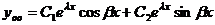Пример 12.25.

Найдем общее решение дифференциального уравнения .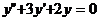

Характеристическое уравнение имеет вид, 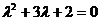, откуда 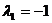, 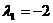- вещественные различные числа. Общее решение .

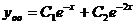Пример 12.26.

Найдем общее решение дифференциального уравнения .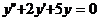

Характеристическое уравнение 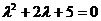имеет корни 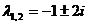. Следовательно, функции 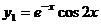, 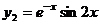составляют ФСР, а общее решение имеет вид .

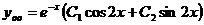2. Неоднородные линейные уравнения с постоянными коэффициентами

В некоторых случаях для неоднародного линейного уравнения с постоянными коэффициентами удается найти частное решение у_ч методом неопределённых коэффициентов, когда правая часть уравнения имеет специальный вид.

Укажем эти случаи и соответствующие им виды частных решений.

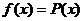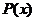1) Пусть , где - многочлен от х; в частности, это может быть число А≠ 0, тогда:

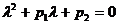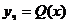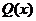а) если число 0 не является корнем характеристического уравнения , то частное решение можно найти в виде , где - многочлен той же степени, что и 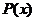, но с неопределенными коэффициентами;

б) если 0 есть корень характеристического уравнения кратности k=1,2, то .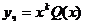

2) Пусть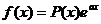

а) если число а не является корнем характеристического уравнения, то .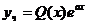

б) если а – корень кратности k=1,2, то .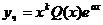

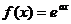
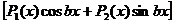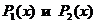3) Пусть , где - многочлены от х.

Эти многочлены, в частности, могут быть постоянными числами, и один из них может быть тождественно равен 0.

Пусть т есть наивысшая из степеней многочленов 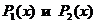, тогда:

а) если число а+ib не является корнем характеристического уравнения, то

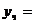
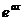
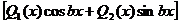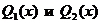, где - многочлены степени т с неопределенными коэффициентами;

б) если а+ib есть корень (простой) характеристического уравнения, то .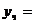

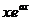
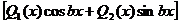4) Пусть 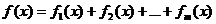, где 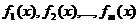- функции вида, рассмотренного в пп. 1)-3). Если 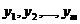есть частные решения, соответствующие уравнениям с правыми частями 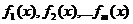, то 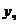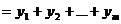является частным решением исходного уравнения.

Пример 12.27.

Решим дифференциальное уравнение .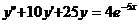

Характеристическое уравнение 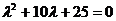имеет двукратный корень 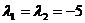, поэтому .

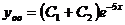Правая часть 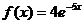, 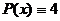. Так как 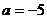является корнем характеристического уравнения кратности 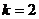, то частное решение ищем в виде 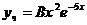. Имеем , .

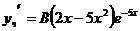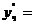
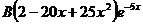Подставляя 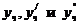в исходное уравнение, получим 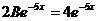, откуда В= 2 и .

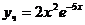Общее решение исходного уравнения .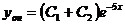

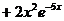Пример 12.28.

Найдем общее решение дифференциального уравнения .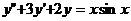

Характеристическое уравнение 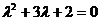имеет корни 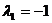, 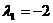- вещественные различные числа. Общее решение .

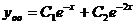Правая часть 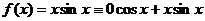. Число 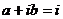не является корнем характеристического уравнения.

Для определения частного решения используем рекомендацию пункта 3).

Определим m 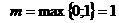, и таким образом,

.

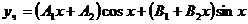Найдем 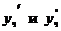и подставим 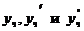в заданное уравнение.

Приравняв коэффициенты при функциях 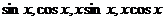в левой и правой частях уравнения, получим систему уравнений относительно :

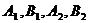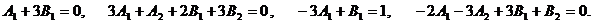
Решая систему, получим 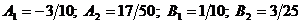, и значит, частное решение .

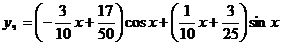Общее решение .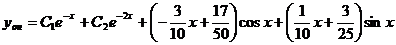

Пример 12.29.

Найдем общее решение дифференциального уравнения .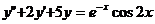

Характеристическое уравнение 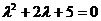имеет корни 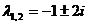, так что .

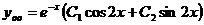Правая часть 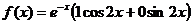и так как число 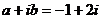является простым корнем характеристического уравнения, то частное решение надо искать в виде .

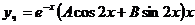Имеем ,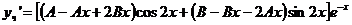

.

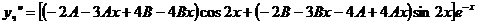Подставив 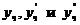в исходное уравнение и сокращая на 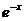, получим 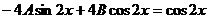, откуда 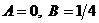и .

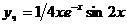Общее решение .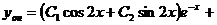

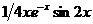Пример 12.30.

Решим дифференциальное уравнение .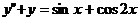

Найдем общее решение соответствующего однородного уравнения .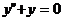

Имеем 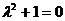, откуда .

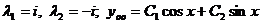Рассмотрим уравнение .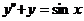

Так как число 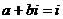является корнем характеристического уравнения, то частное решене ищется в виде .

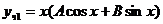Подставим 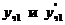в это неоднородное уравнение, откуда получим А = 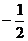, В = 0, у_ч1 = 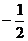xcosx.

Рассмотрим уравнение .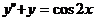

Число 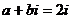не является корнем характеристического уравнения, следовательно, частное решение ищется в виде у_ч2 = С cos2x + D sin2x.

Подставим у_ч2 и у_ч2'' в соответствующее однородное уравнение, откуда получим С = 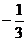, D = 0, у_ч2 = 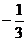xcos2x.

Используя принцип суперпозиции частных решений, получим общее решение исходного уравнения: у_он = С₁ cosx + C₂ sin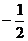x xcosx 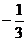xcos2x.