Экономический смысл интеграла.

С помощью определенного интеграла можно найти объем продукции u, произведенной за промежуток времени [0,T], если производительность производства описывается функцией y = f(t) на этом промежутке времени:

Пример 7.1.

Составить интегральную сумму S_n для функции на отрезке , разделив этот отрезок на равных частей и выбирая точки совпадающими с левыми концами частичных отрезков . Вычислить определённый интеграл как предел интегральных сумм (рис. 7.2).

Рис. 7.2 Рис. 7.3

Имеем и ,

откуда .

Следовательно,

=

Таким образом, а значит, .

Пример 7.2.

Найти площадь криволинейного треугольника, ограниченного дугой параболы , осью 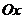и вертикальной прямой (рис. 7.3).

Разобьём основание криволинейного треугольника на равных частей с длиной .

Вычислив значение функции в начале каждого промежутка, будем иметь

.

Площади вписанных прямоугольников равны .

Суммируя, получим площадь ступенчатой фигуры

Пользуясь формулой суммы квадратов целых чисел

, находим .

Следовательно, (кв.ед.).

Пример 7.3.

С помощью определенного интеграла найдем дневную выработку u за восьмичасовой рабочий день, если производительность труда описывается формулой y= f (t) = а(-0,2t2 + 1,6t + 3), где tÎ[0,8] – время в часах, а – множитель размерности продукции.

Дневную выработку u можно выразить определенным интегралом

.

Свойства определённого интеграла

Свойство 1.

Если функции – интегрируемы на [a, b], то функции также интегрируемы на [a, b] и .

Свойство 2.

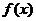Если функция интегрируема на [a, b], то функция , где – постоянная, также интегрируема на [a, b] и .

Свойство 3.

Для интегрируемой на [a, b] функции верно равенство: .

Следствие.

Для интегрируемой функции верно равенство .

Свойство 4.

Для любых чисел и интегрируемой функции 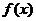выполняется

свойство аддитивности определённого интеграла относительно промежутка интегрирования: .

Свойство 5.

Если подынтегральная функция на отрезке интегрирования не меняет знака, то определённый интеграл сохраняет тот же знак, что и функция, то есть: если для всех , то .

Свойство 6. (Интегрирование неравенств).

Если для всех х и интегрируемы на [a, b], то верно неравенство .

Свойство 7.

Если функция интегрируема на [a, b], то верно неравенство

.

Свойство 8. (Оценка интеграла).

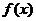Пусть функция интегрируема на [a, b] и для всех , тогда .

Свойство 9. (Теорема о среднем).

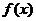Если функция непрерывна на [a, b], то существует точка , такая, что верно равенство .

Свойство 10. (Формула Ньютона–Лейбница).

Пусть 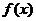непрерывна на , – какая-либо первообразная для неё, тогда .

Пример 7.4.

Оценим значение интеграла , не вычисляя его.

Найдём значения и для подынтегральной функции на отрезке [0, 2]. Для этого найдём стационарные точки.

откуда стационарной точкой на отрезке [0, 2] является точка ( ). Вычислим значения функции на границе отрезка: , следовательно, .

Таким образом получим 0,5∙2 ≤ ≤ 0,6∙2, или 1 ≤ ≤ 1,2.

Пример 7.5.

Вычислим определенный интеграл по формуле Ньютона-Лейбница.

Одна из первообразных подынтегральной функции равна , тогда

.